Matemática no Enem 2024: assuntos que mais caem na prova

Ei, vestibulando, sabia que, com um bom domínio de matemática básica e estatística, dá para garantir 20 questões no Exame Nacional do Ensino Médio (Enem)? Acredite se quiser, mais de 45% da prova é sobre esses conteúdos. E se você quer conhecer outros assuntos de Matemática que mais caem no Enem, conte com a gente!

A equipe do Aprova Total analisou as provas de cada componente nos últimos anos para identificar os temas que sempre aparecem. Percebemos que a incidência muda, mais ou menos, a cada sete anos. Por isso, o objetivo desse relatório é preparar você de forma certeira, indicando o melhor caminho para os estudos.

Em síntese, os 5 temas que mais aparecem nas questões de Matemática no Enem são:

1. Matemática básica
2. Estatística
3. Geometria espacial
4. Geometria plana
5. Funções

Veja o gráfico atualizado com os assuntos de Matemática que mais caem no Enem (com dados das provas de 2016 a 2023):

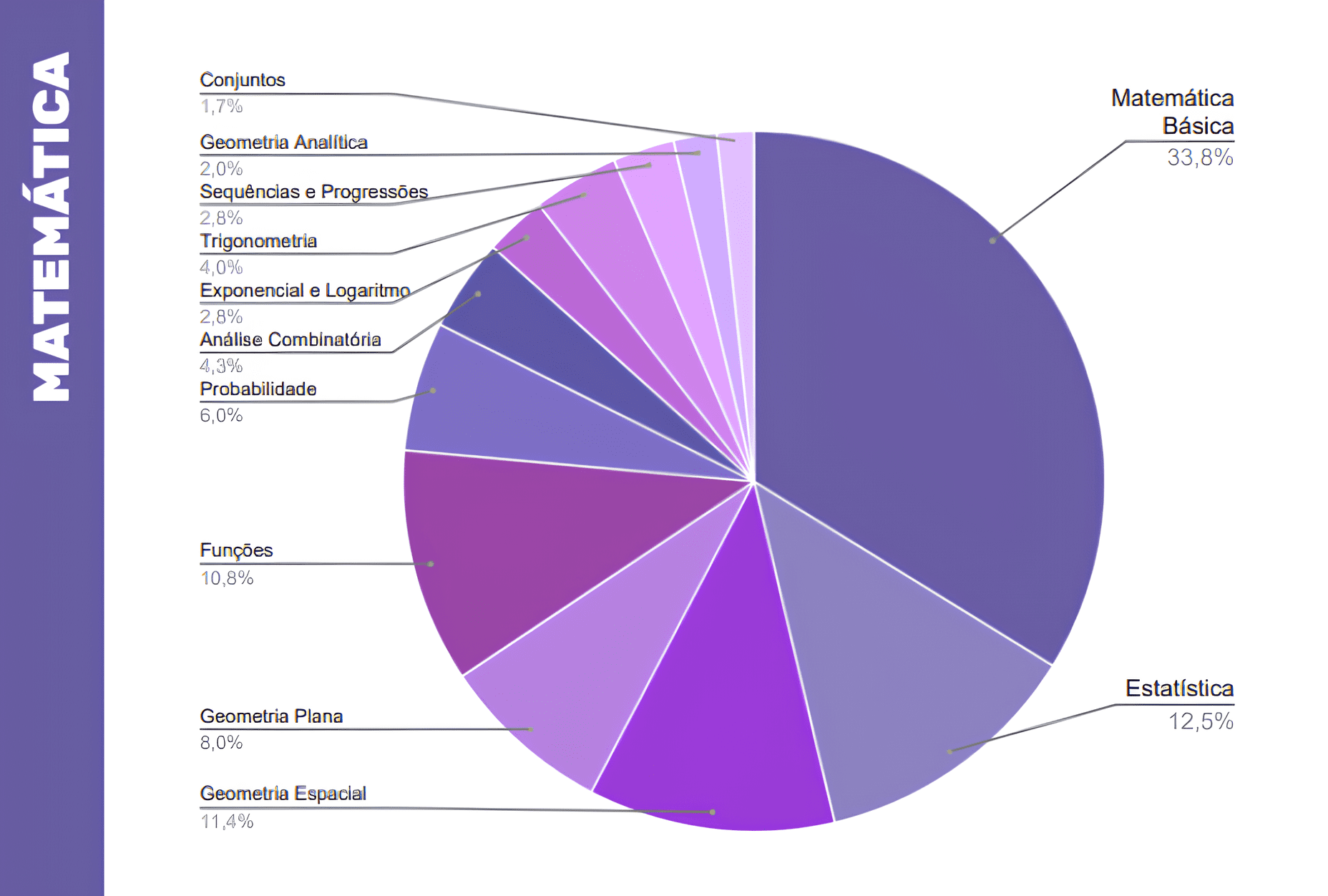
Viu só como, juntas, a matemática básica (33,8% de incidência) e a estatística (12,5% de incidência) contemplam quase metade das questões? Elas são seguidas de geometria espacial (11,4%), geometria plana (8%) e funções (10,8%).

Assuntos de Matemática que mais caem no Enem

A seguir, vamos entender melhor como os principais conteúdos costumam aparecer nas avaliações!

1. Matemática básica

A nossa campeã, que carrega o título há muitos anos é a matemática básica. E se você conhece um pouco dela, sabe que tem muita coisa nesse balaio de gato.

Dentre os conteúdos mais importantes para revisar, estão: números inteiros, frações, números decimais, potenciação, radiciação, transformação de unidades, equações do primeiro e segundo grau, porcentagem, razão e proporção, e, por último, mas não menos importante, a regra de três.

No Enem, em específico, vale a pena se dedicar às operações envolvendo números inteiros, frações, porcentagem e regra de três. São tópicos essenciais, não dá para fugir deles!

Regra de três

Para usar a regra de três, você precisa entender que ela é um método que ajuda a encontrar valores desconhecidos quando estamos trabalhando com grandezas diretamente ou inversamente proporcionais.

Mas o que são grandezas proporcionais? Para responder a essa pergunta, vamos voltar um pouco à razão e proporção. De forma intuitiva, razão é uma relação entre dois valores de uma mesma grandeza, enquanto a proporção indica igualdade entre duas razões.

Resumindo, duas grandezas são ditas proporcionais quando a variação em uma delas acarreta mudança na outra.

Exemplos de grandezas proporcionais
1 ➝ Número de pessoas construindo uma casa - Tempo para finalizar a construção
Quanto maior o número de pessoas trabalhando na construção, menor o tempo para finalizar a casa.

2 ➝ Quantidade de luz consumida na sua casa - Valor a pagar na sua conta de luz
Quanto menor for a quantidade de luz consumida, menor será o valor da conta de luz.

3 ➝ Tempo gasto na viagem - Distância percorrida de carro
Com o carro a uma velocidade constante, quanto maior for o tempo gasto na viagem, maior será a distância percorrida.

Para usar a regra de três, é essencial identificar se as grandezas oferecidas pelo problema são proporcionais ou inversamente proporcionais. Veja como diferenciá-las:

• Grandezas diretamente proporcionais: se uma das grandezas aumenta, a outra aumenta na mesma proporção. O mesmo vale para o caso de diminuir (entre os exemplos acima, os itens 2 e 3 são mostram grandezas diretamente proporcionais).
  
• Grandezas inversamente proporcionais: se uma das grandezas aumenta, a outra diminui na mesma proporção, e vice-versa (entre os exemplos acima, o item 1 apresenta uma grandeza inversamente proporcional).

Regra de três simples ou composta?

Se tivermos apenas duas grandezas diretamente ou inversamente proporcionais, chamamos de regra de três simples.

Exercício de regra de três simples

Para fazer um bolo de chocolate que renda 10 porções, são necessárias 4 colheres de sopa de chocolate em pó. Para fazer um bolo que renda 15 porções, devemos utilizar quantas colheres de sopa de chocolate?

Resposta:

O primeiro passo sempre é organizar as grandezas e identificar como elas se relacionam:

\(\text{Porcoes}\;\;\;\text{Colheres}\\ \uparrow 10\;\overline{\hspace{1cm}}\;\uparrow 4\\ \uparrow 15\;\overline{\hspace{1cm}}\;\uparrow x\)

Colocamos setas em sentidos iguais, porque, quanto mais porções de bolo queremos fazer, maior será a quantidade de colheres de chocolate em pó, ou seja, as grandezas são diretamente proporcionais. Equacionando a regra de três, temos:

\(\dfrac{10}{15}=\dfrac{4}{x}\)

\(10\cdot x=4\cdot 15\)

\(10\cdot x=60\)

\(x=6\)

Concluímos, então, que para fazer um bolo de chocolate que renda 15 porções, precisamos utilizar 6 colheres de sopa de chocolate em pó.

Na regra de três composta, a grande diferença é que se quer encontrar valores desconhecidos com mais de duas grandezas diretamente ou inversamente proporcionais entre si. 

Mas, cuidado! Quando temos mais de duas grandezas, no momento de estabelecer a relação de proporção direta ou inversa, é obrigatório usar como base de comparação aquela que possui o valor desconhecido.

Exercício de regra de três composta

Uma empreiteira disponibilizou 20 pedreiros para realizar certa obra. Eles trabalharam durante 15 dias, com um expediente de 6 horas diárias. A fim de agilizar o processo, a empreiteira encaminhou mais 5 pedreiros para ajudar. Supondo que os pedreiros aumentassem o expediente para 8 horas diárias, em quantos dias eles finalizariam a obra?

Resposta:

Assim como na regra de três simples, o primeiro passo sempre é organizar as grandezas e identificar como elas se relacionam:

\(\text{Pedreiros}\;\;\text{Dias}\;\;\text{Horas}\\20\;\overline{\hspace{1cm}}\;\uparrow15\;\overline{\hspace{1cm}}\;6\\25\;\overline{\hspace{1cm}}\;\uparrow x\;\overline{\hspace{1cm}}\;8\)

A partir da coluna em que há uma grandeza desconhecida (a quantidade de dias), vamos estabelecer relações com as demais. Relacionando os dias com a quantidade de pedreiros, se aumentarmos o número deles, diminuímos a quantidade de dias necessários.

Sendo assim, como as grandezas são inversamente proporcionais, colocamos uma flecha com sentido para baixo na coluna dos pedreiros:

\(\text{Pedreiros}\;\;\;\;\text{Dias}\;\;\;\;\text{Horas}\\\downarrow20\;\overline{\hspace{1cm}}\;\uparrow15\;\overline{\hspace{1cm}}\;6\\\downarrow25\;\overline{\hspace{1cm}}\;\uparrow x\;\overline{\hspace{1cm}}\;8\)

Por outro lado, relacionando os dias com as horas de trabalho, se mais horas forem trabalhadas diariamente, menos dias serão necessários para concluir a obra. Assim, como as grandezas são inversamente proporcionais, colocamos uma flecha com sentido para baixo na coluna das horas:

\(\text{Pedreiros}\;\;\;\;\text{Dias}\;\;\;\;\text{Horas}\\\downarrow20\;\overline{\hspace{1cm}}\;\uparrow15\;\overline{\hspace{1cm}}\;\downarrow6\\\downarrow25\;\overline{\hspace{1cm}}\;\uparrow x\;\overline{\hspace{1cm}}\;\downarrow8\)

Equacionando a regra de três, temos:

\(\dfrac{15}{x}=\dfrac{25}{20}\cdot \dfrac{8}{6}\)

\(\dfrac{15}{x}=\dfrac{200}{120}\)

\(200\cdot x=120\cdot 15\)

\(200\cdot x=1.800\)

\(x=\dfrac{1.800}{200}\)

\(x=9\)

Portanto, na segunda etapa da obra, os pedreiros finalizaram os trabalhos em 9 dias.

✨ Dica de ouro: sempre trabalhe com as grandezas em uma mesma unidade de medida ✨

2. Estatística

Entre os assuntos de Matemática que mais caem no Enem, podemos pensar na estatística como uma área que trata da coleta, da análise, da interpretação e da apresentação de massas de dados.

Esses dados costumam aparecer em meio a gráficos e tabelas, que frequentemente usam de medidas de tendência central ou medidas de dispersão para representá-los de maneira mais objetiva. No geral, as medidas de dispersão não caem no Enem, por isso, vamos aos demais tópicos.

Interpretação de gráficos e tabelas

Organizar dados com o auxílio de gráficos e tabelas é comum às Ciências da Natureza como um todo, então, para resolver os exercícios, é importante fazer uma leitura atenta do enunciado.

Procure identificar qual parte do gráfico ou da tabela é necessária para responder à questão, porque nem sempre todos os dados serão usados para a resolução. Vejamos alguns dos tipos de gráficos recorrentes e os principais contextos de uso:

Por fim, as tabelas ordenam informações em função das suas linhas e colunas, e é o contexto em que cada delas está inserida que determina como resolver o problema.

Medidas de tendência central (MTC)

Todo santo Enem, lá está ela, a tríade moda, média e mediana. É importante que você saiba diferenciá-las porque os valores podem variar de uma para outra.

• Moda: o elemento mais frequente, ou seja, o que mais se repete no conjunto de dados;
  
• Média: uma das medidas de tendência central mais utilizadas, que pode ser dividida em quatro tipos - aritmética simples, aritmética ponderada, geométrica e harmônica.
  
  As duas que aparecem com frequência são a média aritmética simples (soma de todos os dados divididos pelo número total de valores) e a média aritmética ponderada (soma os dados multiplicados pelos seus respectivos pesos e divididos pela soma de todos os pesos);
  
• Mediana: é o termo que, depois de organizar em ordem crescente a lista de dados, ocupa a posição central da lista. Caso o número de elementos do espaço seja par, você deve fazer a média aritmética dos termos centrais para encontrar a mediana.

A diferenciação teórica pode parecer complexa, por isso, vamos abordar um exemplo calculando um tipo de cada medida de tendência central, ok?

Exercício de medidas de tendência central

No reforço de Matemática, para praticar os conteúdos de medidas de tendência central, a professora pediu que cada estudante dissesse sua idade. Como estavam em setes pessoas, todos foram ao quadro e escreveram sua idade, resultando na seguinte lista:

Para calcular a média aritmética simples, é preciso somar todas as idades e dividir por 7, que é o número de estudantes no reforço. Então,

(16+17+16+18+16+17+19) ÷ 7 = 17 ➝ A média das idades é 17

Para calcular a moda, precisamos contar quantas vezes cada idade aparece. A forma mais comum de fazer isso é colocar as idades em uma tabela e registrar a frequência das idades:

Idade	Frequência
16	3
17	2
18	1
19	1

Veja que a idade 16 apareceu três vezes, mais do que as demais opções, por isso a moda das idades é 16.

Para encontrar a mediana, como são sete idades e esse é um número ímpar, não precisa fazer conta, basta escolher o termo central da lista. Você achou 18 de mediana? 👀

Eita! Se a resposta é sim, você caiu no bait da mediana! O maior erro nos exercícios de mediana é esquecer de organizar a lista em ordem crescente. Assim, a lista ficaria dessa forma:

16 16 16 17 17 18 19

Como o termo central da lista de idades, depois de organizar em ordem crescente, foi 17, a mediana das idades é 17. Percebeu como cada uma das medidas de tendência central tem um processo diferente para encontrar seu valor? Por isso, tenha atenção ao resolver as questões!

3. Geometria espacial

Vamos ao terceiro dos assuntos de Matemática que mais caem no Enem? Na geometria espacial, os conteúdos que você precisa saber para se dar bem na prova estão relacionados à geometria de posição, prismas e cilindros. Há outros que estão fora do nosso foco, como pirâmides, esferas e poliedros, que são potencialmente mais complexos, mas, fazer o que? Prioridades! 🙃

Geometria de posição

Chamamos de geometria de posição os tópicos relacionados à projeção e análise de posições possíveis entre retas e planos. Temos dois exemplos nas imagens abaixo:

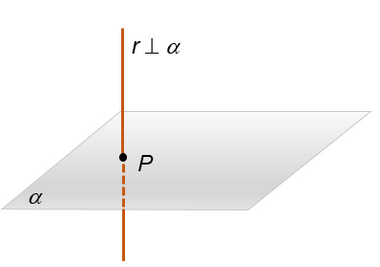
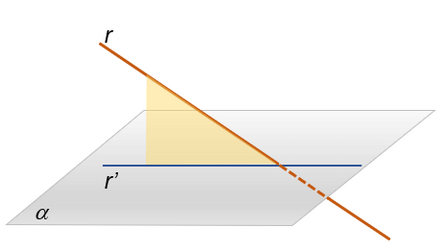
Volumes e áreas

Em relação aos prismas e cilindros, o foco costuma ser nos cálculos de superfícies e volumes de sólidos. Para calcular a área da superfície de um sólido, você precisa somar as duas bases, superior e inferior, e a área lateral (A_L).

Por outro lado, para calcular o volume de prismas e cilindros, você só precisa multiplicar a área da base (A_B) pela altura (h). A ilustração a seguir traz três exemplos:

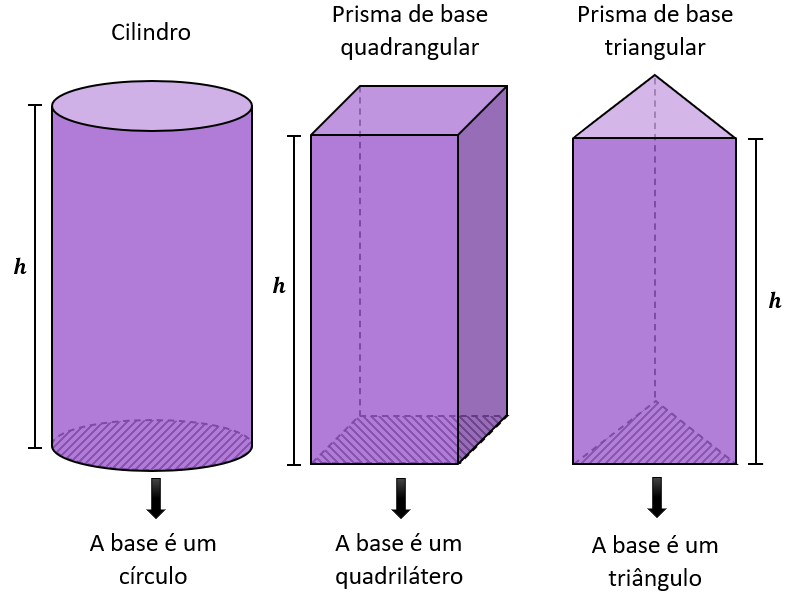
• Volume de prismas e cilindros: \(V = A_B \cdot h\)
• Área total de prismas e cilindros: \(A_T = 2 ⋅ A_B + A_L\)

🚨 Fique atento: em algumas questões do Enem, o volume está associado à capacidade interna de um sólido, capacidade em metros cúbicos (m³) ou litros🚨

Exercício de geometria espacial

(Enem) Alguns objetos, durante a sua fabricação, necessitam passar por um processo de resfriamento. Para que isso ocorra, uma fábrica utiliza um tanque de resfriamento, como mostrado na figura.

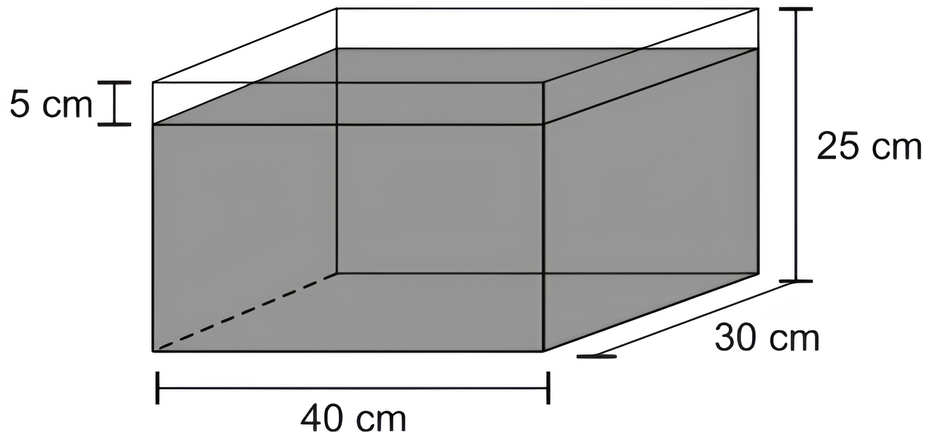
O que aconteceria com o nível da água se colocássemos no tanque um objeto cujo volume fosse de 2.400 \(\text{cm}^{3}\)

a) O nível subiria 0,2 cm, fazendo a água ficar com 20,2 cm de altura.   

b) O nível subiria 1 cm, fazendo a água ficar com 21 cm de altura.   

c) O nível subiria 2 cm, fazendo a água ficar com 22 cm de altura.   

d) O nível subiria 8 cm, fazendo a água transbordar.   

e) O nível subiria 20 cm, fazendo a água transbordar.

Resposta: [C]
O primeiro passo é calcular o volume atual do tanque, para isto basta apenas multiplicar os valores das três dimensões atuais, assim temos:

\(40\times 30\times \left(25-5\right)=40\times 30 \times 20=24000\;\text{cm}^3\)

Sabendo que atualmente temos \(24000\;\text{cm}^3\) iremos adicionar \(2400\;\text{cm}^3\), assim \(24.000 + 2400=26400\;\text{cm}^3\)

Com a adição deste objeto, sabemos que o nível da água irá aumentar, assim chamaremos desta medida de h. Logo \(40\times 30 \times h = 26400\;\text{cm}^3\)

\(1200\times h=26400\;\text{cm}^3\) 

\(h=\dfrac{26400}{1200}=22\) cm

Dessa forma, a nova altura da água é 22 cm, como anteriormente ela estava com 20 cm, obteve um aumento de 2 cm.

4. Geometria plana

Um conteúdo mais do que especial em Matemática no Enem é o de geometria plana, pois, além de ter uma incidência alta, vai salvar sua pele em geometria espacial. Os assuntos mais frequentes são polígonos regulares, circunferência e círculo, áreas de figuras planas e perímetro.

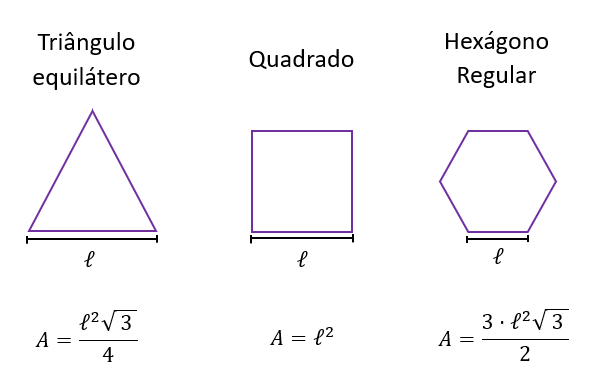
Polígonos regulares

Entre os polígonos regulares, os que mais caem no Enem são os triângulos equilátero, quadrado e hexágono. Eles têm todos os ângulos e lados com a mesma medida, por isso, para calcular suas áreas basta ter o valor de um de seus lados. Veja as ilustrações de cada um com suas respectivas fórmulas:

Circunferência e círculo

Sobre circunferência e círculo, encontramos os tópicos: comprimento da circunferência, área do círculo, área do setor, área do segmento circular e área da coroa circular. Bastante, né? Mas vamos dar atenção para o básico, que é bater o olho em um círculo de raio r e conseguir calcular área e comprimento da sua circunferência.

O perímetro é a soma dos lados de um polígono. Como polígonos podem ter muitos lados, o perímetro varia de acordo com cada caso, então é preciso ter atenção com questões que envolvam esse tópico.

Lembrando que a circunferência nada mais é que o 'perímetro' do círculo. Em um círculo de raio r, o comprimento da circunferência é dada por \(C = 2 \pi r\).

Fórmulas de áreas recorrentes

Um dos carros-chefes da geometria plana é o conteúdo de áreas, então encerramos este top 4 reforçando sua importância e formalizando esse conceito.

Podemos entender a área como a medida bidimensional de uma superfície, em que temos conhecimento do comprimento e largura. Para além dos polígonos já apresentados, veja abaixo três polígonos que precisam fazer parte do seu repertório no Enem e suas fórmulas:

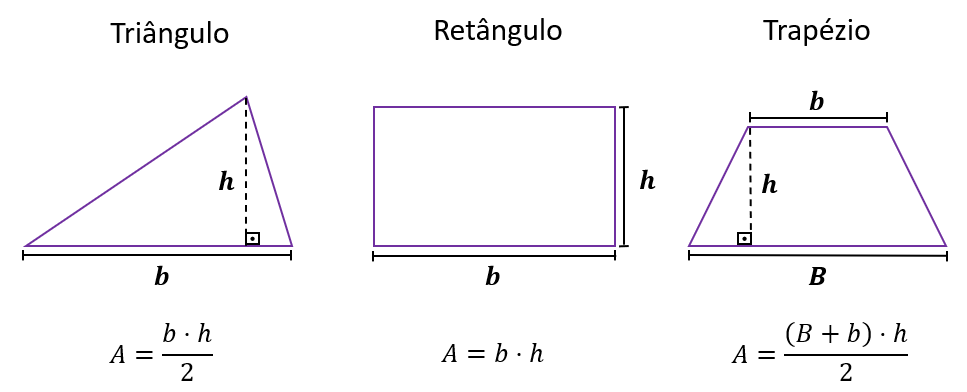
🔔 Algumas figuras geométricas não têm fórmulas diretas para o cálculo da sua área, mas é possível dividir a figura em partes menores que você saiba calcular a área 🔔

5. Funções

As definições de função que tratam do domínio, contradomínio e imagem, do ponto de vista de conjuntos, são importantes para entender o conteúdo, mas dificilmente cobradas em Matemática no Enem.

Tópicos de paridade de funções, injetividade, sobrejetividade, função inversa e composições também são raros e não merecem tanta atenção.

Mas se tudo isso não é recorrente, então qual a parte de funções que cai no Enem? Funções do primeiro e segundo grau, análise de crescimento e decrescimento de funções, inequações e análise de máximos e mínimos são os assuntos que mais aparecem.

Função do primeiro grau

Uma das funções mais versáteis é a função do primeiro grau. Além de aparecer em Matemática no Enem, ela adora aparecer nas questões de Física. É, portanto, uma função multidisciplinar. A forma algébrica dessa função é a seguinte:

\(f(x) = ax + b, \;\text{com} \;a, \;b \in \mathbb{R} \;\text{e} \;a \neq 0\)

Esses coeficientes 𝑎 e 𝑏 dão informações que podem ser a chave da resolução da questão! Então, você precisa saber interpretá-los e lembrar algumas coisas.

• O coeficiente 𝑎 também é chamado de coeficiente angular da reta. É ele que indica se o comportamento da reta é crescente ou decrescente;

  - \(a > 0\), reta crescente. 
  - \(a < 0\), reta decrescente. 

• O coeficiente 𝑏 é chamado de coeficiente linear da reta. Ele indica o ponto em que o gráfico corta o eixo y;
  
• A raiz ou zero da função do primeiro grau é o valor de x que faz com que o valor de y seja zero. Graficamente, é onde a reta toca o eixo x;

Função do segundo grau

A função do segundo grau divide opiniões toda vez que é necessário encontrar as raízes dela - há quem goste de usar a fórmula de Bhaskara e quem prefere usar soma e produto. Na verdade, o importante é você se garantir na resolução, pois ambos os métodos chegam no mesmo resultado.

A forma algébrica dessa função é

\(f(x) = ax^2 + bx + c, \;\text{com} \;a,\; b,\; c \in \mathbb{R} \;\text{e}\; a \neq 0\)

Assim como na função de primeiro grau, você precisa saber interpretar. Mas, neste caso, temos três coeficientes 𝑎, 𝑏 e c. Na função de segundo grau, é importante lembrar que:

• O coeficiente 𝑎 determina a concavidade da parábola

  - \(a > 0\), concavidade para cima. 
  - \(a < 0\), concavidade para baixo. 

• O coeficiente c indica o ponto em que o gráfico corta o eixo y;
  
• As raízes ou zeros da função do segundo grau, onde a parábola toca o eixo x, podem ser encontradas a partir de

  Fórmula de Bhaskara

\(x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\)

 Soma e produto

• O ponto de máximo ou mínimo é o vértice da parábola e pode ser encontrado com as fórmulas

Nomenclaturas e padrões gráficos

Uma última dica sobre funções é que nem sempre a questão deixa explícito o tipo de função requisitada. Veja algumas palavras que ajudam a identificar funções e elementos visuais dos gráficos para otimizar seu tempo de prova:

• Linear, proporcional e função afim, em geral, são palavras relacionadas às funções de primeiro grau: \(\color{black}{f(x) = ax + b}\)
  
• Parábola e funções quadráticas se referem às funções de segundo grau: \(\color{black}{f(x) = ax^2+ bx + c}\)
  
• Gráficos com períodos que se repetem, em geral, são relacionados às funções trigonométricas.
  
• Gráficos de retas, em geral são associados às funções do primeiro grau ou funções constantes.

Exercício de função

(Enem) Em jogos de voleibol, um saque é invalidado se a bola atingir o teto do ginásio onde ocorre o jogo. Um jogador de uma equipe tem um saque que atinge uma grande altura. Seu recorde foi quando a batida do saque se iniciou a uma altura de 1,5 m do piso da quadra, e a trajetória da bola foi descrita pela parábola \(y=-\dfrac{x^2}{6}-\dfrac{7x}{3}+12\), em que \(y\) representa a altura da bola em relação ao eixo \(x\) (das abscissas) que está localizado a 1,5 m do piso da quadra, como representado na figura. Suponha que em todas as partidas algum saque desse jogador atinja a mesma altura do seu recorde.

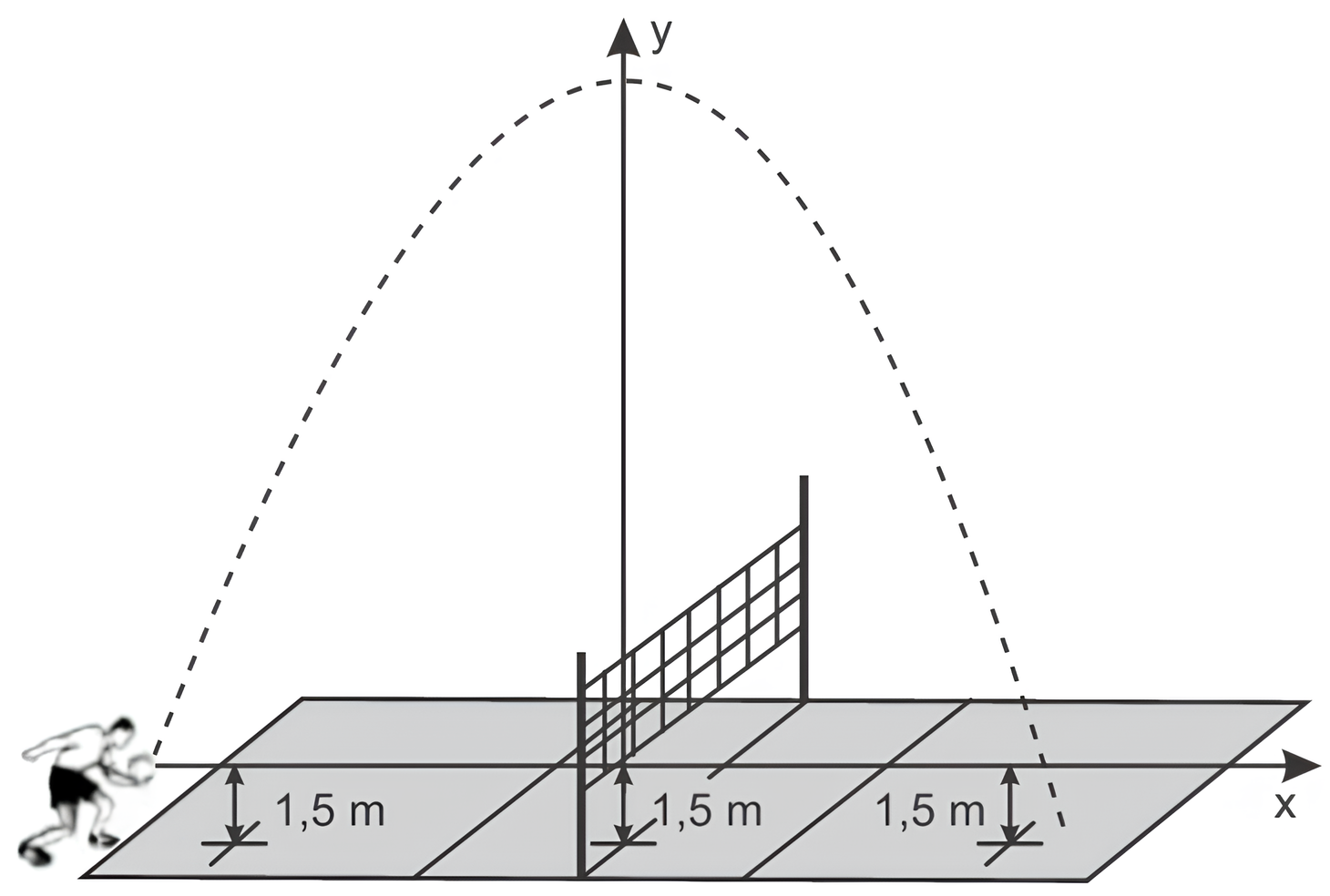
A equipe desse jogador participou de um torneio de voleibol no qual jogou cinco partidas, cada uma delas em um ginásio diferente. As alturas dos tetos desses ginásios, em relação aos pisos das quadras, são:

• ginásio l: 17 m;
• ginásio II: 18 m;
• ginásio III: 19 m;
• ginásio IV: 21 m;
• ginásio V: 40 m.

O saque desse atleta foi invalidado

a) apenas no ginásio I.

b) apenas nos ginásios I e II.

c) apenas nos ginásios I, II e III.

d) apenas nos ginásios I, II, III e IV.

e) em todos os ginásios.  

Resposta: [D]
Esta é uma questão em que nos interessa a maior altura de um saque que é descrito por uma função do 2º grau, então nossa estratégia será calcular o \(y\) do vértice  \(y_v\)dessa parábola, já que essa será a altura máxima atingida pela bola. Primeiramente, vamos identificar na função os coeficientes:

\(y=-\dfrac{x^2}{6}-\dfrac{7x}{3}+12\) em que

\(a=-\dfrac{1}{6}\;b=-\dfrac{7}{3}\;c=12\)

O nosso valor de interesse pode ser calculado através da fórmula:

\(y_v=-\dfrac{\Delta}{4a}\) em que \(\Delta=b^2-4ac\)

\(y_v=-\dfrac{\left(-\dfrac{7}{3}\right)^2-4\cdot \left(-\dfrac{1}{6}\right)\cdot 12}{4\cdot \left(-\dfrac{1}{6}\right)}=\dfrac{\frac{49}{9}+\frac{48}{6}}{-\frac{4}{6}}=-\dfrac{\frac{49}{9}+8}{-\frac{2}{3}}=-\dfrac{\frac{49+72}{9}}{-\frac{2}{3}}\)

\(=-\dfrac{\frac{121}{9}}{-\frac{2}{3}}=-\left(\dfrac{121}{9}\cdot \left(-\dfrac{3}{2}\right)\right)=-\left(-\dfrac{121}{6}\right)=\dfrac{121}{6}\)

A maior altura alcançada pelo saque é \(\dfrac{121}{6}\), mas esse saque está sendo dado a 1,5 metros do piso da quadra. Como as alturas dos ginásios são dadas em relação ao piso, precisamos somar 1,5 à altura alcançada no saque para decidir em quais ginásios o saque foi invalidado. Vamos transformar a fração em decimal arredondando em uma casa decimal:

\(\dfrac{121}{6}\cong 20,1\)

Agora basta somar este valor com a altura em relação ao chão:

\(20,1+1,5=21,6\)

Dessa forma, o saque do jogador em questão atingiu aproximadamente 21,6 m. Como os ginásios I, II, III e IV têm alturas menores que 21,6 m em todos estes, pelo menos um saque foi invalidado. Apenas no ginásio V este jogador pode sacar seu saque com altura máxima.

Agora que você já sabe quais assuntos de Matemática mais caem no Enem, seus estudos para o exame em 2024 vão render muito mais!

🥇 Quer preparação máxima para ter alto rendimento no Enem e vestibulares e ingressar no curso dos seus sonhos? Então vem com a gente!