Dicas fundamentais para interpretar gráficos e tabelas
Explore exemplos para aprimorar suas habilidades e conquistar mais confiança ao resolver as questões de Matemática
Acessibilidade
Dominar a interpretação de gráficos e tabelas é essencial em um mundo repleto de informações visuais. À medida que a quantidade de dados disponíveis continua a crescer, a habilidade de extrair informações significativas dessas representações visuais torna-se cada vez mais valiosa.
Os gráficos traduzem com mais precisão um conjunto de dados. Com eles, podemos, em segundos, entender dimensão, quantidade e evolução das variáveis que estamos estudando e decidir como usá-las.
NAVEGUE PELOS CONTEÚDOS
Gráficos e interpretação de problemas
Antes de mergulhar no universo dos gráficos e tabelas, seus elementos, tipos e dicas, trouxemos um exemplo de como tudo isso é importante para a interpretação de problemas.
Considere uma loja que vende três produtos A, B e C. O dono da loja decide analisar o histórico de vendas de 2022 para saber em qual mês que ele obteve o maior número de vendas. Consultando sua base de dados ele se depara com a seguinte tabela:
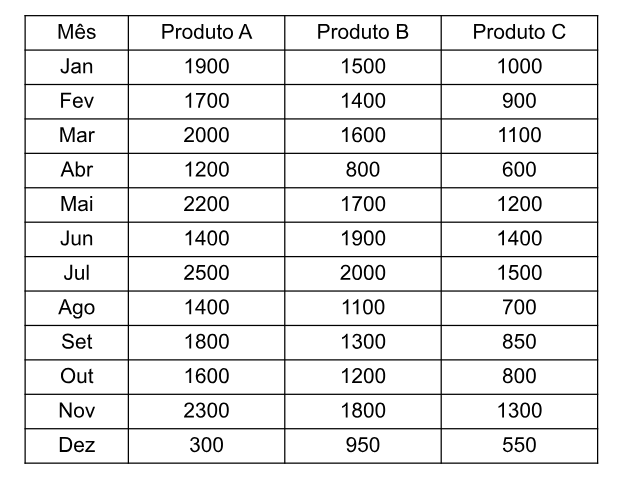
Uma possível solução para encontrar o mês que obteve o maior número de vendas é somar o que foi vendido de cada produto mensalmente e, então, comparar mês a mês.

Mas isso é muito trabalhoso, não acha?
Além de ser cansativo, no caso de conjuntos de dados maiores e usando esse método, poderíamos levar anos para encontrar a resposta que desejamos.
A solução é transformar esses dados em um gráfico de colunas, no qual a altura da coluna representa o volume de vendas. Meses que obtiveram um volume de vendas maior consequentemente terão um altura maior, conforme o gráfico a seguir:
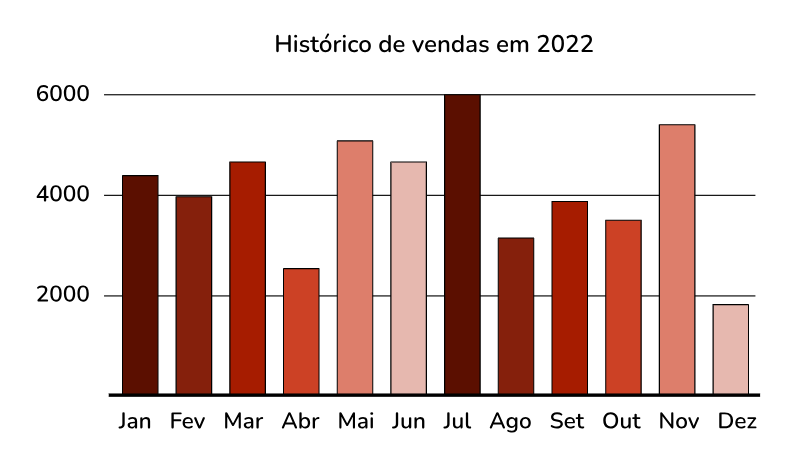
Por meio da representação gráfica, ficou mais simples observar que o mês de julho se destacou ao registrar o mais significativo volume de vendas.
Agora que você já viu como usar gráficos é útil e pode facilitar a resolução de problemas, vamos conhecer mais sobre eles?
Quais os elementos de um gráfico?
Quando estamos construindo um gráfico, é fundamental considerar certos elementos essenciais para a sua compreensão. A disposição das informações no gráfico precisa estar nítida, pois isso garante que os resultados finais mostrem a essência da pesquisa realizada, alinhando-se com seu propósito original.
Aqui estão os principais elementos de um gráfico:
- título
Um título claro e conciso que descreve o conteúdo do gráfico e o que está sendo apresentado.
- eixos
Os eixos \(x\) e \(y\) (horizontal e vertical) são linhas que fornecem orientação e dimensionamento para os dados. O eixo \(x\) normalmente representa a variável independente, enquanto o eixo \(y\) representa a variável dependente.
- rótulos dos eixos
Os rótulos nos eixos \(x\) e \(y\) descrevem as unidades ou categorias dos dados sendo plotados. Eles ajudam a entender o contexto dos valores apresentados.
- legenda
A legenda identifica as diferentes séries de dados ou categorias representadas no gráfico, o que é especialmente importante na interpretação de gráficos com várias linhas, barras ou pontos.
- série de dados
Uma série de dados é um conjunto de valores relacionados que serão plotados no gráfico. Cada série de dados tem cor ou símbolo único.
- marcadores de dados
Pontos, barras, linhas ou outros símbolos que representam os valores específicos de cada ponto de dados no gráfico.
Lembre-se: nem todos os tipos de gráficos contemplam esses elementos, por isso é importante se atentar ao contexto dos dados.
6 principais tipos de gráficos
Diferente tipos de gráficos exigem diferentes elementos. Portanto, é necessário conhecer quais são eles e as suas particularidades.
Listamos os seis tipos de gráficos mais comuns em questões de Matemática do Enem e outros vestibulares:
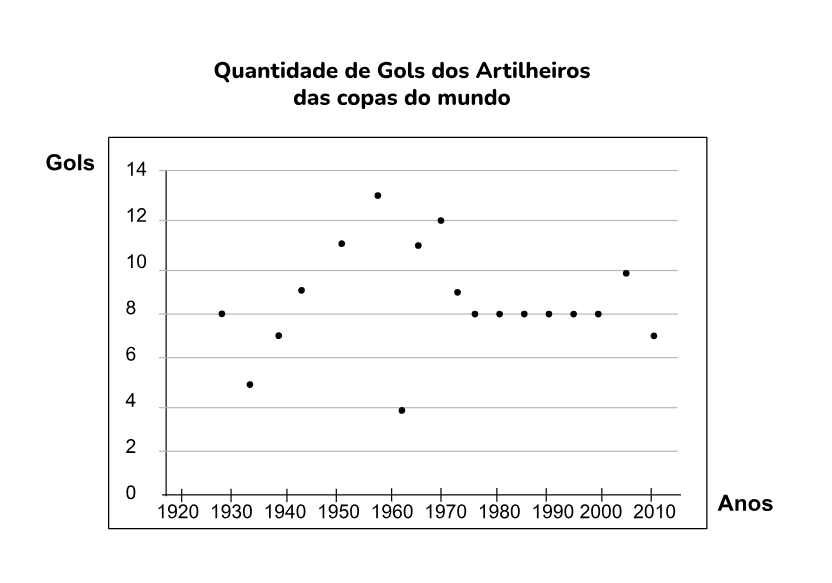
1. Gráfico de pontos
O gráfico de pontos, também conhecido como scatter plot, é uma representação visual que exibe os valores de duas variáveis para cada ponto de dados em um plano cartesiano. Ele é amplamente utilizado para explorar a relação entre duas variáveis, identificar padrões de dispersão e possíveis correlações.
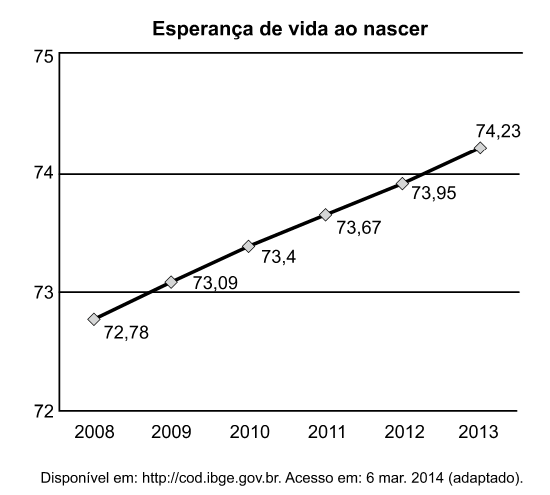
2. Gráfico de linha
O gráfico de linha é uma representação visual que traça pontos de dados conectados por linhas retas. Normalmente, o utilizamos para exibir tendências, variações e mudanças ao longo do tempo ou em uma sequência ordenada. É uma ferramenta poderosa para visualizar dados contínuos e entender padrões.
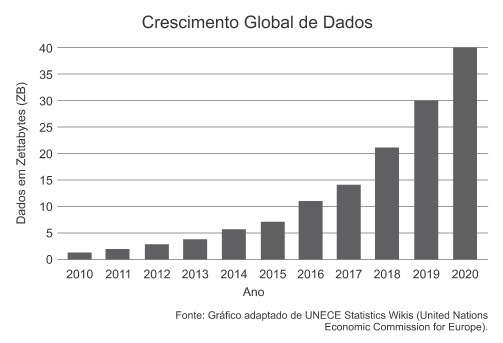
3. Gráfico de colunas
O gráfico de colunas é um dos mais comuns e eficazes na representação visual de dados, frequentemente usado para comparar valores entre diferentes categorias. Serve a diversos campos, como negócios, ciências sociais, economia e outros.
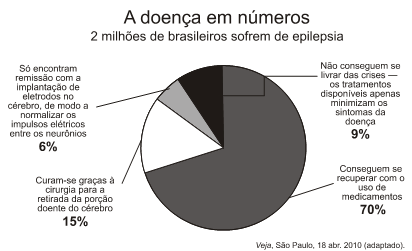
4. Gráfico de setor ou de pizza
O gráfico de setores, também conhecido como gráfico de pizza 🍕, é uma forma popular de visualizar a distribuição proporcional de diferentes partes em um todo. Esse tipo de gráfico é frequentemente na representação de categorias ou porcentagens em relação a um total.
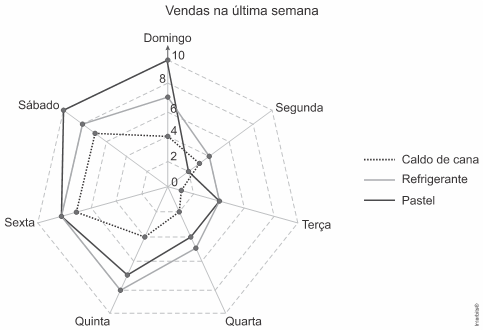
5. Gráfico em rede ou de grafo
O gráfico em rede, ou gráfico de grafo, é uma representação visual que mostra as relações entre diferentes elementos. Podemos utilizá-lo para ilustrar conexões, interações e fluxos em uma rede complexa.
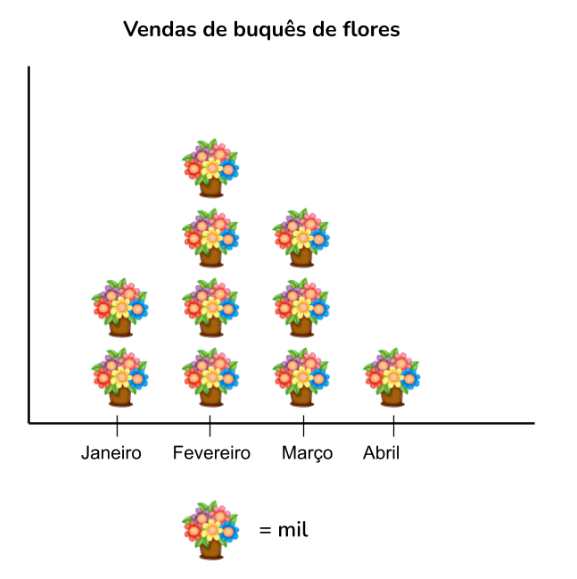
6. Gráfico pictórico, de imagens ou icônico
O gráfico pictórico, gráfico de imagens ou gráfico icônico, utiliza ícones ou imagens para transmitir informações quantitativas de maneira mais intuitiva e envolvente. Em vez de usar barras, linhas ou pontos, o gráfico pictórico utiliza símbolos visuais para representar dados.
Dicas para fazer uma boa interpretação de gráficos
Interpretar gráficos de maneira eficaz é essencial para compreender e comunicar as informações que estão neles. Observe o tipo de gráfico e as unidades indicadas, para entender claramente as referências dos eixos horizontais e verticais.
Se o gráfico não se encaixa no plano cartesiano tradicional, preste atenção especial às unidades de cada variável e às suas características específicas.

Reunimos dicas pontuais para
ajudar na interpretação de gráficos:
- observe a escala
Verifique se os eixos têm escalas lineares ou logarítmicas e confira as unidades. A escala pode influenciar o modo como as diferenças são percebidas.
- identifique as séries de dados
Se o gráfico tiver múltiplas séries de dados, use a legenda para identificar cada uma. As cores e os padrões podem ajudar a diferenciá-las.
- análise de tendências
Observe padrões de subida, descida, variação ou estabilidade ao longo do gráfico. Identifique tendências, como crescimento, declínio ou flutuações.
- pontos em destaque
Identifique pontos notáveis, como picos, vales ou pontos de transição. Eles podem indicar eventos significativos ou momentos de mudança.
- considerações de escala
esteja ciente de como a escala dos eixos pode influenciar a percepção dos dados. Uma escala enganosa tende a distorcer a interpretação.
E aí, anotou essas dicas? Não se esqueça de que interpretar gráficos exige atenção aos detalhes, compreensão das variáveis em jogo e consideração do contexto. Quanto mais prática você tiver, melhor será em obter informações significativas dos gráficos que analisar.
Dica extra: como fazer a interpretação de tabelas
A tabela estatística é uma representação organizada de dados, que, assim como os gráficos, visa resumir, comparar e analisar informações de maneira eficiente. Veja:
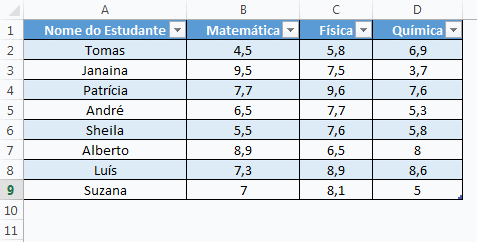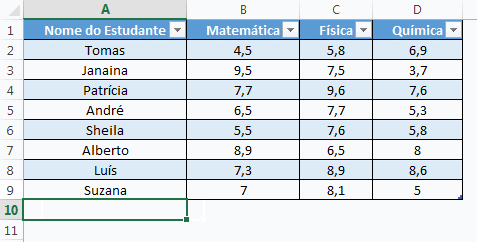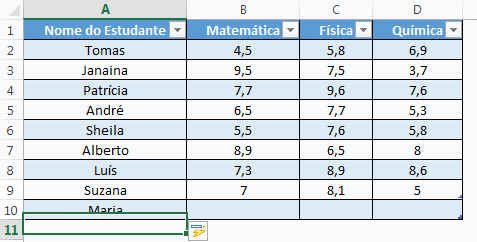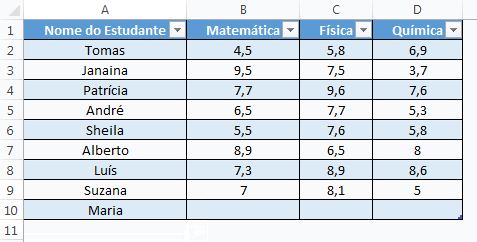
Interpretar tabelas de forma eficaz envolve, inicialmente, a leitura do título e cabeçalhos para compreender o contexto e as variáveis apresentadas. Analisar padrões, totais, subtotais e comparar valores é crucial para identificar tendências e relações nos dados.
Dê atenção especial às notas de rodapé, porcentagens e proporções, pois isso ajuda a compreender detalhes importantes. A contextualização dos dados, a transformação em gráficos e a formulação de perguntas analíticas auxiliam na interpretação.
Além disso, relacionar os dados ao seu conhecimento prévio pode fornecer ideias mais profundas, tornando a interpretação de tabelas uma habilidade cada vez mais refinada com a prática contínua.
Problema com interpretação de tabelas
Veja um exemplo de exercício que já apareceu no Enem (2012):
Uma pesquisa realizada por estudantes da Faculdade de Estatística mostra, em horas por dia, como os jovens entre 12 e 18 anos gastam seu tempo, tanto durante a semana (de segunda-feira a sexta-feira), como no fim de semana (sábado e domingo). A seguinte tabela ilustra os resultados da pesquisa.
| Rotina juvenil | Durante a semana | No fim de semana |
|---|---|---|
| Assistir à televisão | 3 | 3 |
| Atividades domésticas | 1 | 1 |
| Atividades escolares | 5 | 1 |
| Atividades de lazer | 2 | 4 |
| Descanso, higiene e alimentação | 10 | 12 |
| Outras atividades | 3 | 3 |
De acordo com esta pesquisa, quantas horas de seu tempo gasta um jovem entre 12 e 18 anos, na semana inteira (de segunda-feira a domingo), nas atividades escolares?
a) 20
b) 21
c) 24
d) 25
e) 27
Resposta [E]
O termo "Durante a semana" representa os 5 dias úteis (segunda, terça, quarta, quinta e sexta). Com base na interpretação da tabela, a linha com "Atividades escolares" segue os valores referentes à categoria, assim, durante a semana os alunos gastam, em média, 5 horas por dia em atividades escolares e 1 uma por dia aos finais de semana (sábado e domingo).
Durante toda a semana, eles gastam 5 horas em 5 dias, então 5 · 5 = 25.
Durante todo o final de semana, eles gastam 1 hora em 2 dias, então 1 · 2 = 2
25 + 2 = 27 horas de seu tempo, durante a semana inteira, com atividades escolares.
Exemplos e exercícios com gráficos resolvidos
Confira alguns exercícios de interpretação de gráficos resolvidos:
Exemplo 1
(Enem digital) O gráfico mostra as receitas e as despesas de uma empresa nos meses de julho a novembro de um ano. O resultado financeiro, obtido pela diferença entre receita e despesa, pode ser positivo (lucro) ou negativo (prejuízo).
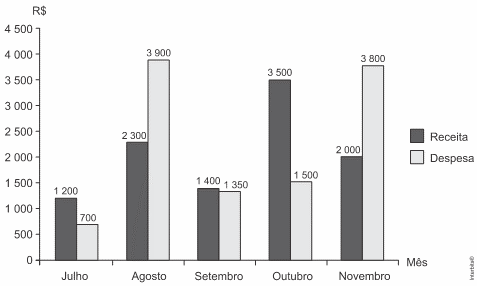
Sabendo que o mês de dezembro é, em geral, de melhores vendas, o dono da empresa faz uma previsão de que a receita naquele mês terá um aumento, em relação ao mês anterior, com a mesma taxa de crescimento ocorrida de setembro para outubro, e que a despesa irá se manter a mesma de novembro.
Se confirmadas as previsões do dono da empresa, o resultado financeiro a ser obtido no semestre de julho a dezembro será um
a) prejuízo de R$ 2.650,00.
b) prejuízo de R$ 850,00.
c) lucro de R$ 7.150,00.
d) lucro de R$ 5.950,00.
e) lucro de R$ 350,00.
Resposta [E]
Temos que a taxa de crescimento na receita de setembro para outubro foi de: (3500 - 1400)/(1400) = 1,5
A receita de novembro foi de: 2000, logo a receita esperada para o mês de dezembro é de:
(1 + 1,5) · 2000 = 5000 reais
Agora calculando a diferença de receitas de cada mês, temos que:
Julho: 1200 - 700 = 500 (lucro)
Agosto: 2300 - 3900 = - 1600 (prejuízo)
Setembro: 1400 - 1350 = 50 (lucro)
Outubro: 3500 - 2000 = 2000 (lucro)
Novembro: 2000 - 3800 = -1800 (prejuízo)
Dezembro: 5000 - 3800 = 1200 (lucro)
Somando tudo temos que a resposta pedida foi: 500 - 1600 + 50 + 2000 - 1800 + 1200 = R$ 350,00 (lucro)
Exemplo 2
(Enem) O termo agronegócio não se refere apenas à agricultura e à pecuária, pois as atividades ligadas a essa produção incluem fornecedores de equipamentos, serviços para a zona rural, industrialização e comercialização dos produtos.
O gráfico seguinte mostra a participação percentual do agronegócio no PIB brasileiro:
Esse gráfico foi usado em uma palestra na qual o orador ressaltou uma queda da participação do agronegócio no PIB brasileiro e a posterior recuperação dessa participação, em termos percentuais.
Segundo o gráfico, o período de queda ocorreu entre os anos de
a) 1998 e 2001.
b) 2001 e 2003.
c) 2003 e 2006.
d) 2003 e 2007.
e) 2003 e 2008.
Resposta [C]
Denotando os momentos de subidas pelas cor verde e os momentos de descida pela cor vermelha, fazendo a interpretação do gráfico, temos a seguinte configuração:
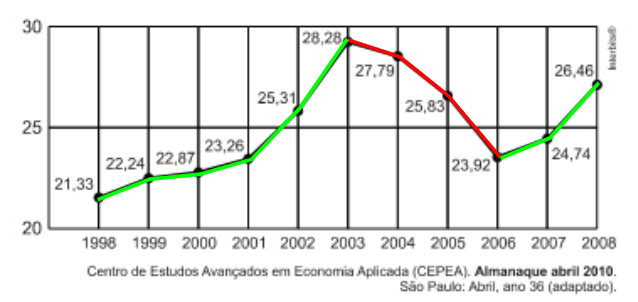
O período de queda, portanto, foi entre 2003 e 2006
👉 Leia também:
Vença o medo da Matemática com essas dicas de estudo
Números inteiros: o que são eles e como aparecem na Matemática?