Início » Função do primeiro grau: veja o guia completo para resolver questões

Função do primeiro grau: veja o guia completo para resolver questões

Entenda o que são funções do primeiro grau, como classificá-las e de que forma identificar seus coeficientes e tipos para arrasar no Enem e grandes vestibulares

18/01/2024

Mulher escrevendo fórmulas de função do primeiro grau em lousa verde com giz

Acessibilidade

Função do primeiro grau, função afim ou função linear. Tantos nomes para tratar de um mesmo assunto, não é mesmo? Parece confuso, mas eu garanto que a partir de hoje, você vai entender tudo sobre esse tipo de função tão importante na jornada de estudos.

A gente vai saber qual o comportamento da função de primeiro grau, todas as formas em que ela se apresenta, como encontrá-la, sua representação gráfica e ainda, dicas infalíveis para...

Personagem Howard Wollowitz, de The Big Bang Theory fazendo uma trocadilho com a função afim e estar afim de alguém

... você se tornar um mestre no assunto!

NAVEGUE PELOS CONTEÚDOS

Definição de função do primeiro grau

Podemos entender a função como uma relação de dependência entre duas grandezas. Neste caso, uma função real do primeiro grau é definida por $f: \mathbb{R} \rightarrow \mathbb{R}$ onde $f(x) = a \cdot x + b$ e representada graficamente por uma reta. Agora, você deve estar se perguntando: "O que é esse monte de letras?". Então, vamos por partes!

$x$ é nossa variável, ela determinará o valor de $f$ para cada número que $x$ assumir;
$a$ é chamado de coeficiente angular, que define quão inclinada será nossa função;
$b$ é o coeficiente linear, que define onde a função corta o eixo $y$.

Durante nosso texto, você irá entender de forma geométrica quais são os papéis de $a$ e $b$.

Outros nomes da função do primeiro grau

Como explicamos lá no início, a função do primeiro grau também tem outros nomes. São eles:

Função afim: existem várias linhas de pensamento que tentam explicar esse nome, mas o termo "afim" vem do grego affīnis, que significa ter afinidade, semelhança ou ligação. Acredita-se que sua origem vem do fato de dois pontos definirem uma única reta, ou seja, estarem ligados. Mais ainda, o $a$ é diferente de 0;
Função linear: esse é apenas um caso particular da função do primeiro grau, onde $b = 0$;
Função constante: outro caso particular, onde $a = 0$. Ou seja, $f(x) = b$.

Coeficientes

Até agora, falamos muito sobre $a$ e $b$, porém ainda não explicamos os seus significados. Por isso, vamos mostrar na prática como eles se comportam geometricamente.

Coeficiente angular

O $a$ é chamado de coeficiente angular, pois está diretamente relacionado ao ângulo que o gráfico forma com o eixo $x$. $a$ é um número real ($\mathbb{R}$). Então, temos três opções de valores para ele:

$a > 0$;
$a = 0$;
$a < 0$.

Para cada uma dessa opções, há três representações gráficas, e o gráfico de uma função do primeiro grau é uma reta. Dessa maneira, teremos os três possíveis casos ilustrados a seguir:

Três planos cartesianos exemplificando o coeficiente angular da função do primeiro grau. O primeiro é a maior que zero, em que a reta atravessa o zero no eixo x e y. O segundo gráfico é uma reta horizontal cruzando o número um positivo no eixo y, representando a igual a zero. O terceiro gráfico representa a menor do que zero. A reta corta os pontos um positivo no eixo y e um positivo no eixo x

Coeficiente linear

O $b$ é o coeficiente linear ou termo independente. Ele é independente porque não é multiplicado por $x$ (na verdade, é, mas se trata de um $x^{0} = 1$. No entanto, não vamos nos prender a esse detalhe 🤫). Outra característica muito importante do coeficiente linear é informar onde a reta corta o eixo $y$. Ele também é um número real ($\mathbb{R}$) e tem três possíveis valores:

$b > 0$;
$b = 0$;
$b < 0$.

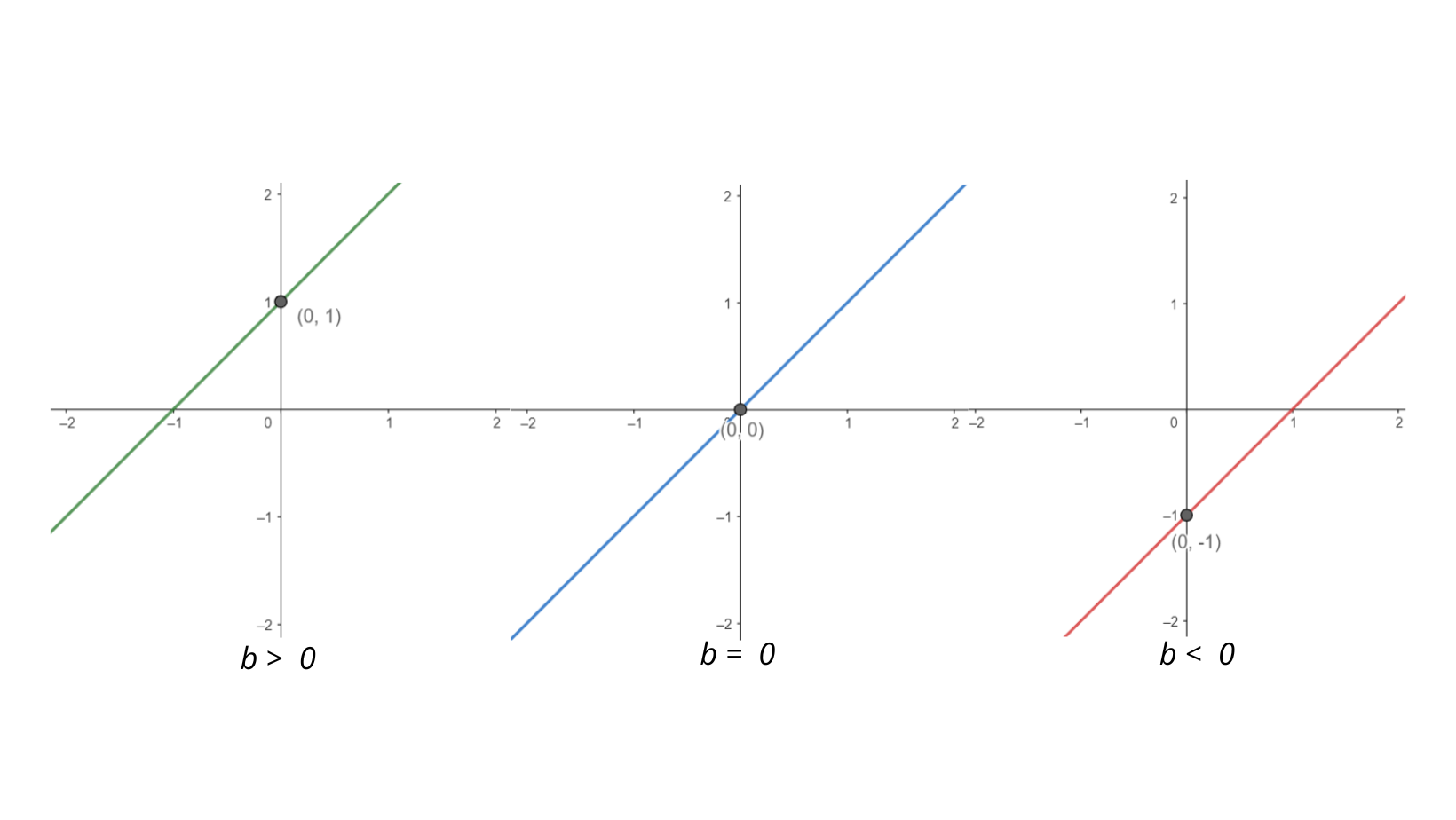
Três gráficos representando o coeficiente linear na função do primeiro grau. O primeiro gráfico representa b maior do que zero, marcando ponto zero um no eixo y. O segundo gráfico mostra b igual a zero, identificando o ponto zero zero no eixo y. O terceiro gráfico mostra b menor do que zero, mostrando o ponto zero um negativo no eixo y.

Como nosso gráfico está no plano ℝ², os pontos que pertencem à reta são da forma (x, y) = (x, ax + b). Assim, quando x = 0, temos o ponto (0, b), como você pode observar nos gráficos acima.

Dicas fundamentais para interpretar gráficos e tabelas

Regra de três: simples, composta, como calcular e exercícios

Função crescente x função decrescente: entenda a diferença

Você deve ter reparado que, dependendo do valor do a, o gráfico tem um comportamento diferente. Isso se dá em função da taxa de crescimento da função. Vamos, então, definir o que são funções crescentes e decrescentes e apresentar a principal diferença entre elas.

Função crescente

Dizemos que $f: \mathbb{R} \rightarrow \mathbb{R}$ é crescente se, para cada $x_0, x_1 \in \mathbb{R}$ tal que $x_0 < x_1$, temos que $f(x_0) < f(x_1)$.

Parece ser algo de outro mundo não é mesmo? Mas é mais fácil do que você imagina!

Para as funções afim, precisamos avaliar o sinal do $a$. Então, quando uma função afim for crescente, o $a > 0$. Basicamente, o que essa definição diz é: se pegarmos dois números em nosso eixo $x$, onde o primeiro é menor que o segundo, o valor de $f(x)$ (ou seja, o valor em $y$) do primeiro será menor que o segundo.

Observe que aqui estamos falando em maior e menor, no sentido literal e não em questão de tamanhos ou distâncias.

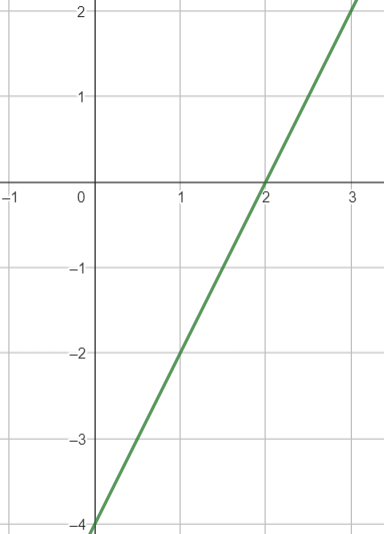
Gráfico de plano cartesiano mostrando uma função crescente. A reta atravessa quatro negativo no eixo y e dois positivo no eixo x — Função crescente.

No gráfico acima, considerando os valores de $x = 0$ e $x_1 = 2$, temos que $f(x_0) = -4$ e $f(x_1) = 2$. Em questões de tamanho, ou seja, distância até a origem, $-4$ é "maior" que $2$, pois $|-4| = 4 >2$. Mas isso não será importante nesse momento para nós, pois queremos olhar para o valor de cada um com seus respectivos sinais. Sendo assim, $-4 < 2$ como já estamos acostumados.

Funções decrescentes

Uma função é dita decrescente quando para $x_0 < x_1 $ reais, temos que $f(x_0) > f(x_1)$

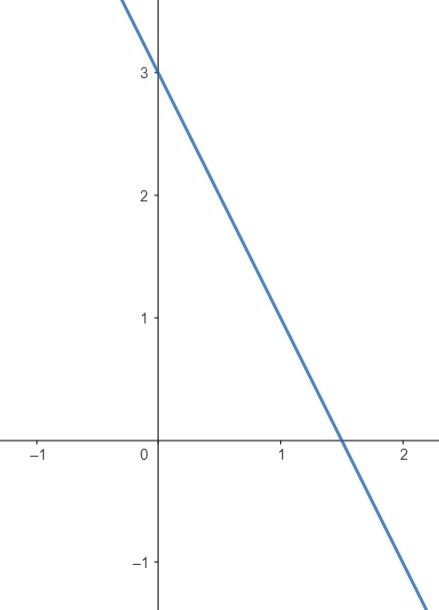
De forma análoga ao que fizemos com a função crescente, temos a mesma ideia para funções decrescentes. Agora, quanto maior forem os $x$'s, menores serão suas imagens. Também, ao tratarmos das funções do primeiro grau, temos que $a < 0$.

Exemplo de função decrescente do primeiro grau mostrando reta cruzando o eixo y no ponto três positivo e o eixo x no ponto um e meio positivo — Função decrescente.

Raiz (zero) da função: o que é e como calcular

Para encerrar com chave de ouro, vamos falar sobre o que são e como calcular as raízes de uma função.

Plano cartesiano mostrando reta cruzando o ponto dois vírgula zero no eixo x

A raiz de uma função, de forma geral, é o valor de $x$ no qual a função $f(x) = 0$ e a notação de pontos do espaço para as raízes será $(x, 0)$, como no exemplo acima. No caso das funções do primeiro grau, teremos a seguinte expressão:

\[ a \cdot x + b = 0 \\ a \cdot x = - b \\ x = \dfrac{-b}{a} \]

Com isso, temos uma expressão para encontrar as raízes de qualquer função afim. E não se preocupe, não precisa decorar essa fórmula, pois você sempre pode realizar o processo de isolar o $x$ (foi o que fizemos acima, porém sem números, de forma geral).

Mas e se $a = 0$? Bem, para realizar o processo acima, precisamos necessariamente que o $a$ seja diferente de 0, pois, caso ele seja igual a zero, teremos a seguinte situação: considere $a = 0$ e $b = -4$. Ao realizarmos o processo que descrevemos acima, chegaremos na seguinte equação:

\[ x = \dfrac{4}{0} \]

Agora, preciso perguntar a você: podemos dividir por 0? Se sua resposta for sim, tente dividir 4 balas entre 0 amigos, quantas balas cada amigo irá receber? Não tem como, né? Ou seja, não podemos dividir por 0.

Função constante e função nula

Quando nosso $a$ é igual a 0, dizemos que essa função é constante. Graficamente, ela será paralela ao eixo $x$, então só "terá" raízes se $b$ também for 0, ou seja, a função nula, que é igual a 0 para qualquer valor de $x$.

Gráfico mostrando função constante do primeiro grau. Reta horizontal cruza o número dois no eixo y — Função constante

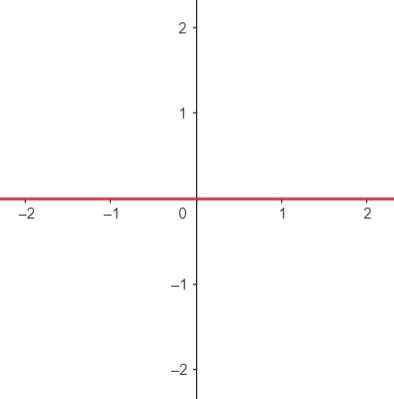
Gráfico mostra representação da função nula do primeiro grau, mostrando reta horizontal na direção do eixo y e x zero — Função nula

Para finalizar, observe a imagem a seguir.

Representação de reta vertical no plano cartesiano paralela ao eixo y, cortando o número 2 positivo no eixo x

Na sua opinião, essa reta é uma função afim? Enquanto você reflete sobre o que perguntei, vamos relembrar o que é uma função em si:

Uma função é uma relação entre dois conjuntos, $A$ e $B$, denotada por $f: A \rightarrow B$ que obedece duas propriedades:

1. Todo elemento de $A$ está ligado a algum elemento de $B$, ou seja, ninguém fica de fora em $A$;
2. Cada elemento de $A$ se liga de forma única a alguém em $B$

Feitas essas considerações, vamos à resposta da pergunta que fiz aí em cima. Observe que a reta não existe para nenhum outro ponto além do $x = 2$, e não é esse nosso problema. Nosso verdadeiro problema está em termos infinitos números em $y$ associados ao coitado do 2 que tem que carregar o peso do mundo inteiro nas costas.

Termos infinitos números ligados a um único $x$ contraria nossa segunda observação, que diz que cada $x$ se liga de forma única a algum $y$. Portanto, essa reta não é uma função. Na verdade, essa reta é uma "curva", mas isso será cena para as próximas publicações!

Resumo

A função real do primeiro grau é definida por $f: \mathbb{R} \rightarrow \mathbb{R}$, onde $f(x) = a \cdot x + b$ é representado graficamente por uma reta;
Na função afim, dois pontos definem uma única reta. E o $a$ é diferente de 0;
A função linear é um caso particular da função do primeiro grau, onde $b = 0$;
Na função constante, $a = 0$. Ou seja, $f(x) = b$;
$a$ é o coeficiente angular, pois está diretamente relacionado ao ângulo que o gráfico forma com o eixo $x$;
$b$ é o coeficiente linear ou termo independente. Ele informa onde a reta corta o eixo $y$;
$f: \mathbb{R} \rightarrow \mathbb{R}$ é uma função crescente se, para cada $x_0, x_1 \in \mathbb{R}$ tal que $x_0 < x_1$, temos que $f(x_0) < f(x_1)$;
Uma função é decrescente quando para $x_0 < x_1 $ reais, temos que $f(x_0) > f(x_1)$;
A expressão \[ a \cdot x + b = 0 \] é usada para encontrar as raízes de qualquer função afim;
Quando $a$ é igual a 0, dizemos que essa função é constante. Graficamente, ela será paralela ao eixo $x$, então só "terá" raízes se $b$ também for 0, ou seja, a função nula, que é igual a 0 para qualquer valor de $x$.

Como a função do primeiro grau aparece no Enem e nos vestibulares

Mão na massa! Agora é sua vez de colocar em prática tudo que aprendeu neste artigo. Então, papel e caneta na mão pra resolver os exercícios propostos e ver alguns exemplos de como a função do primeiro grau pode aparecer nos vestibulares.

Exemplo 1

(Unisinos 2017) João e Pedro alugaram o mesmo modelo de carro, por um dia, em duas locadoras distintas. João alugou o carro na locadora Arquimedes, que cobra R$ 80,00 a diária, mais R$ 0,70 por quilômetro percorrido. Pedro alugou na Locadora Bháskara, que cobra R$ 50,00 a diária, mais R$ 0,90 por quilômetro percorrido. Ao final do dia, João e Pedro pagaram o mesmo valor total pela locação.

a) 150 km e R$ 185,00

b) 160 km e R$ 192,00

c) 170 km e R$ 199,00

d) 180 km e R$ 206,00

e) 190 km e R$ 213,00

Resposta: [A]
Se n é o número de quilômetros rodados, então
\[ 0,9\cdot n + 50 = 0,7 \cdot n + 80 \ \Leftrightarrow 0,2 \cdot n = 30 \\ \Leftrightarrow n = 150km \]
Além disso, cada um pagou $0,9 \cdot 150 + 50 = R$ 185,00$
Assim, a resposta correta é a alternativa A.

Exemplo 2

(Enem 2016 - 2ª Aplicação) Um produtor de maracujá usa uma caixa d’água, com volume $V$, para alimentar o sistema de irrigação de seu pomar. O sistema capta água através de um furo no fundo da caixa a uma vazão constante. Com a caixa d’água cheia, o sistema foi acionado às 7h da manhã de segunda-feira. Às 13h do mesmo dia, verificou-se que já haviam sido usados 15% do volume da água existente na caixa. Um dispositivo eletrônico interrompe o funcionamento do sistema quando o volume restante na caixa é de 5% do volume total, para reabastecimento.

Supondo que o sistema funcione sem falhas, a que horas o dispositivo eletrônico interromperá o funcionamento?

a) Às 15h de segunda-feira

b) Às 11h de terça-feira

c) Às 14h de terça-feira

d) Às 4h de quarta-feira

e) Às 21h de terça-feira

Resposta: [E]
A taxa de variação do volume de água presente na caixa d'água é dada por
\[\dfrac{0,85−1}{13−7} = − 0,025 \]
Logo, se $p(t) = 1 − 0,025 \cdot t$ é a porcentagem do volume inicial de água, presente na caixa-d’água, após $t$ horas, segue que o dispositivo interromperá o funcionamento do sistema após um tempo $t$ dado por
\[0,05 = 1 − 0,025 \cdot t \Leftrightarrow t = 38 h\]
Portanto, como o sistema foi acionado às 7h da manhã de segunda-feira, a interrupção se dará às 21h de terça-feira.

Exemplo 3

Ana e Beatriz caminham em uma pista retilínea, na mesma direção e sentido, e com as respectivas velocidades constantes. Sabe-se que a posição de Ana, $P_A$, é dada por $P_A(t) = 200 + 25t$, que a posição de Beatriz, $P_B$, é dada por $P_B (t) = 500 + 20t$ e que o tempo $t$ é dado em minutos. Nessas condições, o tempo que Ana precisa para alcançar Beatriz é:

a) 60 minutos.

b) 45 minutos.

c) 25 minutos.

d) 20 minutos.

e) 40 minutos.

Resposta: [A]
Basta apenas igualar as funções para encontrar os pontos em comum. Assim:
\[ 200 + 25t = 500 + 20t \\ 5t = 300 \\ t = 60 \]
Com isso, Ana precisa de 60 minutos para alcançar Beatriz.

Conte com a ajuda dos melhores professores e de um conteúdo didático completo para se preparar para o Enem e outros vestibulares. Conheça a plataforma do Aprova Total!