Regra de três: simples, composta, como calcular e exercícios

A mais amada por todos os vestibulandos, aquela salvação no momento de desespero... Estamos falando da gloriosa regra de três, seja ela simples ou composta. Pode parecer favoritismo, mas não existe um vestibular que não cobre a famigerada regra de três! E para quem faz a prova do Exame Nacional do Ensino Médio (Enem) é mais importante ainda, pois é o assunto de maior incidência em Matemática.

Vamos explicar de forma simples o que é e como funciona a regra de três, para que você entenda como usar essa ferramenta incrível nas provas e nas continhas do dia a dia.

Usando a regra de três

Indo direto ao ponto, a regra de três é uma ferramenta matemática que nos ajuda a encontrar um valor desconhecido com base em pelo menos outros 3 valores que já conhecemos. Mas não podem ser quaisquer 3 valores, pois a regra de três só funciona se esse valores estiverem relacionados a grandezas proporcionais.

Exemplo: sabendo que para cozinhar 1 xícara de arroz são usadas 2 xícaras de água quente, para descobrir quantas xícaras de água são necessárias no cozimento de 3 xícaras de arroz você pode usar regra de três. Isso acontece porque as quantidades de água e arroz são proporcionais, quanto mais arroz para cozinhar, mais água vai precisar.

Por outro lado, sabendo que essa mesma xícara de arroz leva 12 minutos para cozinhar em fogo baixo, se você tentar usar uma regra de três para descobrir quanto tempo é necessário para o cozimento de 3 xícaras de arroz, o resultado seria 36 minutos.

🚨 Atenção: não faça esse teste em casa, você pode queimar o arroz e sua panela deixando 3 xícaras de arroz por 36 minutos no fogo!🚨

Mas por que não funciona? 😭

Lembra que regra de três só serve se as grandezas forem proporcionais? Pois é, a quantidade de arroz não é proporcional ao quantidade do tempo de cozimento, ou seja, não é possível usar regra de três. Nesse caso, o tempo de 12 minutos é fixo, para uma, duas, três, quantas xícaras de arroz couberem na panela, é uma quantidade constante.

Então, com essa ideia em mente, vamos conhecer os tipos de regra de três, como diferenciar os casos e resolver alguns exercícios para colocar seus conhecimentos em prática.

Ah! Antes de começarmos, é essencial conhecer um assunto conectado ao funcionamento da regra de três: razão e proporção. Leitura importante, hein?

Tipos de regra de três: simples e composta

Podemos definir a regra de três como uma relação entre duas ou mais grandezas proporcionais, lembrando que, se uma grandeza é alterada, as outras também se alteram.

No caso em que temos só duas grandezas envolvidas, chamamos de regra de três simples. Já nos casos em que temos três grandezas ou mais, chamamos de regra de três composta. Vamos explicar detalhadamente a seguir, mas é essencial lembrar que as relações se estabelecem com a grandeza que queremos descobrir.

Como estamos trabalhando com grandezas proporcionais, e proporção é uma igualdade entre duas razões, vejamos um exemplo antes de nos aprofundarmos em cada tipo de regra de três.

A razão é relação de uma grandeza (número) com outra grandeza, que pode ser expressa por meio de uma fração. Dessa forma, podemos usar a regra de três relacionando grandezas para encontrar o valor de uma incógnita.

Considere a situação em que, para fazer uma viagem de carro curta, abastecemos 12 litros de combustível e pagamos R$ 69,60. Para outra viagem mais longa, o plano é abastecer 18 litros no mesmo posto. Com essas informações, podemos estabelecer uma razão, para descobrir quanto vai custar a nova viagem:

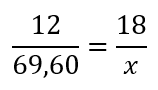
Uma forma de dar sentido à fração que montamos é pela leitura. Dizemos que 12 litros estão para 69,90 reais, assim como 18 litros estão para 𝑥 reais. Isolando o 𝑥 e fazendo uma multiplicação cruzada, encontraremos 104,40 reais.

A razão estabelecida entre grandezas é o que nos diz se elas são diretamente proporcionais ou inversamente proporcionais. Em cada um dos tipos de regra de três vamos aprender como identificá-las, qual a classificação das grandezas e quais as suas diferenças.

👉 Leia também:

Porcentagem: o que é, como calcular e exercícios resolvidos

Geometria espacial: tudo o que você precisa saber

Regra de três simples

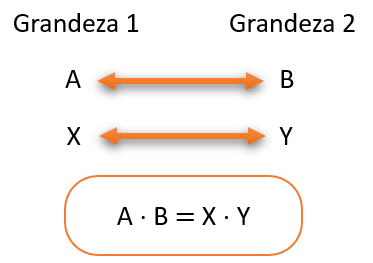
Na regra de três simples, quando a relação entre as grandezas é diretamente proporcional, multiplicamos cruzado. Por outro lado, quando as relações forem inversamente proporcionais, a técnica é diferente, será necessário multiplicar em linha.

Mas o que exatamente quer dizer grandezas diretamente proporcionais? Isso significa que, se uma grandeza aumentar a outra irá aumentar, e se uma grandeza diminuir a outra diminui também. Outra forma de pensar é que ambas as grandezas têm o mesmo comportamento, ou seja, aumentam juntas ou diminuem juntas.

Mas, em geral, para ajudar na resolução dos problemas, usamos setas no mesmo sentido para identificar uma relação como diretamente proporcional; e, para formular a equação, fazemos uma multiplicação cruzada, observe:

Regra de três simples - Diretamente proporcional

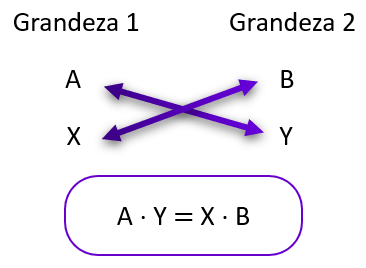
E como identificar uma relação inversamente proporcional? Esses são os casos em que, se uma grandeza aumentar a outra vai diminuir, e vice versa. Uma segunda forma de pensar é que, as grandezas têm comportamentos opostos, ou seja, obrigatoriamente são diferentes.

Para identificar essa proporção, usamos setas que apontam para sentidos opostos. Mas, para formular a equação, fazemos uma multiplicação em linha, observe:

Regra de três simples - Inversamente proporcional

Só existem essas duas possibilidades de classificação para uma regra de três simples, porque são apenas duas grandezas envolvidas.

Regra de três composta

Na regra de três composta existem pelo menos três grandezas envolvidas e a análise para saber se elas são diretamente ou inversamente proporcionais acontece por pares. O par é sempre formado pela grandeza que tem a incógnita, aquele valor que você quer descobrir, e outra das grandezas.

Assim como na regra de três simples, usamos setas no mesmo sentido, se as grandezas forem diretamente proporcionais, e setas em sentido oposto, se as grandezas forem inversamente proporcionais.

Para um exemplo genérico, considere as grandezas 1, 2 e 3, em que a incógnita faz parte da grandeza 1, simbolizada pelo clássico X. Organizando nossa regra de três composta em colunas, ficaria assim:

Os pares analisados se constituem da grandeza 1 e cada uma das outras grandezas separadamente, ou seja, primeiro analisamos a relação entre a grandeza 1 e 2, em seguida entre a grandeza 1 e 3. Suponha que as grandezas 1 e 2 são diretamente proporcionais, então sinalizamos com duas setas no mesmo sentido:

Agora, deixando de lado essa primeira análise, vamos olhar para a relação entre as grandezas 1 e 3. Suponha que elas são inversamente proporcionais, então sinalizamos com duas setas em sentidos opostos:

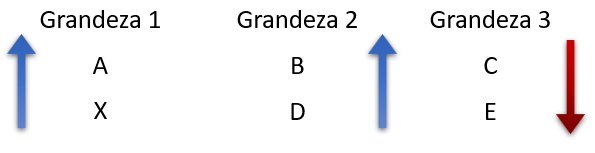
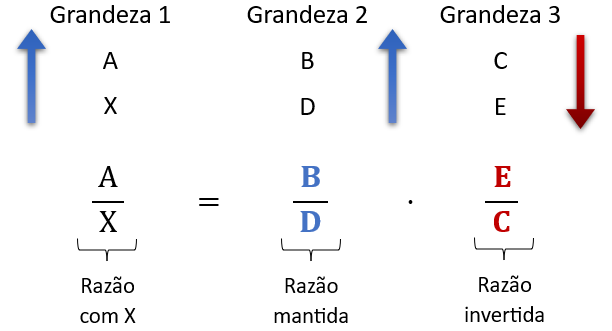
Existem muitas maneiras de montar a regra de três composta depois de relacionar as grandezas, mas vamos utilizar a mais direta. Copiamos a razão da grandeza que tem o X na ordem que aparece e igualamos ao produto das demais razões das grandezas, respeitando o seguinte critério:

• se a grandeza for diretamente proporcional, a razão deve ser mantida;
• se a grandeza for inversamente proporcional, a razão deve ser invertida.

No exemplo apresentado, a regra de três montada ficaria da seguinte forma:

A partir desse ponto tudo se resume a operações com frações, e você vai precisar resolver as multiplicações e isolar o X. Lembre-se de que as multiplicações de frações são feitas em linha e, tendo uma igualdade em duas frações, você sempre pode multiplicar cruzado. Então, finalizando o exemplo, para encontrar o valor de X seguimos esses passos:

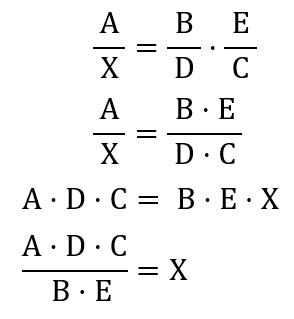
Você pode estar se perguntando: "E a relação entre a grandeza 2 e a 3, não importa?"

Na realidade, é exatamente isso! 😅

Analisamos apenas as relações em que aparece a grandeza 1, porque é nela que está a incógnita. Por isso, não nos interessa descobrir qual a relação entre as outras grandezas.

Em problemas com mais grandezas, o raciocínio é o mesmo. A grandeza que tem o valor que você quer descobrir precisa ser comparada com todas as outras, e a montagem terá mais frações para multiplicar.

Diferenças entre os tipos e classificações de regra de três

Agora que você conhece os dois tipos de regra de três, simples e composta, e as suas classificações, diretamente ou inversamente proporcional, vamos elencar as principais diferenças entre elas como a quantidade de grandezas envolvidas:

• a regra de três simples sempre relaciona duas grandezas proporcionais.
• a regra de três composta relaciona no mínimo três grandezas proporcionais.

Já a diferença entre regras de três diretamente e inversamente proporcional está na relação entre as grandezas. Lembrando que as relações sempre se estabelecem em pares de grandezas, em que uma delas tem a incógnita:

• a relação é diretamente proporcional se duas grandezas crescem juntas ou diminuem juntas.
• a relação é inversamente proporcional se uma grandeza cresce e a outra diminui.

Resumo e exemplos de regra de três simples

Utilizamos a regra de três simples quando há duas grandezas proporcionais e existe um valor desconhecido relacionado a uma das grandezas:

• Se as grandezas forem diretamente proporcionais, elas tem o mesmo comportamento e você deve multiplicar cruzado para encontrar o valor desconhecido.
• Se as grandezas forem inversamente proporcionais, elas tem comportamentos opostos e você deve multiplicar em linha para encontrar o valor desconhecido.

Exemplo diretamente proporcional: se 4 litros de tinta pintam uma parede de 6 metros quadrados, quantos litros vão pintar uma parede de 15 metros quadrados?

Neste caso, como as grandezas são diretamente proporcionais, devemos multiplicar cruzado, ou seja:

4 ⋅ 15 = 𝑥 ⋅ 6____→____𝑥 = 60/6____→____𝑥 = 10

Concluímos que serão necessários 10 litros de tinta pintar uma parede de 15 metros quadrados.

Exemplo inversamente proporcional: se 10 trabalhadores constroem uma casa em 20 dias, quantos trabalhadores serão necessários para construir a mesma casa em 40 dias?

Neste caso, como as grandezas são inversamente proporcionais, devemos multiplicar em linha, ou seja:

10 ⋅ 20 = 𝑥 ⋅ 40____→____𝑥 = 200/40____→____𝑥 = 5

Concluímos que serão necessários 5 trabalhadores para construir a casa em 40 dias.

👉 Leia também:

Juros compostos: veja como calcular, fórmulas e exemplos práticos

Vença o medo da Matemática com essas dicas de estudo

Resumo e exemplos de regra de três composta

Utilizamos a regra de três composta quando há três ou mais grandezas proporcionais e existe um valor desconhecido relacionado a uma dessas grandezas. Além disso, é importante lembrar que, para classificar a relação entre as grandezas como diretamente ou inversamente proporcional, a grandeza que tem a incógnita sempre deve estar envolvida.

Para resolver a regra de três composta, depois de identificar as grandezas, você pode fazer o seguinte processo:

• escreva a razão da grandeza que contém a incógnita e escreva o sinal de igual;
• do outro lado da igualdade escreva uma multiplicação entre as razões, em que a razão é mantida se a relação for diretamente proporcional ou invertida se a relação for inversamente proporcional.

Exemplo inversamente proporcional: um açougue frigorífico cobra R$ 5.200 para transportar 1.300 kg de carne para uma cidade que fica a 300 km de distância. Em outra cidade, um comerciante, dispondo de R$ 3.000, deseja comprar a quantidade máxima de carne que conseguir. Sabendo que a distância da sua loja até o frigorífico é de 200 km, qual a quantidade de carne que ele poderá encomendar sem exceder seu orçamento?

Utilize as setas para indicar as relações entre cada grandeza, para em seguida montar as razões:

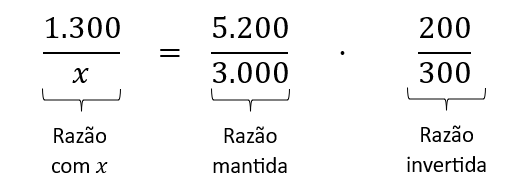
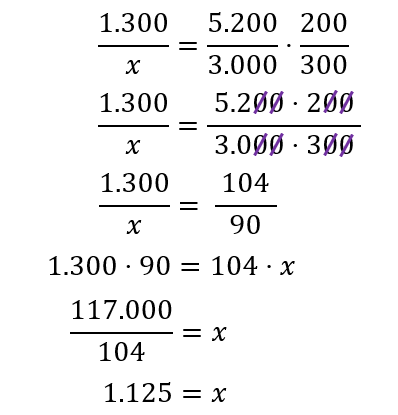
Concluímos que a quantidade de carne que ele poderá encomendar é de 1.125 kg.

Como a regra de três aparece no Enem e nos vestibulares?

Infelizmente, não há um tipo de regra de três favorita, nem para o Enem, nem para outros vestibulares.

Assim, para se garantir, é importante estudar todas: regra de três simples, composta, diretamente proporcional e inversamente proporcional. O que costuma acontecer nas questões de Enem e vestibulares é que existem modelos de resoluções parecidos.

Os vestibulares que cobram regra de três simples podem apresentar os dados de forma que você vai precisar somar ou multiplicar alguns valores antes de montar sua regra de três. Os casos que envolvem soma costumam falar sobre aumento direto/bruto e os casos de multiplicação costumam falar sobre aumento percentual ou porcentagem.

Por outro lado, os que cobram regra de três composta, normalmente, trazem 3 ou 4 grandezas nem sempre explícitas. Então, ligue o alerta para enunciados que falam sobre triplicar eficácia, dobrar produção ou cair pela metade, essas palavras costumam indicar uma relação entre grandezas implícita.

No Enem, a regra de três costuma ser parte da resolução, em que você vai precisar fazer algo além dela, manipular um pouco mais o resultado ou trabalhar com conversões de unidade de medida ao longo da resolução.

Regra de três simples no vestibular

TEXTO PARA A PRÓXIMA QUESTÃO

Casos de febre amarela desde o início de 2017:
confirmados → 779
suspeitos → 435
Mortes entre os casos confirmados: 262

(Uerj 2019)  Suponha que todos os casos suspeitos tenham sido comprovados, e que a razão entre o número de mortes e o de casos confirmados permaneça a mesma.
Nesse caso, com as novas comprovações da doença, o número total de mortos por febre amarela estaria mais próximo de: 

a) 365  
b) 386 
c) 408  
d) 503  

Resposta: [C]
Considerando que a razão entre o número de mortes e o de casos confirmados permaneça a mesma, podemos utilizar essas grandezas para montar uma regra de três. Analisando a relação entre as grandezas, quanto maior o número de casos, maior o número de mortes, ou seja, elas são diretamente proporcional.

Sabemos que, inicialmente, foram registrados 779 casos, dos quais resultaram 262 mortes e 435 casos suspeitos. A questão diz que todos os casos suspeitos foram confirmado, ou seja, precisamos somar esses 435 casos aos 779 que já estavam comprovados, resultando em 1.214 casos comprovados.

Agora podemos montar a regra de três em busca do número aproximado de mortes:

________Casos comprovados_________Número de mortes
_________________779_______________________262
________________1.214_______________________𝑥

Como temos uma regra de três simples diretamente proporcional, basta multiplicar cruzado:

779𝑥 = 1.214 ⋅ 262___→___ 𝑥 = 318.068/779___→___ 𝑥 = 408,3

O problema pedia um número próximo, por isso podemos arredondar o valor encontrado para 408.

Regra de três composta no vestibular

(PUCPR 2018 - Adaptada) Uma máquina produz um único tipo de peça, operando sempre, por motivos de segurança, apenas e exatamente 12 horas/dia, ininterruptamente, inclusive aos sábados, domingos e feriados. Essa máquina será substituída por outra com a capacidade de produzir o quádruplo da quantidade de peças, em um mesmo período de tempo. A nova máquina vai operar, ininterruptamente, por 21 horas a cada dia, todos os dias da semana. Durante quantos dias, no mínimo, a nova máquina precisará operar para produzir o triplo do que a antiga produz em uma semana?

a) 1 dia
b) 3 dias
c) 4 dias
d) 5 dias
e) 6 dias

Resposta: [B]
Identificamos duas grandezas: horas por dia e quantidade de dias. Além delas, temos a capacidade (c), que quadruplicou, e a produção (p), que precisa triplicar:

_Hora p/ dia_________Dias________Capacidade (c)______Produção (p)
______12______________7 _______________c__________________p
______21______________𝑥_______________4cc________________3p

Analisando a relação das grandezas com a quantidade de dias:
1ª - quanto maior a quantidade de dias, menor será a quantidade de horas/dia operando → Inversamente proporcional
2ª - quanto maior a quantidade de dias, menor será a capacidade de produção → Inversamente proporcional
3ª - quanto maior a quantidade de dias, maior será a produção de peças → Diretamente proporcional


Montamos a equação da regra de três invertendo as grandezas inversamente proporcionais e mantendo as diretamente proporcionais:

Resolvendo a equação:

Regra de três no Enem

(Enem 2022) Um borrifador de atuação automática libera, a cada acionamento, uma mesma quantidade de inseticida. O recipiente desse produto, quando cheio, contém 360 mL de inseticida, que duram 60 dias se o borrifador permanecer ligado ininterruptamente e for acionado a cada 48 minutos.
A quantidade de inseticida que é liberada a cada acionamento do borrifador, em mililitro, é

a) 0,125.  
b) 0,200. 
c) 4,800.
d) 6,000.
e) 12,000.

Resposta: [B]
Para resolver o problema, você pode descobrir quantas borrifadas foram dadas até o borrifador esvaziar e. em seguida, dividir pela quantidade de inseticida que tinha nele. Montando uma regra de três para descobrir o número de borrifadas até acabar o inseticida, temos que:

_Borrifadas________Tempo________________________________Borrifadas________Tempo
______1___________48 min ______Convertendo dias______________1______________48 min
______𝑥___________60 dias_________para minutos________________𝑥_____________60 ⋅ 24 ⋅ 60 min

Antes de analisar se a regra de três é diretamente ou inversamente proporcional, o tempo precisava estar em uma mesma unidade de tempo. A escolha foi de transformar os 60 dias em minutos, essa conversão foi feita de forma que:
- como um dia tem 24 horas, multiplicamos o número de dias por 24
- em seguida, como uma hora tem 60 minutos, multiplicamos o número de horas por 60

Agora analisando as grandezas, quando aumentamos a quantidade de borrifadas, aumenta também a quantidade de tempo, por isso, as grandezas são diretamente proporcionais. Resolvendo a regra de três multiplicando cruzado, temos:

48𝑥 = 60 ⋅ 24 ⋅ 60___→___ 𝑥 = (60 ⋅ 24 ⋅ 60)/48___→___ 𝑥 = 1.800

Então, ao longo de 60 dias, foram 1.800 borrifadas, dividindo os 360 mL por 1.800 borrifadas, encontramos que cada borrifada libera 0,2 mL de inseticida.