Geometria espacial: tudo o que você precisa saber
Reunimos tudo o que você precisa conhecer para dominar essa dimensão matemática. Dos conceitos básicos até os mais avançados, confira os princípios, formas e propriedades dos sólidos geométricos

Acessibilidade
A geometria espacial é uma fascinante área da Matemática que estuda as formas e as relações no espaço tridimensional. Suas aplicações no cotidiano são vastas e surpreendentes, permeando diversos aspectos da nossa vida.
Ou seja, desde a arquitetura, com a elaboração de projetos e construção de edifícios, até a engenharia, a geometria espacial desempenha um papel indispensável na criação de estruturas sólidas e eficientes.

Além disso, a geometria espacial está presente no design de objetos, no planejamento de rotas de tráfego, no cálculo de volumes de embalagens e até mesmo nas aplicações tecnológicas, como modelagem 3D e realidade virtual, que revolucionaram a forma como interagimos com o mundo.
Por meio do estudo da geometria espacial, é possível não apenas apreciar a beleza das formas tridimensionais, mas também compreender a essência matemática que permeia o ambiente físico, aprimorando o uso do espaço em benefício prático e estético. Vamos mergulhar na geometria espacial, o 3º assunto que mais aparece no Exame Nacional do Ensino Médio (Enem)?
NAVEGUE PELOS CONTEÚDOS
O que se estuda em geometria espacial?
Geometria espacial é o campo da Matemática que estuda as figuras no espaço e suas propriedades. Mas, diferente da geometria plana, que está limitada a duas dimensões, na geometria espacial trabalhamos com três dimensões. Assim, além do cálculo de áreas, podemos calcular o volume de sólidos geométricos, poliedros, pirâmides e entre outros.
Principais conceitos da geometria espacial
Para entender as formas geométricas espaciais é necessário ter uma compreensão das noções primitivas, interpretações fundamentais que serão a base para entender as figuras de três dimensões.
- Ponto: objeto que não possui dimensão e forma, portanto, não pode ser medido.
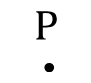
- Reta: conjunto de infinitos pontos alinhados, que tem dimensão, e é classificada como objeto unidimensional.
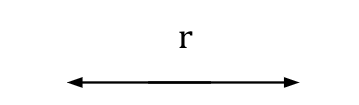
- Plano: conjunto de retas dispostas lado a lado, de modo que não haja espaços entre essas retas, e que ele também seja infinito, sendo classificado como objeto bidimensional.

- Espaço: extensão tridimensional dos eixos cartesianos que permite a análise e a descrição de formas, objetos e suas relações geométricas.
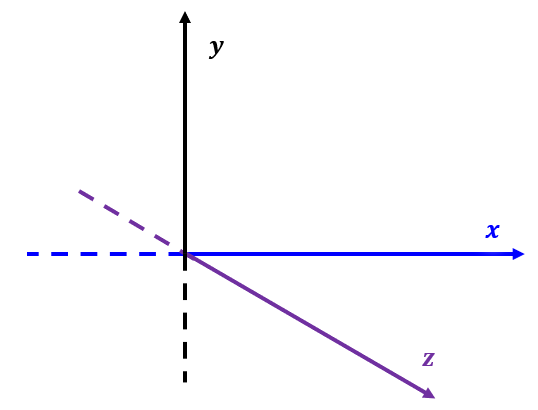
Os instrumentos que você viu até aqui serão utilizados para construir, aplicar e resolver problemas na geometria espacial. Então, é a partir deles que se enunciam teoremas e definições.
Geometria espacial e sólidos geométricos
Os sólidos geométricos são formas tridimensionais que possuem comprimento, largura e altura. Eles se caracterizam por suas faces, arestas e vértices, e cada um dos elementos desempenha papel importante na definição e identificação de cada um desses sólidos.
Arestas, vértices e faces
Vamos agora entender o que cada uma destas características representam.
- Face: polígonos planos que formam os sólidos.
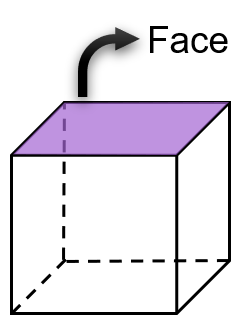
- Arestas: lados das faces do polígonos.
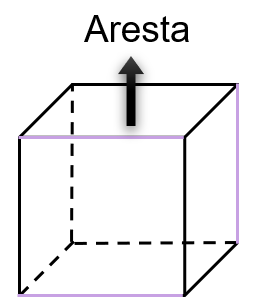
- Vértices: ponto em que as arestas se encontram.
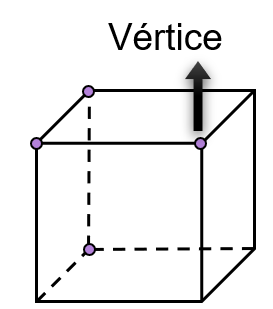
Poliedros e a relação de Euler
Poliedros são sólidos formados pela união de faces poligonais. No universo de todos os poliedros imagináveis, existem cinco poliedros especiais chamados de poliedros de Platão ou poliedros regulares. Os poliedros regulares são aqueles em que todas as faces são idênticas, faces estas que podem ser triangulares, quadradas ou pentagonais.
Vale a pena lembrar que as faces que compõe um poliedro regular são polígonos regulares, ou seja, triângulos equiláteros, quadrados e pentágonos regulares.
Veja a seguir os nomes, quantidade de faces e os formatos de cada poliedro regular.
- Tetraedro regular: poliedro regular com 4 faces triangulares. É o poliedro regular com o menor número de faces.
- Hexaedro regular (cubo):
poliedro regular com 6 faces quadradas.
- Octaedro regular:
poliedro regular com 8 faces triangulares.
- Dodecaedro regular: poliedro regular com 12 faces pentagonais.
- Icosaedro regular: poliedro regular com 20 faces triangulares. É o poliedro regular com o maior número de faces.
Dentre os poliedros convexos, existe uma importante relação entre o número de vértices (V), arestas (A) e faces (F) chamada de relação de Euler. Essa relação é expressa da seguinte maneira:
V + F = A + 2
Utilizando a relação de Euler podemos encontrar o número de uma das características de um poliedro convexo sabendo apenas outras duas, incrível não?
Exemplo da relação de Euler
Dado um poliedro regular e convexo cujo o número de vértices e o número de arestas são respectivamente 12 e 30, qual o nome do poliedro em questão?
Para descobrimos o nome de um poliedro regular, devemos saber a quantidade de faces que ele possui. Como já sabemos o número de vértices, o número de arestas e sabemos que é um poliedro convexo, podemos utilizar a relação de Euler para encontrar o número de faces. Desta forma, substituindo V = 12 e A = 30 na relação de Euler, temos que:
V + F = A + 2
12 + F = 30 + 2
12 + F = 32
F = 32 - 12
F = 20
Dessa forma, o poliedro em questão possui 20 faces, ou seja, é um Icosaedro.
Cubo
O hexaedro regular, mais conhecido como cubo, é um dos principais poliedros regulares, esse formato é comum em diversos objetos. Você com certeza já ouviu falar do cubo mágico, não é mesmo?
O cubo tem 6 faces quadradas, todas com ângulos retos de 90 graus e sua propriedade mais importante é que todas as suas arestas possuem a mesma medida. Essa característica torna relativamente simples descobrir as medidas da área lateral e do volume. Então, para realizar os cálculos, vamos considerar um cubo de aresta L, como na ilustração abaixo:
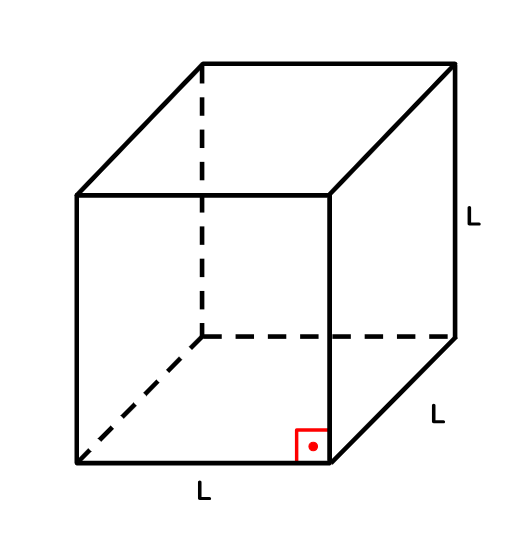
Para descobri o volume (V) de um cubo, basta utilizar a medida da sua aresta, no nosso caso L. Assim utiliza-se a fórmula:
\(V=L^3\)
Exemplo: um cubo de aresta medindo 5 cm tem um volume de 125 cm³.
A área total ( At ) de um cubo é a soma da área de cada uma das faces do cubo, como todas as 6 faces são iguais e possuem lados iguais, a área total do cubo é dada por:
\(A_t=6\cdot L^2\)
Exemplo: um cubo de aresta medindo 3 cm tem uma área total de 54 cm².
Diagonais do cubo
Outro característica importante do cubo são suas diagonais, existem duas diagonais importantes:
- Diagonais menores ou diagonal da face (d): a diagonal de uma face é um segmento que começa em um vértice e termina em outro vértice oposto a ele na mesma face, de modo que separa a face em duas partes iguais. Para encontrar o valor da sua medida basta utilizar o teorema de Pitágoras, em que os catetos são as arestas do cubo e a hipotenusa é a diagonal da face. Assim a medida da diagonal da face é
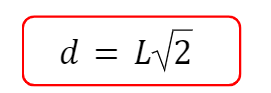
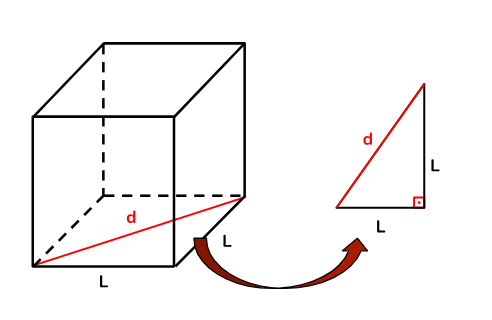
- Diagonais maiores ou diagonais internas (D): a diagonal interna é o segmento que une dois vértices de faces opostas percorrendo o interior do cubo. Para encontrar o valor da sua medida basta utilizar o teorema de Pitágoras, em que um dos catetos é a aresta do cubo, o outro é a diagonal face e a hipotenusa é a diagonal interna. Assim a medida da diagonal interna é
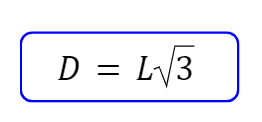
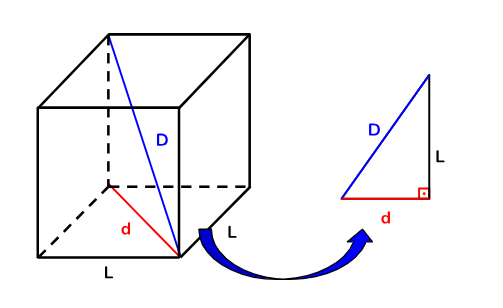
Paralelepípedo
O paralelepípedo é um sólido geométrico que possui 6 faces e todas são paralelogramos, isto é, polígonos de 4 lados com lados opostos paralelos. Além disso, o paralelepípedo pode ser reto ou oblíquo.
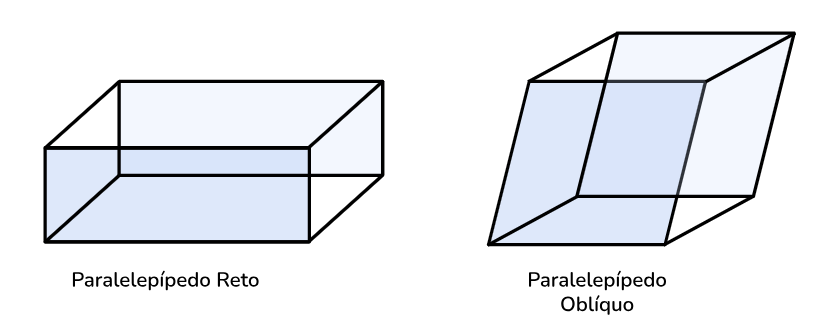
Com seis faces de paralelogramos, os formatos de paralelepípedo permitem que ele seja empilhado e encaixado facilmente em diferentes configurações, tornando-o ideal para a construção de estruturas e objetos.
Além disso, o paralelepípedo possui três pares de arestas paralelas e congruentes, o que o torna uma escolha popular para a criação de caixas, embalagens e objetos retangulares em geral.
As medidas de um paralelepípedo são: Comprimento (C), Largura (L) e Altura (H).
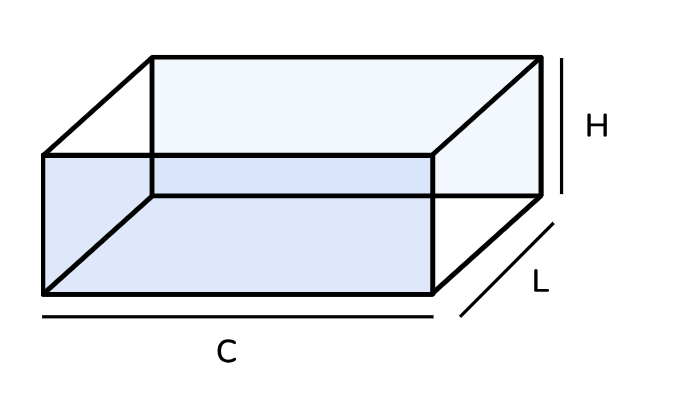
Com estas medidas, podemos estruturar as principais fórmulas do paralelepípedo.
Áreas e volume:
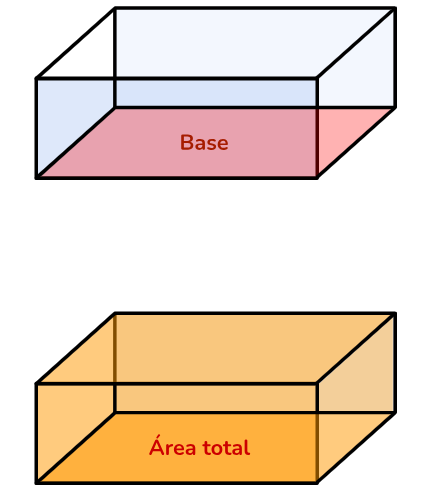
Área da base (Ab):
\(A_b = C \cdot L\)
Área total (At):
\(A_t = 2 \cdot C \cdot L + 2 \cdot C \cdot H + 2 \cdot L \cdot H\)
Volume (V):
\(V = C \cdot L \cdot H\)
Diagonais
Diagonal da face (d):
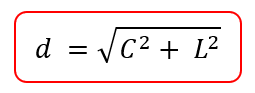
Diagonal Interna (D):

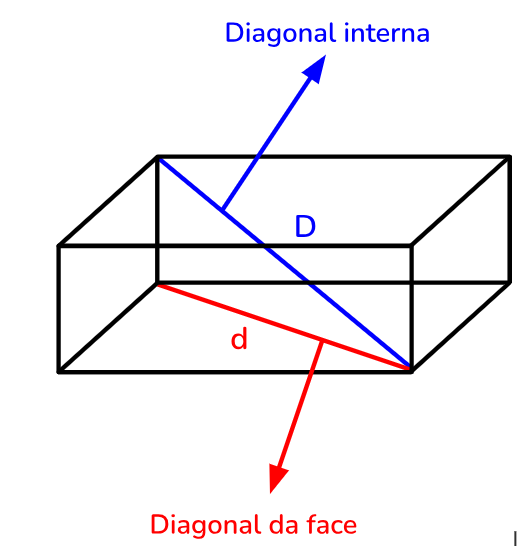
Observação importante: um cubo também é um paralelepípedo!!! 😲
Prisma
Um prisma é um sólido geométrico tridimensional que possui duas bases congruentes, conectadas por faces laterais planas. Essas faces laterais são sempre paralelogramos.
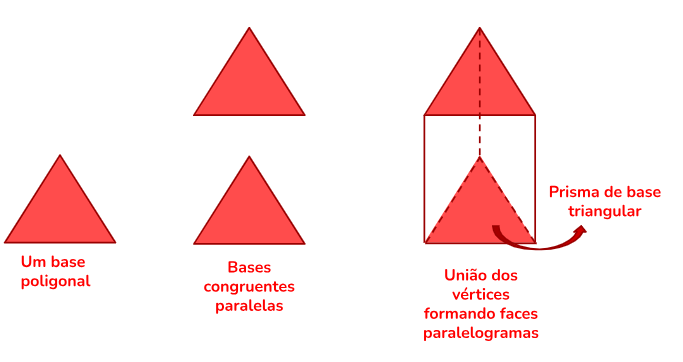
Uma das coisas mais fascinantes sobre os prismas é a sua ampla variedade de formas e configurações. Existem prismas retos, oblíquos, regulares e irregulares, cada um com suas particularidades. Essa diversidade oferece infinitas de possibilidades para a criação de estruturas e objetos com formas distintas.
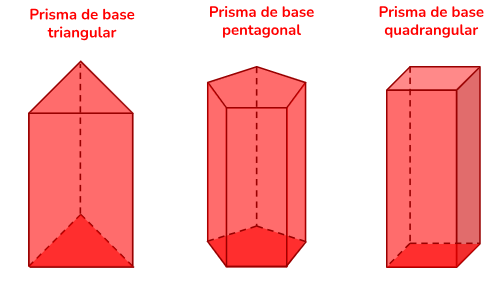
Os prismas podem ser classificados de acordo com a forma das suas bases. Alguns exemplos:
- prisma triangular
possui uma base em forma de triângulo e faces laterais que são paralelogramos.
- prisma pentagonal
possui uma base em forma de pentágono e faces laterais que são paralelogramos.
- prisma quadrangular (ou cuboide)
tem uma base quadrada ou retangular e faces laterais que também são quadrados ou retângulos.
Cada parte de um primas possui um nome, também chamados de elementos do prisma, e a partir deles podemos vamos calcular diversas medidas de um prisma.
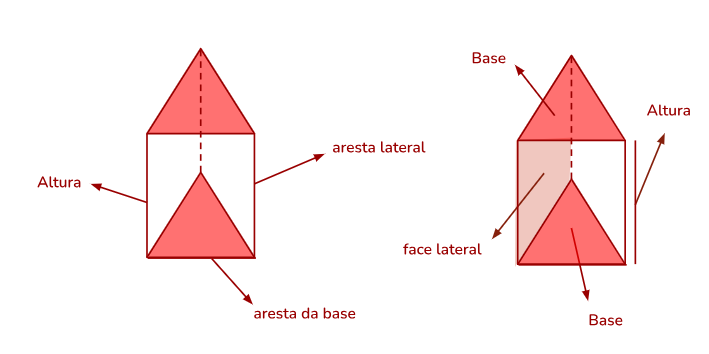
As fórmulas dos prismas regulares são utilizadas para calcular diversas propriedades desses sólidos geométricos. Considerando as variáveis número de arestas da base (n), aresta da base (a), altura (h) e área da base (Ab), seguem algumas fórmulas comuns relacionadas aos prismas:
- área lateral de um prisma (AL)
\(A_L = n \cdot h \cdot a\) - área total de um prisma (At)
\(A_t = 2 \cdot A_b + A_L\) - volume de um prisma (V)
\(V = A_b \cdot h\)
Observação importante: um cubo também é um prisma!!! 🤯
Pirâmide
Uma pirâmide é um sólido geométrico tridimensional que possui uma base poligonal e faces triangulares que se encontram em um ponto chamado vértice ou ápice.

A construção da pirâmide na Matemática é feita a partir de uma base poligonal: marcamos um ponto fora desta base e unimos os vértices da base com o ponto que está fora da base.
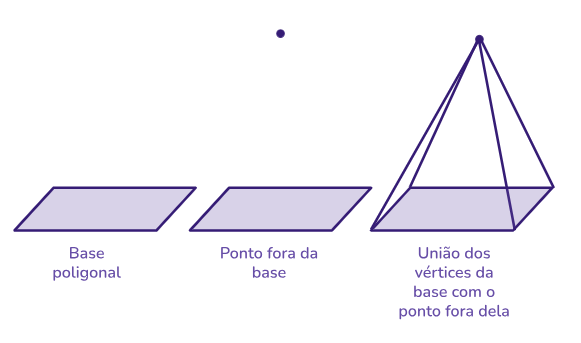
A base da pirâmide é um polígono, que pode ser triangular, quadrangular, pentagonal ou qualquer outra forma poligonal. Dessa maneira, a forma da base influencia na classificação da pirâmide.
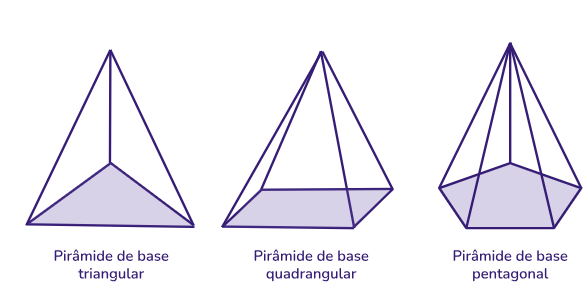
Similar aos prismas, as pirâmides são formadas por vários elementos importantes para realizar diversos cálculos. Vejamos os principais indicados nas duas figuras abaixo:
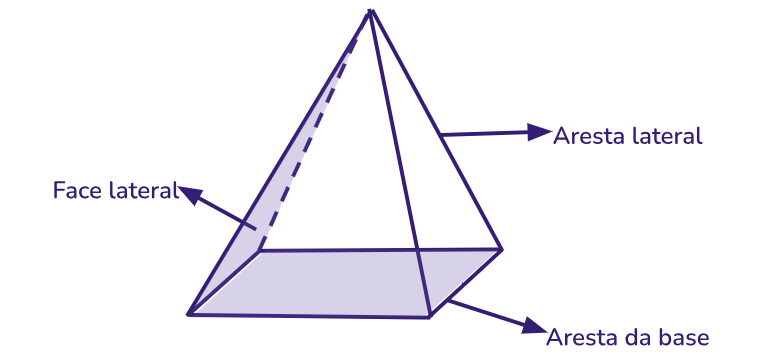
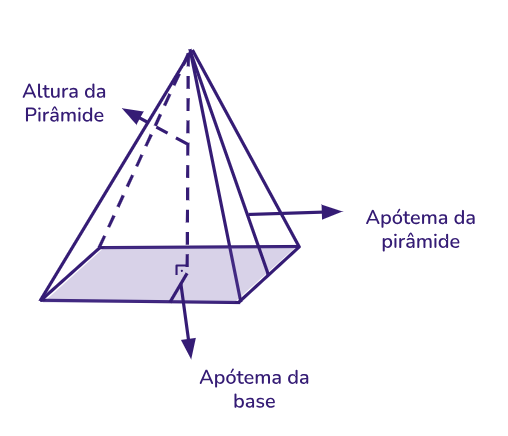
Cada um dos elementos acima é descrito na geometria espacial como:
- faces laterais
faces triangulares da pirâmide
- aresta lateral
segmento do vértice da base até o vértice da pirâmide
- aresta da base
segmento formado pela união dos vértices da base que são lados da base
- apótema da pirâmide
altura da face da pirâmide
- apótema da base
segmento que liga o centro da base até o ponto médio da aresta da base.
- altura da pirâmide
segmento do vértice da pirâmide ao plano da base a um ângulo de 90º.
Fórmulas para usar nos cálculos de pirâmides
Existem várias fórmulas relacionadas à pirâmides que podem ser úteis para calcular suas propriedades. Dentre elas:
- área da base de uma Pirâmide (Ab):
é calculada de acordo com a forma da base, ou seja, para base triangular a fórmula será uma, para base quadrada outra, para base hexagonal outra e assim por diante.
- área lateral da pirâmide (Al)
soma da área das faces laterais da pirâmide, para pirâmides retas regulares você pode calcular multiplicando o perímetro da base pelo apótema da base e dividir por 2.
- volume da pirâmide (V)
o volume da pirâmide é calculada multiplicando a área da base (Ab) pela altura (h) e dividindo por 3. Portanto, \(V=\dfrac{A_b\cdot h}{3}\)
- altura da pirâmide (h)
você pode utilizar o teorema de Pitágoras se conhecer as medidas das apótema da base e o apótema da pirâmide. Assim, com esses elementos, é possível formar um triângulo retângulo em que o apótema da base será um cateto, a altura da pirâmide será outro e a hipotenusa será o apótema da pirâmide:
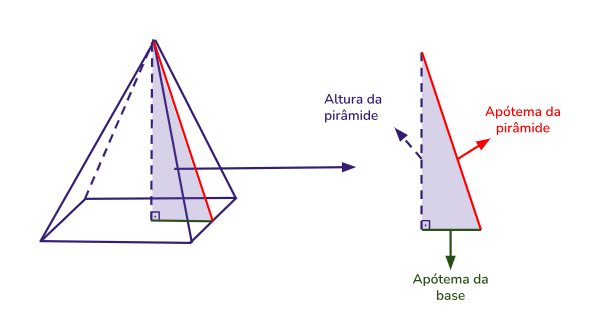
Denotando x como apótema da pirâmide e y como a apótema da base, temos que a altura h pode ser encontrada na expressão: \(x^2=h^2+y^2\)
Observação importante sobre as pirâmides: um cubo não é um pirâmide!!! 😭
Cilindro
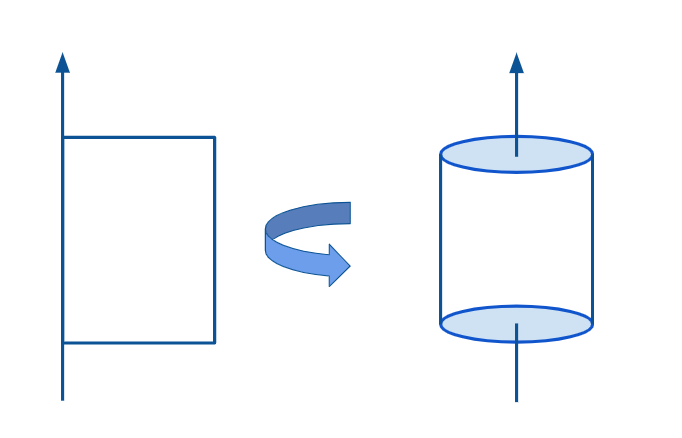
Um cilindro é um sólido de revolução que possui duas bases congruentes e paralelas, que são círculos, e uma superfície lateral curva que as conecta. Existem vários tipos de cilindros com base em suas características e propriedades. Um cilindro recebe o nome de sólido de revolução pois se forma a partir da rotação de um retângulo em torno de um eixo.
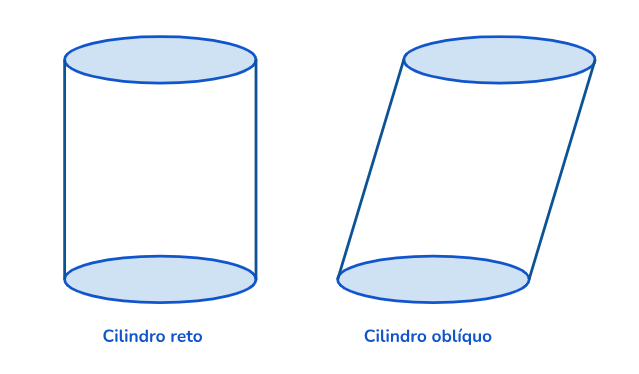
Alguns exemplos comuns incluem o cilindro reto e o cilindro oblíquo, apresentados abaixo:
Um cilindro não possui tantos elementos, porém é importante estar atento para as suas definições e saber identificar nas figuras onde estão localizados estes elementos.
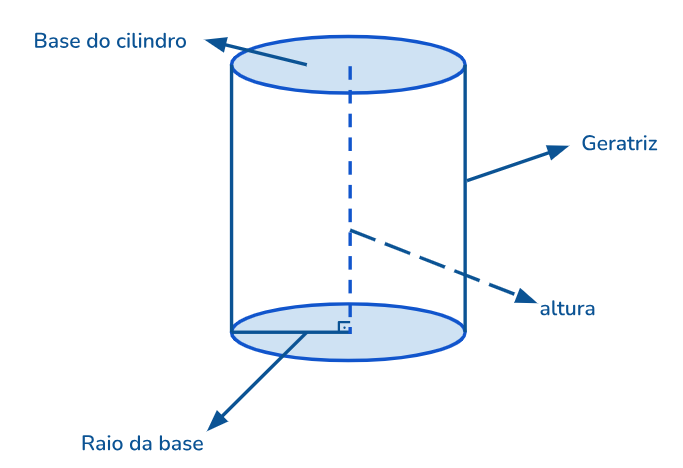
As base dos cilindros são sempre circulares e dependemos do raio para calcular sua área.
Área da base de um cilindro (Ab): \(A_b = \pi \cdot r^2 \), onde r é o raio da base.
Volume de um cilindro (V): para encontrar o volume de cilindro basta utilizar a área da base (Ab) e multiplicar pela altura (h). Portanto, \(V = A_b \cdot h\).
Para encontrar o valor da área lateral de um cilindro, precisamos ter uma visualização da sua planificação, pois ao planificar obtemos um retângulo e sabemos que o cálculo da sua área é base x altura.
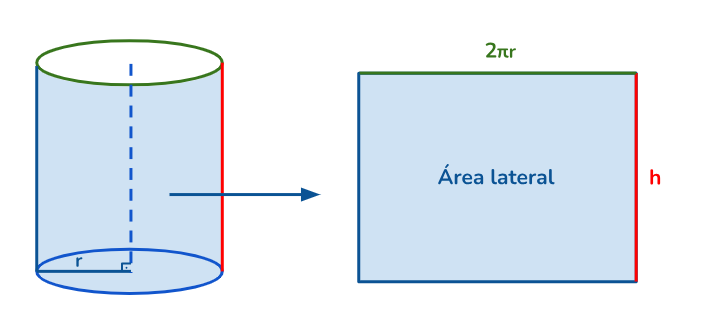
A base do retângulo é o comprimento da circunferência, que sabemos que pode ser calculado por \(2 \cdot \pi \cdot r\) e a altura do retângulo coincide com a altura do cilindro, logo a fórmula para calcular a área lateral (Al) de um cilindro reto é : \(A_l= 2 \cdot \pi \cdot r \cdot h\).
Não esqueça que, sabendo calcular a área da base e a área lateral, você já é capaz de saber calcular a área total (At): \(A_t = 2 \cdot A_b + A_l\)
Cone
O cone é uma figura geométrica tridimensional com base circular e um ponto chamado vértice, que se conecta todos os pontos da base por linhas retas chamadas geratrizes.
Essa forma distintiva do cone confere a ele propriedades geométricas peculiares e uma variedade de aplicações práticas. Um tipo de cone familiar é o cone de trânsito:

Assim como o cilindro, o cone também é um sólido de revolução, dessa maneira, se constrói a partir da rotação de um triângulo em torno de um eixo.
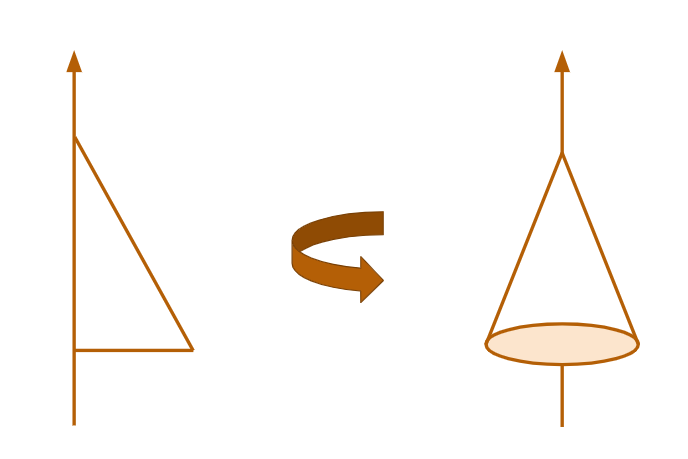
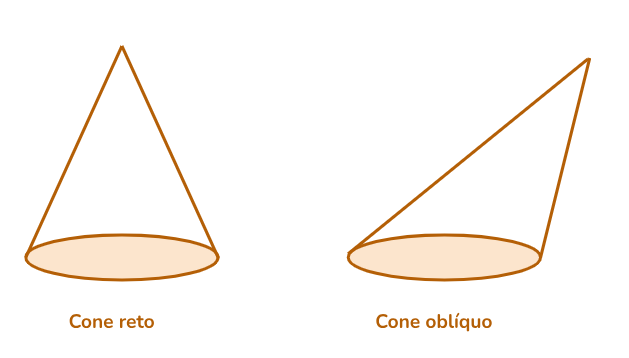
Os cones, dependendo da posição do eixo em relação à base, classificam-se em reto ou oblíquo, como ilustrado abaixo:
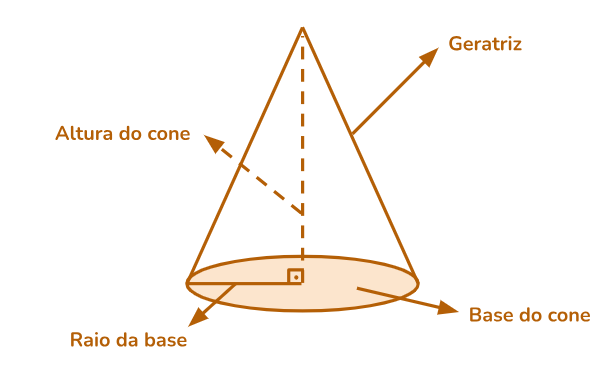
Os principais elementos que constituem um cone são a base, o vértice, a altura, a geratriz e o ângulo de abertura.
As bases do cone são sempre circulares, dessa forma para encontrar a sua área utiliza-se fórmula conhecida do da área do círculo.
Área da base de um cone (Ab): \(A_b = \pi \cdot r^2\) , onde r é o raio da base.
Volume de um cone (V): utilize a área da base (Ab) multiplicar pela altura (h) e dividir por 3. Portanto, V = (Ab · h)/3.
Cálculos relacionados ao cone
Para encontrar a geratriz de um cone, é necessário visualizar o triângulo retângulo, onde os catetos são o raio da base (r) e a altura do cone (h) e a hipotenusa é a geratriz (g).

Dessa forma, utilizando o teorema de Pitágoras temos que: \(g^2 = h^2 + r^2\)
Para encontrar o valor da área lateral de um cone, precisamos ter uma visualização da sua planificação, pois ao planificar obtemos um setor circular.
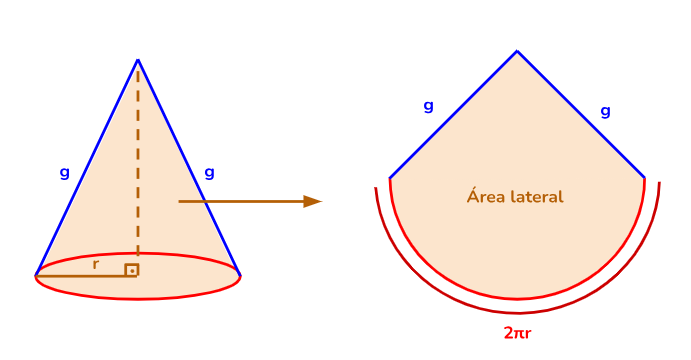
Para calcular a área lateral (Al) de um setor circular basta utilizar a fórmula: \(A_l = \pi \cdot r \cdot g\)
Similar ao cilindro, sabendo calcular a área da base do cone e a área lateral do cone, você já é capaz de saber calcular a área total (At): \(A_t = 2 \cdot A_b + A_l\)
Exercícios de geometria espacial do Enem e outros vestibulares
Confira alguns exercícios de geometria espacial resolvidos:
Exemplo 1
(Enem) Num recipiente com a forma de paralelepípedo reto-retângulo, colocou-se água até a altura de 8 cm e um objeto, que ficou flutuando na superfície da água.
Para retirar o objeto de dentro do recipiente, a altura da coluna de água deve ser de, pelo menos, 15 cm. Para a coluna de água chegar até essa altura, é necessário colocar dentro do recipiente bolinhas de volume igual a 6 cm³ cada, que ficarão totalmente submersas
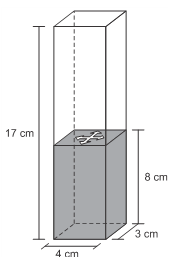
O número mínimo de bolinhas necessárias para que se possa retirar o objeto que flutua na água, seguindo as instruções dadas, é de
a) 14.
b) 16.
c) 18.
d) 30.
e) 34.
Resposta: [A]
Como o recipiente já estava com água até 8 cm de altura, só precisam aumentar 7 cm de altura para chegar aos 15 cm necessários para retirar o objeto. Para descobrir o mínimo de bolinhas que deve estar ali, primeiro precisamos calcular o volume correspondente ao aumento de 7 cm de altura do recipiente. Para encontrar esse valor basta multiplicar a área da base pela altura desejada, ou seja:
Ab ⋅ h = (3⋅4) ⋅ 7 = 84 cm³
Considerando que cada bolinha ocupa o volume de 6 cm³ e precisamos preencher o recipiente com no mínimo 84 cm³, chamando o número de bolinhas de b, temos a seguinte desigualdade:
6b ≥ 84 ⇔ b ≥ 14
Portanto, o número mínimo de bolinhas é 14.
Exemplo 2
(Uerj 2021) Um recipiente com a forma de uma pirâmide de base quadrada foi completamente preenchido com um líquido. Sua aresta da base mede 4 cm e a altura, 9 cm. Em seguida, todo esse líquido foi transferido para outro recipiente, com a forma de um prisma reto, sendo sua base um triângulo retângulo isósceles cujos catetos medem 4 cm. Observe as imagens:
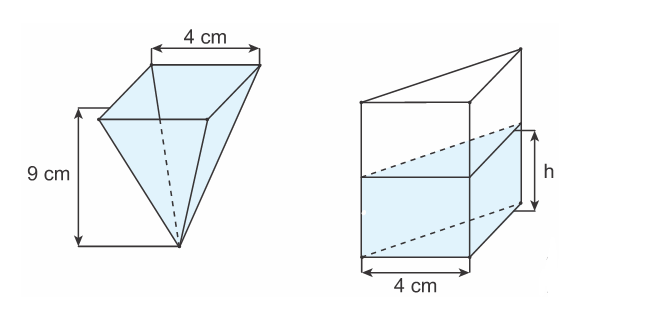
Considere que as espessuras dos recipientes são desprezíveis e que as bases estão em planos horizontais, sendo as alturas definidas em relação às bases.
A altura h, em centímetros, que o líquido atingirá no segundo recipiente é:
a) 10
b) 8
c) 6
d) 4
Resposta: [C]
O primeiro passo é calcular volume de líquido que está no recipiente em forma de pirâmide. Considerando que a base é um quadrado de lado 4 cm e a altura é 9 cm, temos que:
Vp = (1/3) ⋅ Ab ⋅ h = (1/3) ⋅ 4² ⋅ 9 = 4² ⋅ 3 cm³
O segundo recipiente tem forma de prisma de base triangular, sendo que o triângulo da base é retângulo isósceles com catetos de medida 4 cm. Então, se queremos descobrir a altura atingida no segundo recipiente, basta igualar o volume da pirâmide ao produto de área da base multiplicada pela altura (h) procurada:
Vp = (1/2) ⋅ 4² ⋅ h
4² ⋅ 3 = (1/2) ⋅ 4² ⋅ h
3 = (1/2) ⋅ h
h = 6 cm
Logo, a altura atingida no segundo recipiente será de 6 cm.
Exemplo 3
(Fuvest) Para medir o volume de uma pedra com formato irregular, Ana utilizou um recipiente cilíndrico de raio r = 8 cm e com água até a altura de 20 cm. Após colocar a pedra no recipiente, a altura da água subiu para 23,5 cm.
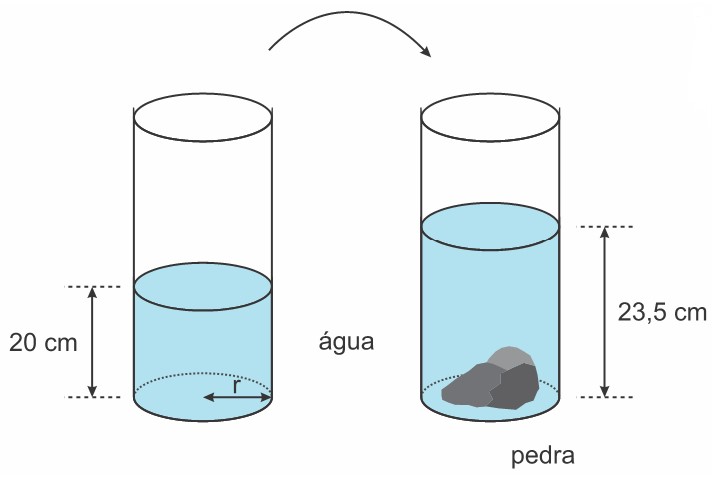
O volume da pedra é:
a) 128 π cm³
b) 224 π cm³
c) 240 π cm³
d) 282 π cm³
e) 320 π cm³
Resposta: [B]
Para descobrir o volume da pedra, basta calcular o volume de um cilindro que tem como altura (h) a diferença das alturas de água sem e com a pedra, ou seja:
23,5 − 20 = 3,5 cm
Como raio da base é r = 8 cm, temos que:
V = Ab ⋅ h = π 8² ⋅ 3,5 = 224 π cm³
Dessa forma, o volume da pedra é 224 π cm³.
☝ Leia também:
O que é Matemática básica e como ela cai no vestibular?
Números inteiros: o que são eles e como aparecem na Matemática?
Exemplo 4
(Enem) Em um terreno, deseja-se instalar uma piscina com formato de um bloco retangular de altura 1 m e base de dimensões 20 m×10 m. Nas faces laterais e no fundo desta piscina será aplicado um líquido para a impermeabilização. Esse líquido deve ser aplicado na razão de 1 L para cada 1 m2 de área a ser impermeabilizada. O fornecedor A vende cada lata de impermeabilizante de 10 L por R$ 100,00, e o B vende cada lata de 15 L por R$ 145,00.
Determine a quantidade de latas de impermeabilizante que deve ser comprada e o fornecedor a ser escolhido, de modo a se obter o menor custo.
a) Fabricante A, 26 latas.
b) Fabricante A, 46 latas.
c) Fabricante B, 17 latas.
d) Fabricante B, 18 latas.
e) Fabricante B, 31 latas.
Resposta: [A]
Para calcular a área a ser impermeabilizada, temos que descobrir a área do fundo da piscina com medidas 20 por 10, de duas laterais de medida 20 por 1 e outras duas laterais 10 por 1, todas dadas em metros. Considerando as medidas, a área em questão é dada por:
A = 20⋅10 + 2⋅20⋅1 + 2⋅10⋅1 = 260 m²
Se para cada 1m² é gasto 1L de impermeabilizante, para esta piscina serão usados 260 L. Agora comparando os fornecedores:
Fornecedor A
Nº de latas necessárias: 260÷10 = 26 latas
Valor das latas: 100⋅26 = 2600 reais
Fornecedor B
Nº de latas necessárias: 260÷15 = 17,333… → O número de latas é inteiro, por isso precisará de 18 latas.
Valor das 19 latas: 145⋅18 = 2610 reais
Comparando os valores temos que o fornecedor A será oferece o menor valor. Portanto, a compra será feita com o fornecedor A totalizando 26 latas.
🥇 Quer se preparar para o Enem e vestibulares com quem mais entende do assunto? A plataforma Aprova Total é a maior especialista no ensino digital e tem as melhores videoaulas e professores!




