Matemática básica: o que é, conteúdos e como estudar

Quem nunca se deparou com exercícios de Matemática básica e pensou: básica pra quem? Bom, se você já se fez essa pergunta, antes de falar sobre os conteúdos em específico, vamos esclarecer o que significa básica nesse caso.

Na realidade, a ideia de ser básica tem a ver com a Educação Básica do Brasil, que é dividida em Educação Infantil, Ensino Fundamental e Ensino Médio. Assim, o que chamamos de Matemática básica são os conteúdos abordados até o final do Ensino Fundamental, ou seja, até o 9º ano.

E por que estamos falando deles? É que alguns são retomados e aprofundados no Ensino Médio, construindo conceitos mais complexos ou mesmo abstratos. Então, essa Matemática básica se trata dos conteúdos vistos até o 9º ano, considerados essenciais para um bom aprendizado ao longo dos três anos de Ensino Médio - não só na Matemática, mas também em outras disciplinas, como Química, Física, Biologia, História e Geografia.

Agora que você já tem noção do que esperar, vamos aos assuntos mais importantes de Matemática básica para o Enem e os vestibulares?

Matemática básica: resumo

Para quem está procurando por uma lista mais objetiva, com os tópicos que compõem a Matemática básica, chegou o seu dia de sorte 👏 Preparamos uma lista valiosa com treze conteúdos, veja nossa seleção de tópicos:

• Sistemas de numeração
• Números Inteiros e suas operações
• Frações e suas operações
• Números decimais
• Múltiplos e divisores
• Potenciação e radiciação
• Transformação de unidades
• Expressões algébricas, produtos notáveis e fatoração
• Equações do 1º e 2º grau
• Sistema de equações
• Razão, proporção e regra de três
• Porcentagem
• Juros

Bastante coisa, né? Entre os assuntos listados, oito deles (em itálico), têm maior incidência no Enem, e aparecem de forma conectada entre si. Dividimos os temas em três tópicos. Vamos conhecê-los?

1. Números inteiros, frações suas operações e números decimais

Como no Enem as questões costumam trazer um contexto, quando se trata dos números inteiros, eles aparecem relacionados a contagem, pontuações em jogos, medidas e dívidas. Essa escolha faz sentido, já que contagem de pessoas, objetos a serem comprados, pontuação dos jogos do Brasileirão, costumam ser quantidades exatas.

Por outro lado, medidas podem ser apresentadas tanto em números inteiros como em frações. Na lista de ingredientes de receita de bolo, você terá quantidades exatas, como 3 ovos, ou quebradas, como 1 xícara e 1/2 de açúcar. Frações do tipo 3/4 também são comuns, então, se o contexto for comida ou alimentação, pode apostar que elas estarão lá.

Por último e não menos importante, quando se fala sobre dívidas, usa-se alguma unidade monetária como referência, seja ela real (R$), dólar americano (US$), euro (€), libra esterlina (£), iene japonês (¥), entre outras.

Pense na dívida mais simples possível: cinco amigos pediram um combo de pizzas por R$ 112. Enquanto um deles pagou por tudo, os demais fariam um pix no dia seguinte.

⚠️ Esta é uma situação meramente ilustrativa, cuidado com o "golpe" do depois eu faço um pix ⚠️

O valor das pizzas é um número inteiro, mas, calculando o que cada amigo está devendo, encontramos R$ 22,40, que é um número decimal. Os números decimais podem ser reescritos como frações, e vice-versa, e a melhor opção para resolver a questão varia de caso para caso.

Não existe uma regra, mas duas dicas podem iluminar suas escolhas:

• Quando a fração representa uma divisão sem muitas casas após a vírgula, e a questão traz outros números inteiros, vale a pena usar o número decimal.
  Exemplo: a fração 1/2 pode ser reescrita como 0,5.
  
• Quando um número decimal é infinito, em específico uma dízima periódica, e na questão vai precisar somar ou multiplicar esse número, vale a pena usar a fração.
  Exemplo: a dízima 0,33333333... pode ser reescrita como 1/3.

2. Potenciação e radiciação, transformações de unidades e equações de 1º e 2º grau

Quando você estuda potenciação e radiação, elas são apresentadas de forma conjunta, mas, no Enem, tendem a aparecer com outros conteúdos.

Potenciação é um conteúdo vasto, mas é comum utilizar potências de base 10 para fazer transformações em unidades de medida ou associadas à notação científica. Já radiciação aparece sempre que você precisa resolver uma equação do 2º grau, seja na fórmula de Bhaskara ou no Teorema de Pitágoras, em problemas associados à geometria.

3. Razão, proporção, regra de três e porcentagem

O combo razão, proporção e regra de três carrega o peso de ser o top 1 de Matemática no Enem há anos. A regra de três, em particular, tem potencial para se relacionar com praticamente qualquer outro conteúdo de Matemática, mas, para como recomendação de estudo, os exercícios de porcentagem são os mais comuns.

Então, antes de montar a regra de três, identificar se ela é direta ou inversamente proporcional, pode aparecer um cálculo de porcentagem sobre alguma das grandezas envolvidas. Aliás, é possível ter que usar a regra de três para descobrir o valor de uma porcentagem, em questões que abordam descontos em preços ou aumentos percentuais em gráficos.

A regra de três é versátil, serve para quebrar o galho em muitas situações, por isso é a queridinha dos estudantes. Dica: se você não está conseguindo resolver a questão de forma alguma, pergunte a si mesmo se dá para usar a regra de três ali.

Matemática básica para o Enem

Logo no início deste texto, explicamos que a Matemática básica é um conjunto de conteúdos necessários para se dar bem no Ensino Médio como um todo.

Mas, quando se trata de interdisciplinaridade, logo o Exame Nacional do Ensino Médio (Enem) vem à cabeça, né? São muitos conceitos que aparecem nas questões da prova e você ainda pode usar de repertório sociocultural.

Matemática básica e Geografia

As operações com números inteiros estão diretamente relacionadas aos 24 fusos horários que dividem o nosso planeta, no qual o meridiano de Greenwich é utilizado de referência para determinar os demais fusos.

Se você tentar ajustar o horário no seu telefone utilizando fusos horários, vai ver que existe um padrão na nomenclatura dos fusos. Há a sigla GMT, que significa Greenwich Mean Time, e um número inteiro, que representa quantas horas este fuso está adiantado ou atrasado em relação ao meridiano de Greenwich.

O Brasil, que é um país com dimensões continentais, tem mais de um fuso horário. Então, na sede no Aprova Total, em Florianópolis (Santa Cantarina), o fuso horário é GMT-3. Isso quer dizer que estamos 3 horas atrasados em relação ao meridiano de Greenwich.

Entretanto, uma pessoa que mora em Campo Grande (Mato Grosso do Sul) está no fuso horário GMT-4, ou seja, são 4 horas de atraso em relação ao meridiano de Greenwich.

Veja as cidades utilizadas de exemplo marcadas com pins no seu respectivo fuso horário:

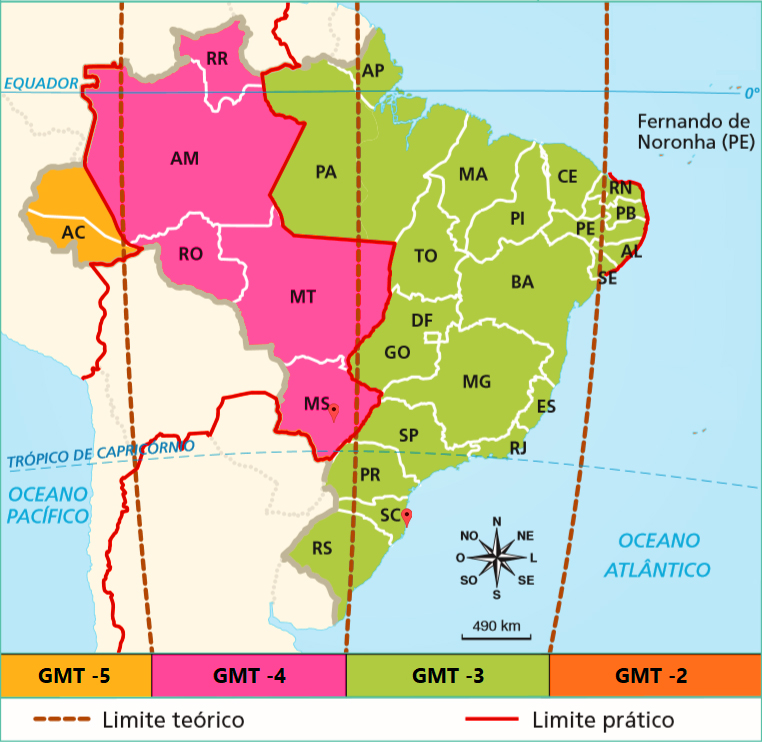
Diferenças de fusos horários

Utilizar os números inteiros para determinar a hora em diversos locais do mundo, a partir do meridiano de Greenwich, é uma aplicação simples de operações com número inteiros. Outra mais complexo é se perguntar quantas horas de diferença existem entre dois fusos horários quaisquer ao redor do planeta.

Então, acredite se quiser, a Matemática também é culpada pela frase "já é Ano Novo na Austrália!".

Exemplo: se em Brasília o fuso é GMT-3 e são dez horas da manhã, que horas são em Sidney, na Austrália, em que o fuso é GMT+10?
Para descobrir o horário de Sidney precisamos utilizar o horário de Greenwich como base. Como Brasília está 3 horas atrás de Greenwich (GMT-3), lá são 13h; e como Sidney está 10 horas à frente de Greenwich (GMT +10), basta adicionar 10 horas ao horário de Greenwich para descobrir que, em Sidney, são 23h.

No fim das contas, Sidney está 13 horas à frente do horário de Brasília, pois existem treze fusos horários entre as cidades. Para alguns cálculos é necessário considerar a linha internacional de mudança de data, mas, para essa breve contextualização, entender que, todo ano novo, a Austrália começa esse ciclo com 13 horas de antecedência em relação ao Brasil, já está de bom tamanho.

Matemática básica e História

Uma das interseções entre Matemática e História é o uso do sistema de numeração romano para subdividir o tempo, cujos símbolos são:

• I=1
• V=5
• X=10
• L=50
• C=100
• D= 500
• M=1.000

Com eles, podemos escrever datas de forma abreviada. É importante lembrar que o sistema romano é posicional, ou seja, a ordem dos símbolos pode alterar o valor numérico. Por isso, os números IV e VI são escritos com os mesmos símbolos, mas IV representa 4 e VI significa 6.

Exemplo: fazendo apenas uma mudança de símbolos, no século XIV estávamos na Idade Média, por outro lado, no século XVI já vivíamos na Idade Moderna.
Pode parecer inofensivo, no entanto, uma leitura equivocada de números romanos faria você confundir esses períodos históricos.

Outra confusão comum é sobre o período que cada século representa. Mas a grande sacada na leitura é saber que o século termina no valor dos números em romanos:

• Século XIV: o número XIV em romanos representa 14; portanto, esse século termina em 1400. Assim, como um século representa 100 anos, ele começa em 1301.
  
• Século XVI: o número XVI em romanos representa 16; portanto, esse século termina em 1600. Assim, como um século representa 100 anos, ele começa no ano 1501.

Viu só? A Matemática básica ajuda você a determinar datas, especialmente quando os séculos estiverem envolvidos.

Matemática básica e Ciências exatas e da natureza

Dentro desta grande área que é Ciências exatas e da natureza, cada disciplinas certamente merece um texto detalhado, pois são assuntos alta incidência no Enem - mas, vamos por etapas. Aqui, vamos apresentar informações menos aprofundadas, mas que certamente vão aguçar a sua curiosidade.

Química

Especificamente na estequiometria, a regra de três é essencial. A partir dela calcula-se mol, massa, rendimento, pureza e muito mais.

Exemplo: para determinar o número de mols de NaOH que vai reagir com 3 mols de ácido sulfúrico, utilizando a equação química já balanceada 2 NaOH + H₂SO₄ → Na₂SO₄ + 2 H₂O, podemos utilizar regra de três simples.
Como para cada mol de H₂SO₄ reagem 2 mols de NaOH, para encontrar quantos mols de NaOH vão reagir a 3 mols de H₂SO₄, montamos uma regra de três:
1 mols de H₂SO₄ ———— 2 mols de NaOH
3 mols de H₂SO₄ ———— x mols de NaOH
x = 6 mols de NaOH

Então, usando a regra de três, descobrimos que, para 3 mols de H₂SO₄, reagem 6 mols de NaOH.

Biologia

Em genética, chovem percentuais de todos os lados. Nesse caso, o conteúdo de porcentagem está atrelado aos de probabilidade e análise combinatória.

Exemplo: o fator Rh do sangue humano pode ser relacionado a um par de genes, em que R representa o gene dominante, o fator Rh positivo; e r representa o gene recessivo, o fator Rh negativo.

Imagine a seguinte situação: um pai Rr e uma mãe rr gostariam de saber sobre o possível fator Rh dos filhos. Veja as combinações:

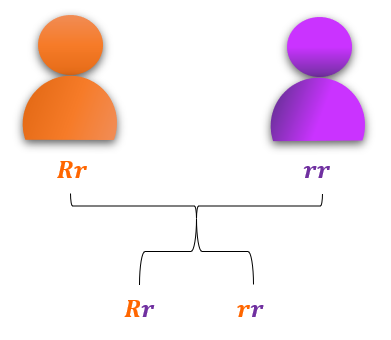
Então, são 50% de chance de ter fator Rh positivo e 50% de chance de ser negativo, porque existem apenas duas combinações de genes.

Algumas combinações podem dar mais trabalho: se ambos os pais são Rr, passamos a ter quatro combinações de genes e a chance de ter fator Rh negativo cai para 25%. Mas se qualquer um deles for RR, a chance cai para 0%, ou seja, não há possibilidade de ter um filho com fator Rh negativo.

Quem deseja se aprofundar em genética (ei, vestibulandos de Medicina!) e tem interesse no assunto, dominar os cálculos de porcentagem trazer uma vantagem imensa.

Matemática básica do zero

Os conteúdos de Matemática básica são úteis muito além da disciplina. Por isso, é importante que você se dedique a eles desde o começo dos seus estudos.

Não adianta ir direto nas geometrias, funções e análise combinatória, sem os conhecimentos de Matemática básica para o Enem e outros vestibulares. Além de gastar seu tempo estudando Matemática do jeito errado, você ainda pode acabar se frustrando e criando bloqueios com o tema.

Por isso, invista no arroz com feijão da Matemática - ela mesma, a Matemática básica. Com esse conhecimento absorvido, os outros vão fluir melhor.

🥇 Quer preparação máxima para ter alto rendimento no Enem e ingressar no curso dos seus sonhos? 
Então conheça a plataforma do Aprova Total!