Porcentagem: o que é, como calcular e exercícios resolvidos

Este post é dedicado à porcentagem, que, além de ser uma das queridinha dos estudos de Matemática, aparece em situações relacionadas a diversas áreas, como estatística, genética, demografia, economia, finanças e tantas outras. Mas, afinal, por que a porcentagem é comum a contextos tão distintos?

Intuitivamente, utiliza-se o conceito de porcentagem quando é necessário expressar proporções ou partes em relação a um todo.

Um dos exemplos mais comuns do uso da porcentagem no dia a dia é a bateria do celular. Todo mundo fica feliz quando ela está cheia, entre os 90% e 100%. Complicado mesmo é sair para o rolê pedindo socorro, com menos de 20%, pois existe o risco de não sobrar nem para pedir o Uber.

É interessante saber, porém, que as baterias de telefone têm capacidades diferentes de armazenar energia, dependendo do modelo de smartphone. Isso quer dizer que 50% da bateria pode ser 5 horas para o seu celular e, para o da sua mãe, apenas 3 horas.

A porcentagem, então, vai resultar em valores diferentes, dependendo do total de armazenamento de energia de cada smartphone.

Guarde esses termos para outro momento da leitura: partes do todo e partes de um total.

Agora, vamos conhecer mais sobre porcentagem, do básico ao conceito matemático formal e como calculá-la nas mais diversas situações.

Qual o conceito de porcentagem e seu símbolo?

De forma quase literal, a palavra porcentagem significa por cento, ou seja, por cada cento.

Então, quando você vê o símbolo %, significa que a quantidade em questão está sendo expressa em relação a 100 unidades. Há quem defina mais formalmente o símbolo como unidade de medida, expressando proporção ou parte de um todo em relação a 100.

Um detalhe que vale a pena destacar é que a palavra porcentagem tem alguns sinônimos que aparecem dependendo do contexto. Então, se você ler percentual, percentagem, percentil, taxa e, em conceitos específicos de finanças, alíquota, o assunto também é porcentagem.

Entendê-la como a relação de uma certa quantidade a 100 é mais fácil quando a escrevemos em forma de fração. Assim, quando se diz 30% significa que são 30 partes de 100, ou 30/100, sendo essa a forma fracionária de 30%.

Como nem sempre é prático utilizar frações, em alguns casos, é possível usar nos cálculos a divisão 30/100 e o seu resultado, que é 0,3. O valor 0,3 é a forma decimal de 30% e a escrita acompanhada do símbolo % é a forma percentual.

Todas as possíveis formas de representar porcentagem são equivalentes, por isso você sempre vai encontrar o mesmo resultado. Veja:

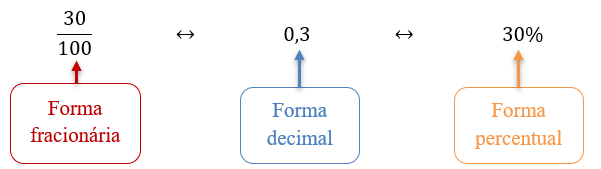
Agora que você sabe como escrever porcentagens, vamos ao próximo passo: fazer cálculos!

Os percentuais estão muito presentes no comércio, nos bancos, nos mercados, principalmente quando há aumento ou redução de preços.

Como calcular a porcentagem de um valor?

Para calcular a porcentagem de algum valor, podemos fazer de dois tipos de cálculo, utilizando a forma decimal e ou a fracionária.

Imagine que quatro turmas de Terceirão se juntaram, totalizando 120 estudantes, para organizar uma excursão no final do ano. Os pacotes disponíveis na agência de viagem tinham como destino Florianópolis (SC), Porto Seguro (BA) e Bonito (MS).

Considerando a quantidade de estudantes, a agência garantiu que com 40% escolhendo qualquer um dos três destinos, a viagem era viável.

Para descobrir o número necessário de alunos para fechar um pacote, precisamos multiplicar o total de estudantes pela porcentagem solicitada.

Então, vamos utilizar a forma fracionária para encontrar 40% de 120:

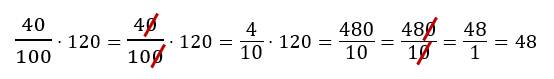
Assim, o mínimo para fechar o pacote de viagem são 48 estudantes. Com essa informação, eles se dividiram em dois grupos: o primeiro com 72 pessoas que iriam para Porto Seguro; e o segundo com 48 que escolheram Florianópolis.

Como o primeiro grupo tinha reunido muitos estudantes além do que a agência propôs, eles queriam negociar um desconto de 5% para cada viajante. Essa viagem custaria R$ 5.200, mas a agência aceitou a proposta, desde que o valor fosse parcelado em, no máximo, 3 vezes.

Dessa forma, o desconto oferecido para cada estudante foi de:

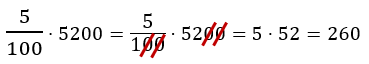
Ou seja, 5% seriam exatamente R$ 260. Graças a essa negociação, a viagem passou de R$ 5.200 para R$ 4.940, sendo que, para chegar a esse valor, foi preciso subtrair o desconto calculado, de 5%, do valor inicial, de R$ 5.200.

Com esse exemplo, você pode ter achado pouco o valor de desconto, mas, para a agência de viagem, esses 5% de desconto oferecidos para as 72 pessoas somam R$ 18.720.

De forma genérica, sempre que quiser calcular 𝑥% de um valor 𝑝 qualquer, basta calcular a seguinte multiplicação:

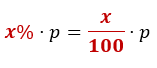
Descontos percentuais

No exemplo anterior, fizemos duas contas separadas: primeiro, calculamos o desconto e, depois, o novo valor da viagem, subtraindo o do desconto.

De forma genérica, com um valor 𝑝 qualquer e 𝑥% de desconto, o valor final é dado pela subtração do desconto ao valor de 𝑝, ou seja:

Valor final: 𝑝 - 𝑥% ⋅ 𝑝

É possível fazer apenas um cálculo só ao invés de dividi-lo em duas etapas para descobri o valor final após um desconto de 𝑥%.

Vamos retornar à viagem que custava R$ 5.200 e recebeu 5% de desconto. Para essas situações, utilizamos a forma decimal e, no caso dos descontos, subtraímos de 1 o percentual dado e multiplicamos pelo valor da viagem.

Transformando 5% para sua forma decimal encontramos 0,05 e subtraindo esse valor de 1, chegamos em 0,95. Esse valor deve ser multiplicado por R$ 5.200, assim encontraremos o valor da viagem já com o desconto:

5.200 ⋅ 0,95 = 4.940

De forma genérica, dado um valor 𝑝 qualquer e 𝑥% de desconto, o cálculo direto para o valor final é dado por:

Valor final: 𝑝 ⋅ ( 1 - porcentagem em decimal)

Aumentos percentuais

No caso dos aumentos, há uma lógica parecida para calcular por duas etapas ou de forma direta.

De forma genérica, com um valor 𝑝 qualquer e 𝑥% de aumento, o valor final é dado pela adição do aumento ao valor de 𝑝, ou seja:

Valor final: 𝑝 + 𝑥% ⋅ 𝑝

Se a viagem que custava R$ 5.200 oferecesse a opção de pagar em mais que 3 vezes, porém com um acréscimo de 5%, teríamos um aumento de R$ 260 e a viagem passaria a custar R$ 5.460.

Transformando 5% para sua forma decimal, encontramos 0,05 e adicionando esse valor de 1, chegamos em 1,05. Esse valor deve ser multiplicado pelo R$ 5.200, assim encontraremos o valor da viagem já com o aumento:

5.200 ⋅ 1,05 = 5.460

De forma genérica, com um valor 𝑝 qualquer e 𝑥% de aumento, o cálculo direto para o valor final é dado por:

Valor final: 𝑝 ⋅ ( 1 + porcentagem em decimal)

Leia também:

O que estudar em Química para o Enem 2023?

Temas de Biologia que você deve priorizar para o Enem 2023

Física no Enem: quais assuntos devem cair em 2023?

Dicas e macetes para cálculo de porcentagem

Em alguns exercícios, a solução é aceitar que dói menos. Ou seja, isso quer dizer que os cálculos de porcentagem ficam enormes utilizando a forma fracionária ou resultam em muitas casas após a vírgula ao usar a forma decimal.

Então, se você chegou até esse post em busca de uns macetinhos, selecionamos dois casos especiais:

No último exemplo a vírgula não está escrita de forma explícita. Como 60 é um número inteiro, escrevê-lo na forma decimal seria adicionar um vírgula e um zero a direita: 60,0. Após escrever a vírgula, basta descolar a vírgula e obteremos 6,00.

Quanto é 50% de um valor?

Para calcular 50% de qualquer valor, basta dividir por 2.

Isso mesmo, 50% é a metade de um valor, simples assim. Pode parecer ✨mágica✨, mas fica mais claro se você utilizar a porcentagem em sua forma fracionária:

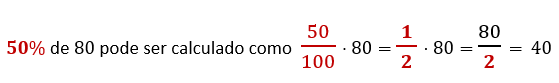
Ou seja, simplificando a fração da porcentagem antes de realizar a multiplicação, basta apenas dividir o valor final por 2:

• se foi anunciado um aumento de 50% na passagem aérea de R$ 150, foi um aumento de R$ 75
• se foram encomendados 400 salgadinhos de festa e 50% são vegetarianos, são 200 salgadinhos de festa disponíveis para os vegetarianos
• se uma promoção de curso de pintura oferece 50% de desconto e o curso custava R$ 320, o desconto é de R$ 160

Como a porcentagem pode cair no Enem?

No Exame Nacional do Ensino Médio (Enem), a porcentagem é um daqueles conteúdos interdisciplinares que pode cair em Física, Química, Biologia e até Geografia. Agora, veja bem, pode cair nas outras disciplinas, mas na Matemática é certeza que vai cair.

Tão certo quanto 2+ 2 são 4, é o conteúdo de porcentagem na prova do Enem, pois ele está presente na matemática básica, que domina a incidência da prova.

Podemos classificar a maioria dos problemas de porcentagem em três tipos: cálculo direto, cálculo envolvendo gráficos ou tabelas e cálculos sucessivos envolvendo comparação.

• Os cálculos diretos aparecem em questões de texto corrido e, em geral, é necessário encontrar uma porcentagem específica, o aumento ou decréscimo a partir de um valor;
  
• Nos cálculos envolvendo gráficos ou tabelas, a diferença é que os valores estão justamente nos gráficos ou nas tabelas, assim, você precisará escolher quais deles usar e como;
  
• As questões de cálculos sucessivos envolvendo comparação são as clássicas do Enem. Nelas, você terá que fazer todas as conta, interpretar e comparar os resultados para chegar a uma conclusão.

Para exemplificar essas classificações, veja abaixo um exercício de cada caso:

Exercício 1: cálculo direto

(Enem) Em janeiro de 2013, foram declaradas 1.794.272 admissões e 1.765.372 desligamentos no Brasil, ou seja, foram criadas 28.900 vagas de emprego, segundo dados do Cadastro Geral de Empregados e Desempregados (Caged), divulgados pelo Ministério do Trabalho e Emprego (MTE). Segundo o Caged, o número de vagas criadas em janeiro de 2013 sofreu uma queda de 75%, quando comparado com o mesmo período de 2012.

Disponível em: http://portal.mte.gov.br. Acesso em: 23 fev. 2013 (adaptado).

De acordo com as informações dadas, o número de vagas criadas em janeiro de 2012 foi

a) 16.514.
b) 86.700.
c) 115.600.
d) 441.343.
e) 448.568.

Resposta: [C]
Com base nas informações apresentadas no enunciado, sabemos que o número de vagas criadas em janeiro de 2013 sofreu uma queda de 75%, quando comparado com o mesmo período de 2012.

Para fazer o cálculo de forma direta, lembre de que 75% de queda em relação a 2012 é o mesmo que multiplicar o número de vagas criadas em 2012 por 1 - 0,75 = 0,25. Chame o número de vagas criadas em 2012 de 𝑥.

Assim, como sabemos que o número de 2013 foi 28.900, temos a seguinte igualdade: 𝑥 ⋅ 0,25 = 28.900
Isolando o 𝑥, temos que: 𝑥 =  28.900/0,25 =115.600 

Exercício 2: cálculo envolvendo gráfico

(Enem) O abandono escolar no Ensino Médio é um dos principais problemas da educação no Brasil. Reduzir as taxas de abandono tem sido uma tarefa que exige persistência e ações continuadas dos organismos responsáveis pela educação no país.

O gráfico apresentado a seguir mostra as taxas percentuais de abandono no ensino médio, para todo o país, no período de 2007 a 2010, em que se percebe uma queda a partir de 2008. Com o objetivo de reduzir de forma mais acentuada a evasão escolar são investidos mais recursos e intensificadas as ações, para se chegar a uma taxa em torno de 5,2% ao final do ano de 2013.

Qual a taxa de redução anual que deve ser obtida para que se chegue ao patamar desejado para o final de 2013? Considere (0,8)³ ≅ 0,51. 

a) 10%
b) 20% 
c) 41% 
d) 49%
e) 51%  

Resposta: [B]
Chame de i a taxa de redução anual que estamos procurando.
Em 2010, o percentual de abandono foi de 10,3%, sendo que o patamar desejado para 2013 é de 5,2%. 
Como se trata de uma redução ao longo de três anos, para calcular o valor de i, basta multiplicar o percentual 10,3 por (1 - i)³ e igualar a 5,2.
Segue que:
10,3 ⋅ (1 - i)³ = 5,2 
         (1 - i)³ = 5,2/10,3
          (1 - i)³ ≅ 0,51      ⟶      Substituímos 0,51 por (0,8)³
          (1 - i)³ ≅ (0,8)³
             1 - i ≅ 0,8
          1 - 0,8 ≅ i
               0,2 ≅ i
Se a taxa encontrada foi 0,2, para encontrar o valor em porcentagem basta multiplicar por 100 e adicionar o símbolo %. Dessa forma, após calcular a multiplicação obtemos 20%.

Exercício 3: cálculos sucessivos envolvendo comparação

(Enem) Em uma loja, o preço promocional de uma geladeira é de R$ 1.000,00 para pagamento somente em dinheiro. Seu preço normal, fora da promoção, é 10% maior. Para pagamento feito com o cartão de crédito da loja, é dado um desconto de 2% sobre o preço normal.

Uma cliente decidiu comprar essa geladeira, optando pelo pagamento com o cartão de crédito da loja. Ela calculou que o valor a ser pago seria o preço promocional acrescido de 8%. Ao ser informada pela loja do valor a pagar, segundo sua opção, percebeu uma diferença entre seu cálculo e o valor que lhe foi apresentado.

O valor apresentado pela loja, comparado ao valor calculado pela cliente, foi 

a) R$ 2,00 menor.
b) R$ 100,00 menor. 
c) R$ 200,00 menor.  
d) R$ 42,00 maior.  
e) R$ 80,00 maior.

Resposta: [A]
O preço da geladeira fora da promoção é 1,1 ⋅ 1000 = R$ 1.100. Por outro lado, o preço da geladeira no cartão de crédito é 0,98 ⋅ 1100 = R$ 1.078.

No cartão de crédito, o preço da geladeira, segundo o cálculo da cliente, é 1,08 ⋅ 1000 = R$ 1.080. Calculando a diferença entre o preço da loja e o cálculo da cliente, encontramos 1078 − 1080 = - 2. Portanto, o valor apresentado pela loja, comparado ao valor calculado pela cliente foi R$ 2 menor.

Resumo

Depois desta mega revisão de porcentagens, exemplos do dia a dia, macetinhos para questões e exercícios do Enem, vamos retomar os tópicos mais importantes para fechar com chave de ouro, ok?

Conceito de porcentagem

• Definição intuitiva: porcentagem quer dizer "por cento", ou seja, quando você vê o símbolo %, significa que a quantidade em questão está sendo expressa em relação a 100 unidades.

• Definição de cálculo percentual: o percentual de um determinado valor resulta da multiplicação de uma taxa percentual pelo valor em questão. 

Exemplo: 20% de 80 é 16, pois 20% ⋅ 80 = (20/100) ⋅ 80 = 1600/100 = 16 

Aumentos e descontos

Em problemas de aumento e desconto, para simplificar cálculos, convém transformar o percentual em sua forma decimal. Para fazer essa mudança, divida o valor antes do símbolo de porcentagem por 100 e descarte o símbolo %.

Exemplo: 20% é 0,2, pois 20% = (20/100) = 0,2 

Quando quisermos saber o valor final de um produto, após aplicar um aumento de 40%, faça apenas uma multiplicação, somando os 40% da seguinte forma:

•  Aumento: 1 + taxa de aumento = 1 + 0,4 = 1,4

Então, para descobrir qual o valor final após um aumento de 40%, basta multiplicar por 1,4 o valor do produto.

Com descontos, há um lógica parecida. Para saber o valor final do produto depois de aplicar um desconto de 40%, também fazendo apenas uma multiplicação, subtraia os 40% da seguinte forma:

•  Desconto: 1 - taxa de aumento = 1 - 0,4  = 0,6

Então, para descobrir qual o valor final após um desconto de 40%, basta multiplicar por 0,6 o valor do produto.

Sempre é possível montar um regra de 3 para descobrir o percentual de um determinado valor.
Para isso, basta montar a regra de 3 em que o valor de referência esteja para 100% e considerar que x está para o percentual que você quer descobrir.

🥇 Quer se preparar para o Enem e vestibulares com quem mais entende do assunto? A plataforma Aprova Total é a maior especialista no ensino digital e tem as melhores videoaulas e professores!