Geometria plana: principais conceitos, fórmulas e exercícios
Se você tem medo dessa área da Matemática, preparamos um guia com tudo explicado em detalhes - para não passar mais sufoco na hora de resolver as questões

Acessibilidade
Bem-vindos ao maravilhoso mundo da geometria plana, onde triângulos, quadrados e círculos se reúnem para fazer o que fazem de melhor: confundir estudantes e, ocasionalmente, parecer mais complicados do que deveriam! 👀
Você já se perguntou por que um triângulo tem três lados e não quatro ou cinco? Ou por que um círculo é a forma perfeita para um disco voador?

Prepare-se para uma jornada cheia de ângulos estranhos, linhas retas e outras coisas mais, enquanto desvendamos os mistérios da geometria plana. Mas, não se preocupe, mesmo que a Matemática seja o seu "triângulo amoroso" ou o seu "ponto fraco," estamos aqui para simplificar e, com um pouco de diversão, transformar essas formas em suas velhas amigas. Então vamos à geometria plana?
NAVEGUE PELOS CONTEÚDOS
Conceitos básicos de geometria plana
Para iniciar o estudo da geometria plana, é essencial estabelecer os seus elementos fundamentais. Os conceitos, como ponto, reta e plano, não podem ser completamente definidos de forma independente. Qualquer tentativa de definição acaba sendo circular, ou depende de outros conceitos indefinidos.
Na obra Os elementos, um tratado matemático e geométrico escrito pelo grego Euclides, em Alexandria, por volta de 300 a.C, a linha é descrita como um comprimento sem largura. Porém, os conceitos de comprimento e largura permanecem indefinidos, e frequentemente se classificam como conceitos primitivos.
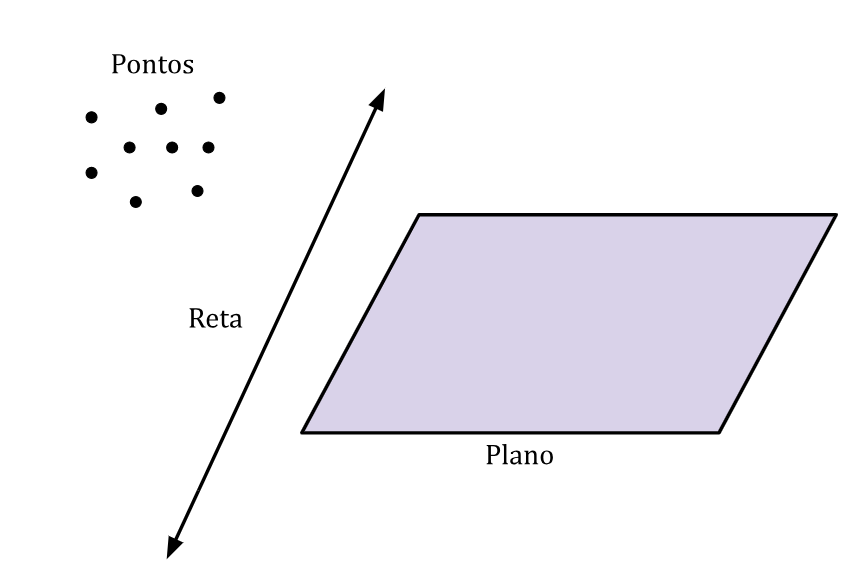
Pontos
Um ponto, no sentido matemático, é uma abstração de nosso senso comum de indivisibilidade. É um objeto que não pode ser decomposto em outros menores e no qual não existe qualquer extensão, isto é, não podemos “nos deslocar” dentro de um ponto.
Dizemos que um ponto é um objeto de dimensão zero, ou ainda que um ponto não possui graus de liberdade. Geralmente o denotamos por letras maiúsculas:
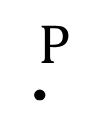
Reta, semirreta e segmento de reta
Agora, falando sobre objetos de uma dimensão temos as retas, as semirretas e os segmentos de retas, um conjunto de pontos com algumas características específicas.
Reta: figura geométrica unidimensional que se estende indefinidamente em ambas as direções. Uma reta possui sequência infinita de pontos alinhados e, geralmente, a denotamos por letras minúsculas:
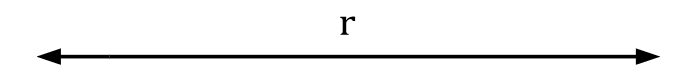
📢 A seta representa uma extensão infinita na direção a qual ela indica.
Semirreta: conceito geométrico que se assemelha a uma reta, mas tem ponto de partida específico chamado de origem e continua indefinidamente em uma única direção.
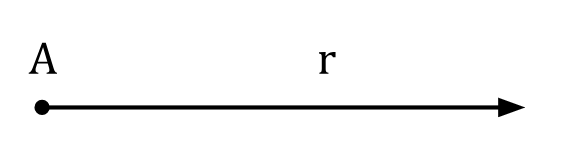
Segmento de reta: um segmento de reta é uma parte limitada de uma reta que consiste em dois pontos extremos e em todos os pontos que estão entre esses extremos.

Cada um destes objetos apresentados possui uma notação específica quando se trata dos seus pontos

Planos
Os planos são uma superfície bidimensional que se estende infinitamente em todas as direções. Um plano é completamente plano, não tem espessura e é composto por uma infinidade de pontos que estão alinhados em uma única superfície. Não importa em que direção você se mova dentro de um plano, você permanecerá dentro desse plano. Geralmente o denotamos por uma letra grega minúscula:

Um plano é descrito como sendo infinito em extensão nas direções horizontal e vertical, mas ainda assim é uma superfície plana, sem profundidade. Pode ser representado graficamente como uma folha de papel ou um quadro bidimensional, mas, na realidade, um plano não tem bordas ou limites.
Ângulos
De forma geral, definimos ângulos por semirretas concorrentes e de mesma origem. Em geometria plana, associamos um valor numérico, medido em graus, para indicar quão "aberto" estão esses dois segmentos. Esse valor também indica a orientação de abertura. Essas linhas ou segmentos são chamados de lados do ângulo, e o ponto comum é chamado de vértice do ângulo.
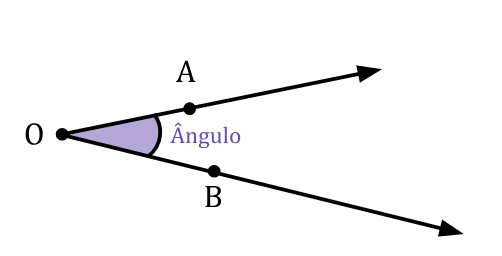
E como podemos referenciar um ângulo específico? Há duas formas de realizarmos esse processo.
A primeira é utilizar os pontos que definem os segmentos: observe a imagem acima, temos duas semirretas definidas pelos pontos A, O e B, então chamaremos esse ângulo de BÔA (usaremos sempre o sentido anti-horário).
A segunda forma é associar ao ângulo, uma letra grega minúscula, como α ou β (alpha ou beta). A medida de um ângulo geralmente é expressa em graus (°). No entanto, os ângulos também podem ser medidos em radianos, grados e outros sistemas de medida.
Existem vários tipos de ângulos com base em suas medidas:
Ângulo agudo: tem medida menor que 90 graus.
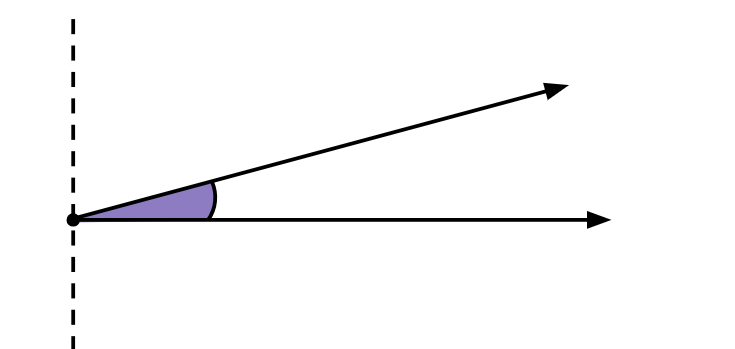
Ângulo reto: tem medida exatamente igual a 90 graus. É uma interseção de duas linhas que forma um canto de 90 graus, como o canto de uma folha de papel.

Ângulo obtuso: tem medida entre 90 e 180 graus.
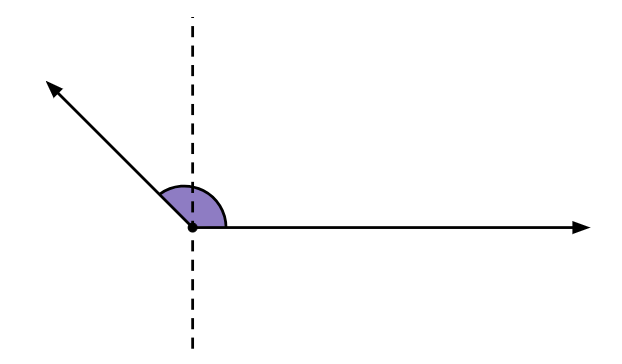
Ângulo raso: tem medida exatamente igual a 180 graus. Nesse caso, os lados são uma extensão direta um do outro.
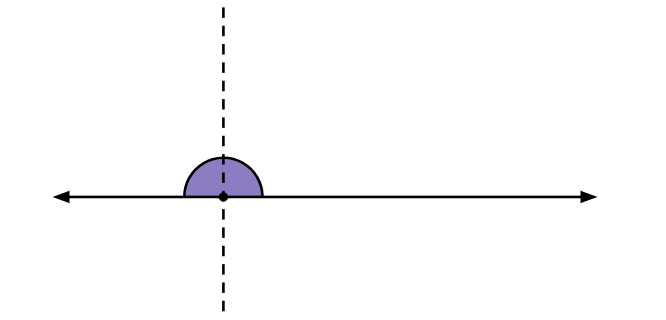
Note que no ângulo raso as semirretas que o delimitam formam uma reta.
Área
Área é uma medida que descreve a extensão ou a superfície de uma figura plana ou tridimensional. Sua quantidade nos diz quanto espaço uma forma geométrica ocupa em um plano ou no espaço. O cálculo da área depende do tipo de figura ou forma que estamos medindo.
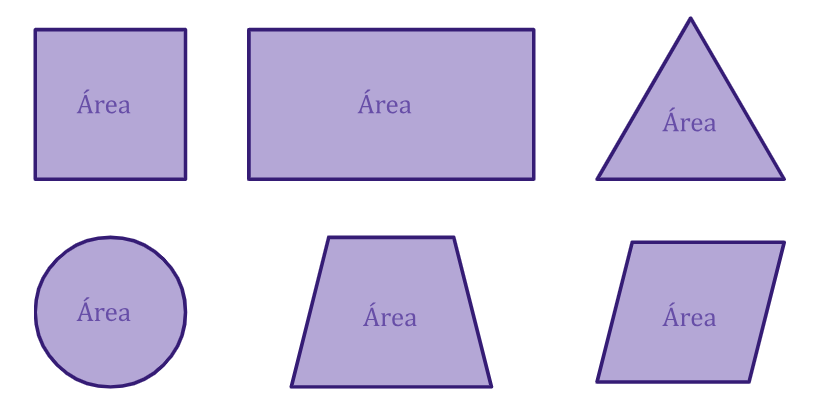
A medida da área vai depender das medidas utilizadas na figura. Por exemplo, um quadrado com lado em centímetros vai ter sua área em cm2 .
👉 Leia também:
Geometria espacial: tudo o que você precisa saber
Regra de três: simples, composta, como calcular e exercícios
Perímetros
O perímetro é uma medida que descreve o comprimento total de uma figura ou forma, que geralmente se refere à soma das medidas dos lados de uma figura geométrica. O cálculo do perímetro depende do tipo de figura que estamos considerando.
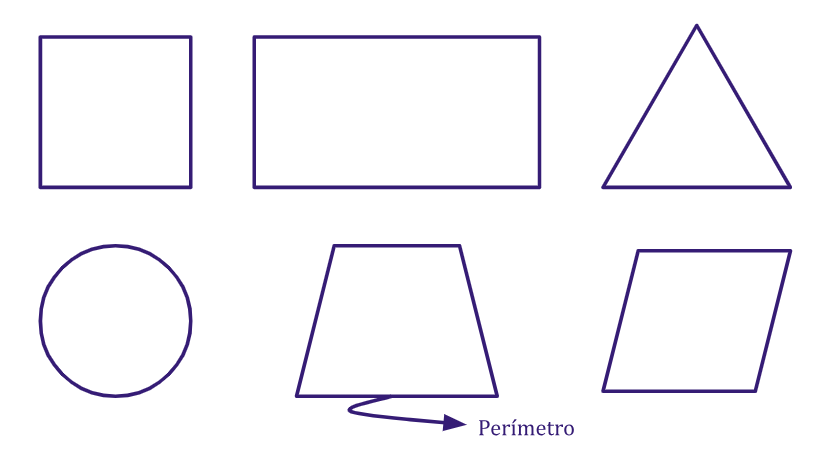

Conheça as principais figuras planas, conceitos e fórmulas
Na geometria plana, encontramos um fascinante mundo de formas e estruturas que desempenham papel fundamental em nossa compreensão do espaço e das relações entre diferentes elementos geométricos.
Triângulo
Um triângulo é uma figura geométrica plana composta por três lados e três ângulos. Os triângulos são uma das formas mais simples e fundamentais da geometria plana, além de estarem presentes em diversos ramos da Matemática e outras ciências.

Classificação de triângulos
- Triângulo equilátero: todos os lados desse triângulo possuem comprimento igual e ângulos com a mesma medida.
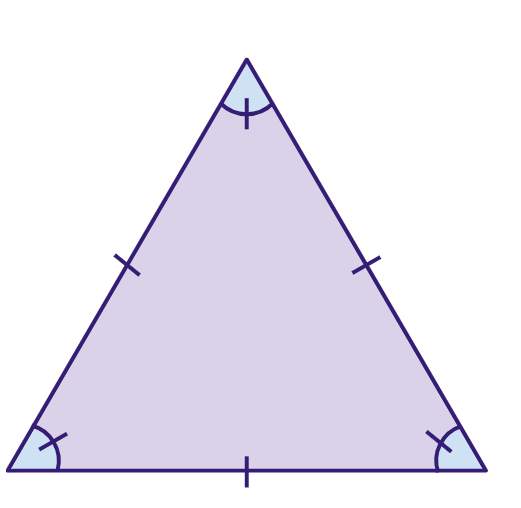
- Triângulo isósceles: possui dois lados de comprimento iguais e ângulos da base com mesma medida.
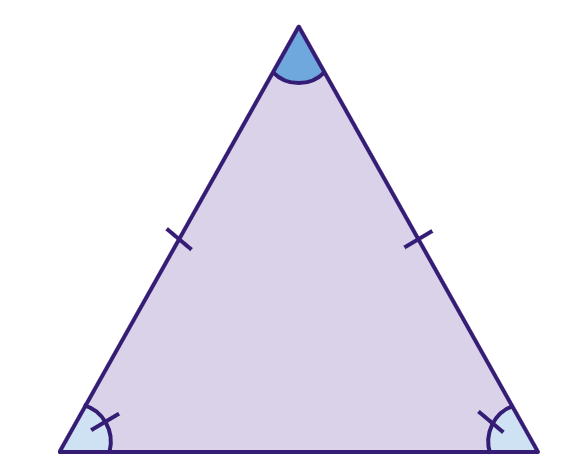
- Triângulo escaleno: um triângulo em que todos os lados têm comprimentos diferentes.
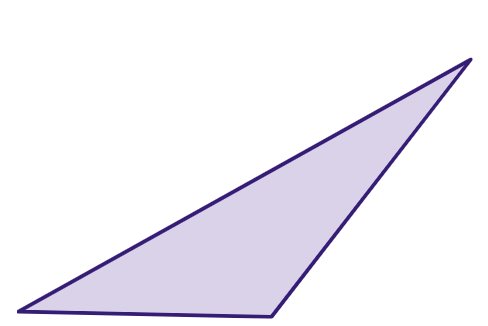
Classificação de triângulos por ângulos
- Triângulo retângulo: um triângulo que tem um ângulo reto (90 graus).
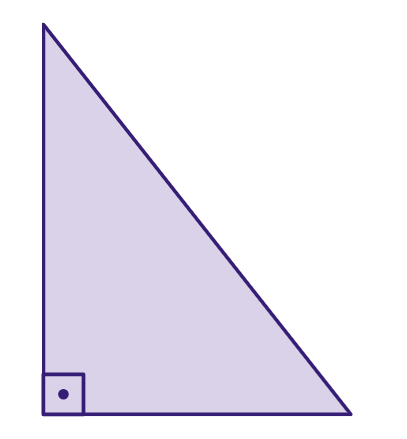
- Triângulo acutângulo: todos os ângulos são agudos (menos de 90 graus).
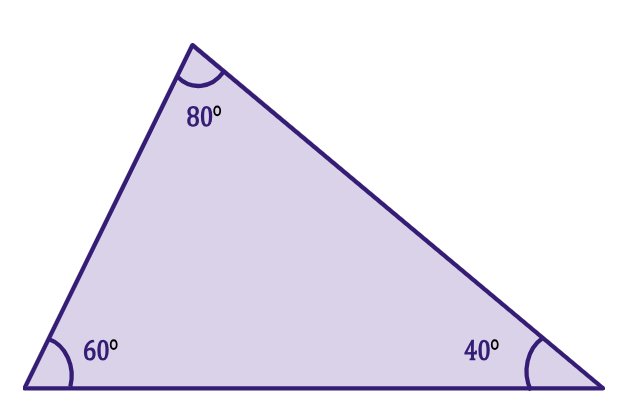
- Triângulo obtusângulo: possui um ângulo obtuso (mais de 90 graus).
Propriedades importantes do triângulo
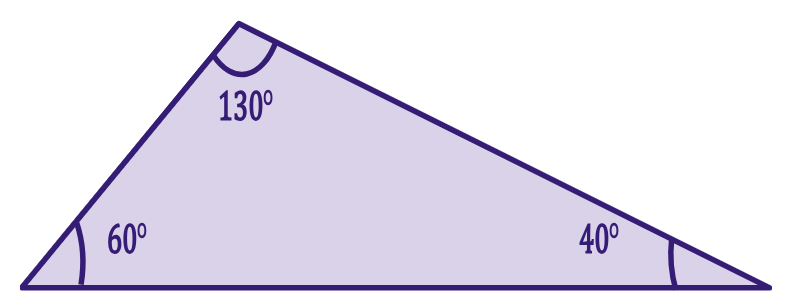
- A soma dos ângulos internos de um triângulo sempre totaliza 180 graus.
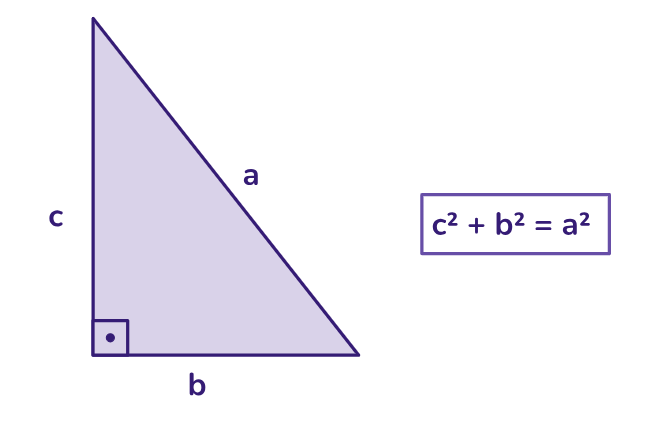
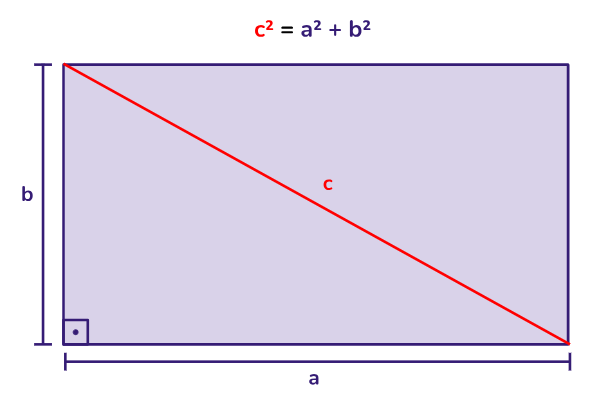
- O teorema de Pitágoras é aplicável a triângulos retângulos e estabelece a relação entre os lados de um triângulo retângulo: c2 + b2 = a2, onde "c" e "b" são os comprimentos dos catetos e "a" é o comprimento da hipotenusa.
- A desigualdade triangular afirma que a soma de quaisquer dois lados de um triângulo deve ser maior que o terceiro lado.
Área do triângulo
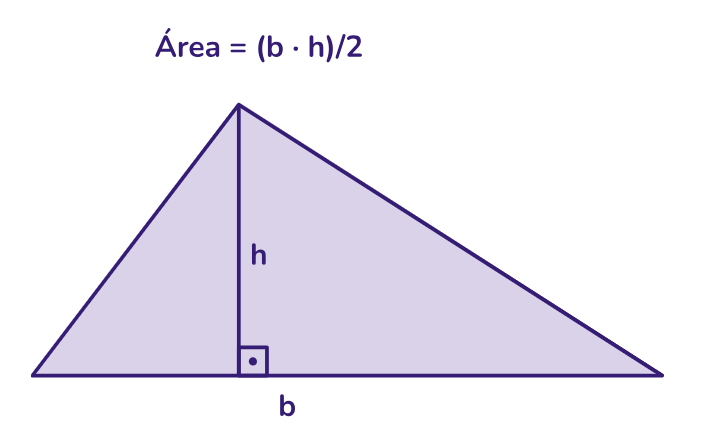
A fórmula básica para calcular a área de um triângulo é (base x altura) / 2, onde a base é o comprimento de um dos lados do triângulo e a altura é a distância perpendicular entre a base e o vértice oposto.
Quadrado
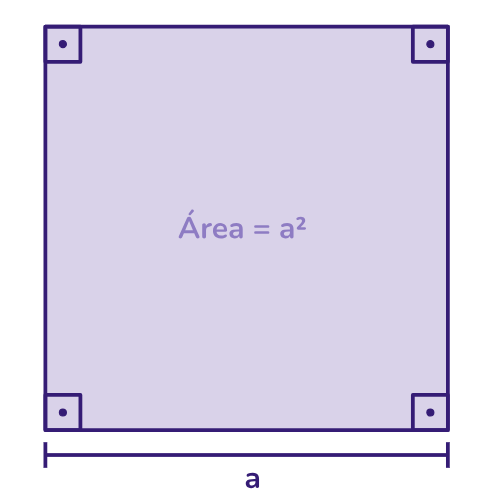
O quadrado é uma figura geométrica bidimensional que possui quatro lados de igual comprimento e quatro ângulos retos (90 graus). Isso significa que todos os lados do quadrado têm o mesmo comprimento e que seus ângulos internos medem exatamente 90 graus.

Área do quadrado: pode ser calculada multiplicando o comprimento de um de seus lados pelo próprio lado, sendo (a) o lado do quadrado temos que sua área é a2.
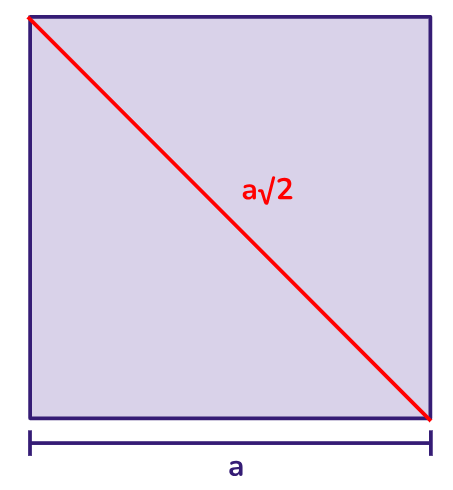
Diagonal do quadrado: um quadrado possui duas diagonais que conectam os vértices opostos. As diagonais de um quadrado também têm o mesmo comprimento e dividem o quadrado em dois triângulos retângulos idênticos. Seu comprimento é sempre a multiplicação do seu lado por √2.
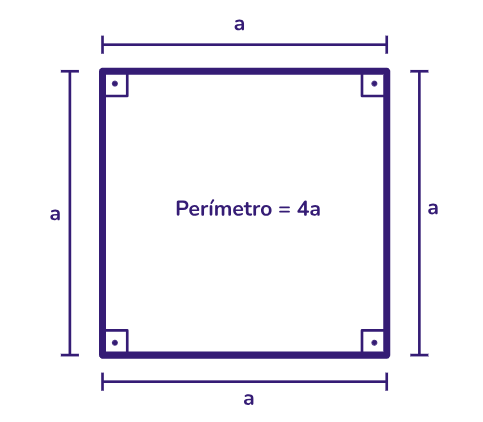
Perímetro do quadrado: o perímetro de um quadrado é a soma dos comprimentos de seus quatro lados: Perímetro = 4 · a.
Retângulo
Um retângulo é uma figura geométrica bidimensional que possui quatro lados e quatro ângulos retos (de 90 graus). Essa característica o torna um tipo específico de quadrilátero.

Propriedades fundamentais dos retângulos:
- os lados opostos de um retângulo têm o mesmo comprimento, o que significa que os lados adjacentes são iguais em pares.
- os diagonais de um retângulo têm o mesmo comprimento e se cruzam no centro do retângulo em ângulos retos.
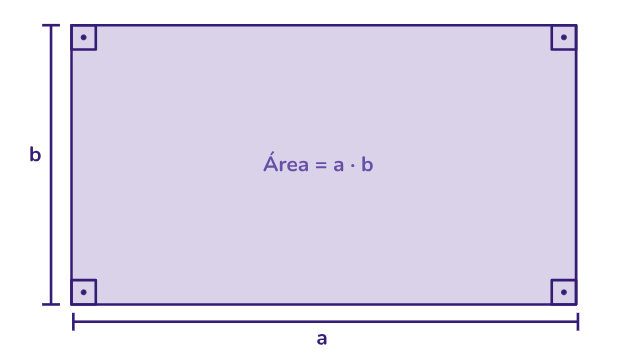
Área do retângulo: a área de um retângulo pode ser calculada multiplicando seu comprimento e largura: Área = Comprimento x Largura
Perímetro do retângulo: o perímetro de um retângulo é a soma dos comprimentos de todos os seus lados: Perímetro = 2 x (comprimento + largura).
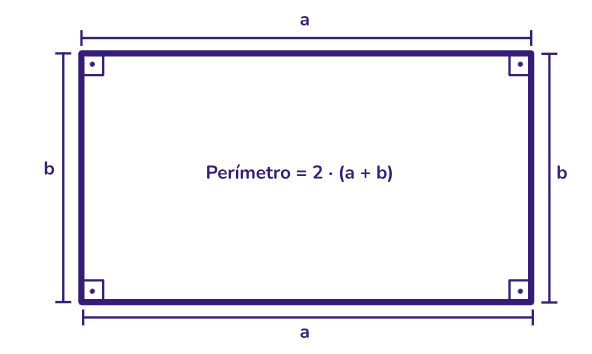
🚨 Todo quadrado é um retângulo, porém nem todo retângulo é um quadrado. 🚨
Círculo
Um círculo é uma figura geométrica bidimensional que consiste em todos os pontos que estão a uma distância constante (raio) de um ponto central (centro). Essa distância é chamada de raio e é igual em todas as direções.
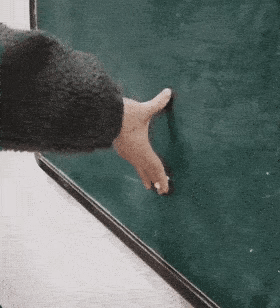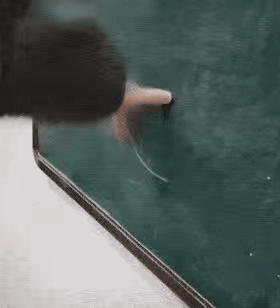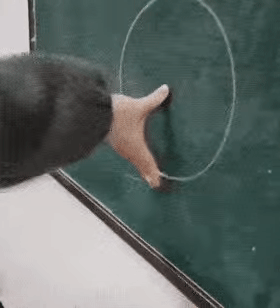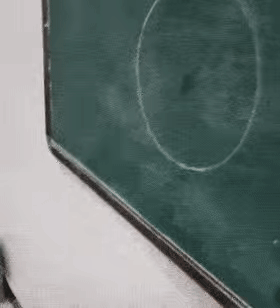
Elementos de um círculo
- Centro: o ponto central do círculo a partir do qual todas as distâncias (raios) são medidas.
- Raio: a distância do centro de um círculo a qualquer ponto na circunferência.
- Circunferência: a linha curva que forma a fronteira do círculo, composta por todos os pontos a uma distância igual do centro.
- Diâmetro: o dobro do raio. Ou seja, o diâmetro é uma linha que atravessa o centro do círculo e liga dois pontos opostos da circunferência.
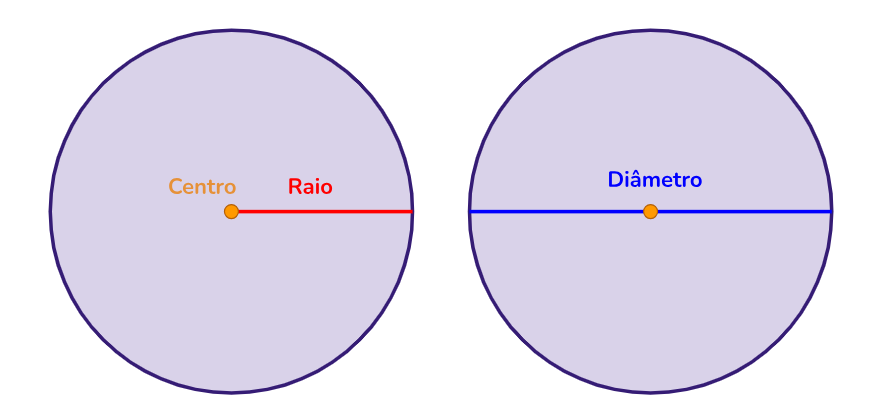
Perímetro do círculo: corresponde ao comprimento da circunferência de mesmo raio. A medida do comprimento C de uma circunferência de raio r é dada por:
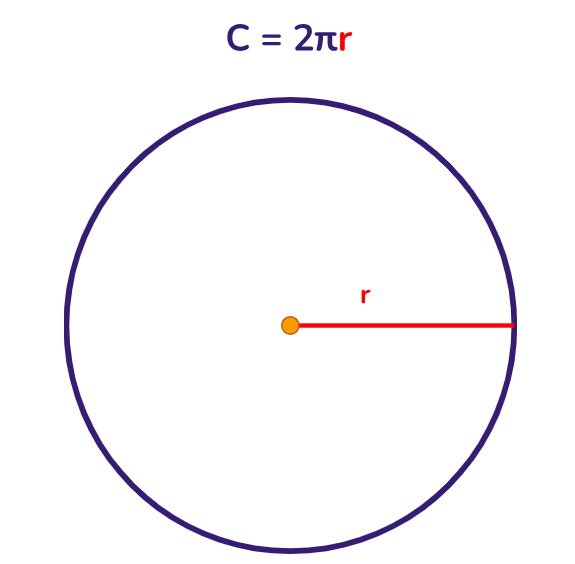
Área do círculo: é a medida de sua região interior. Em um círculo de raio r, sua área A é dada por
Trapézio
Um trapézio é um polígono de quatro lados em que pelo menos um par de lados é paralelo, mas os outros dois lados não são.
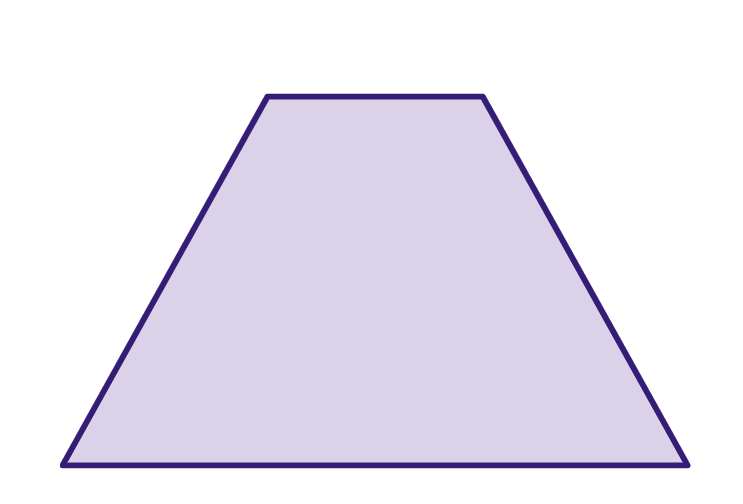
- Lados e ângulos: um trapézio tem quatro lados e quatro ângulos. Os dois lados que são paralelos são chamados de bases, enquanto os outros dois lados são chamados de pernas ou não paralelos. As bases podem ter diferentes comprimentos, e as pernas também podem ter diferentes comprimentos.
- Bases: as bases de um trapézio são as linhas paralelas que estão opostas uma à outra. A base mais longa é chamada de "base maior," e a base mais curta é chamada de "base menor."
- Altura: a altura de um trapézio é a distância perpendicular entre as duas bases. A altura é sempre medida entre as bases paralelas.
Os trapézios podem ser classificados em diferentes tipos, dependendo de suas características.
Trapézio retângulo: tem um ângulo reto (90 graus)
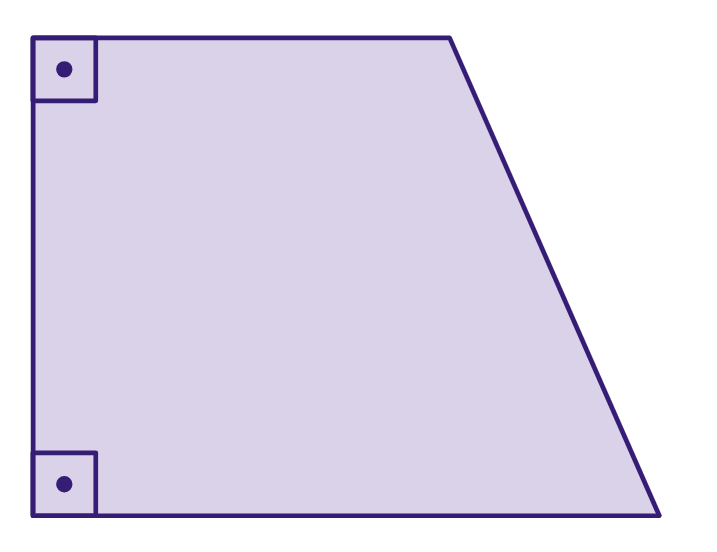
Trapézio isósceles: tem pernas congruentes
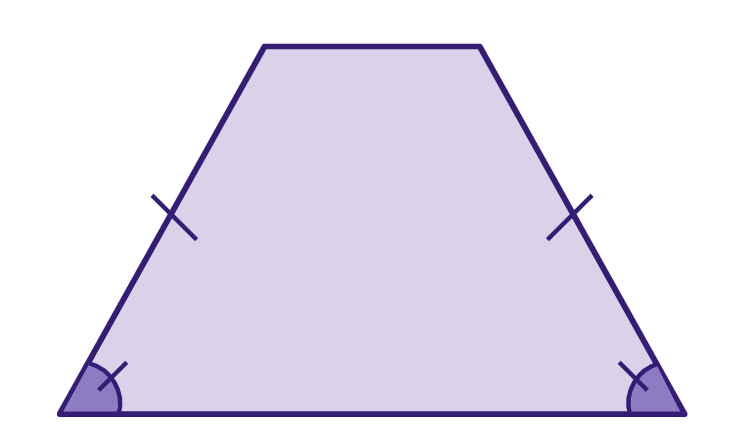
Trapézio escaleno: tem lados de diferentes comprimentos
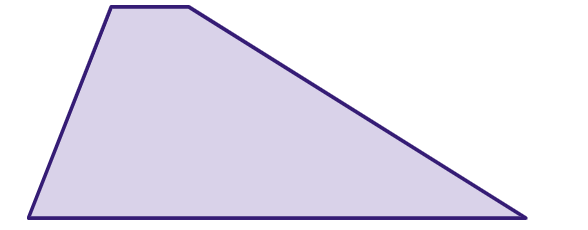
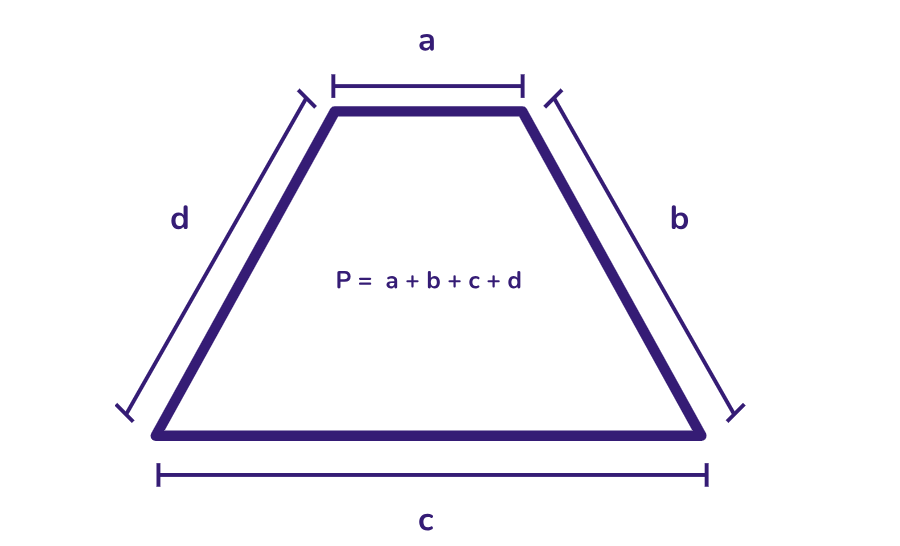
Perímetro do trapézio: é a soma dos comprimentos dos seus quatro lados.
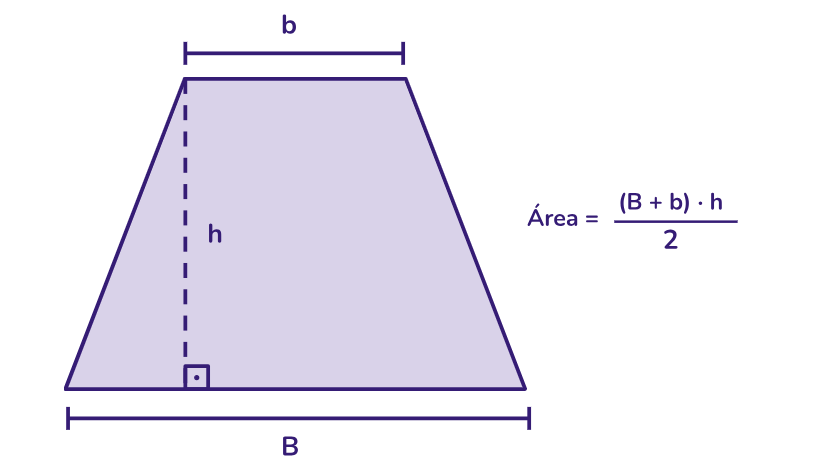
Área do trapézio: pode ser calculada usando a fórmula A = (1/2) * (soma das bases) * altura. A altura é uma linha perpendicular às bases, que liga as duas bases paralelas.
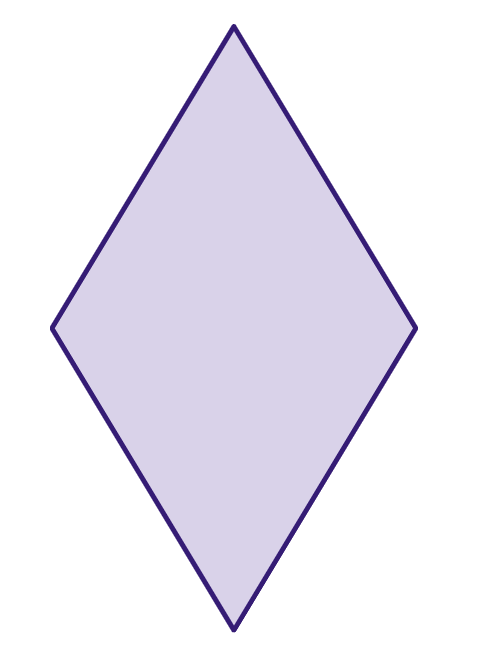
Losango
Um losango é um quadrilátero (um polígono com quatro lados) que tem lados congruentes (todos os lados têm o mesmo comprimento) e ângulos opostos congruentes (todos os ângulos opostos têm o mesmo tamanho).
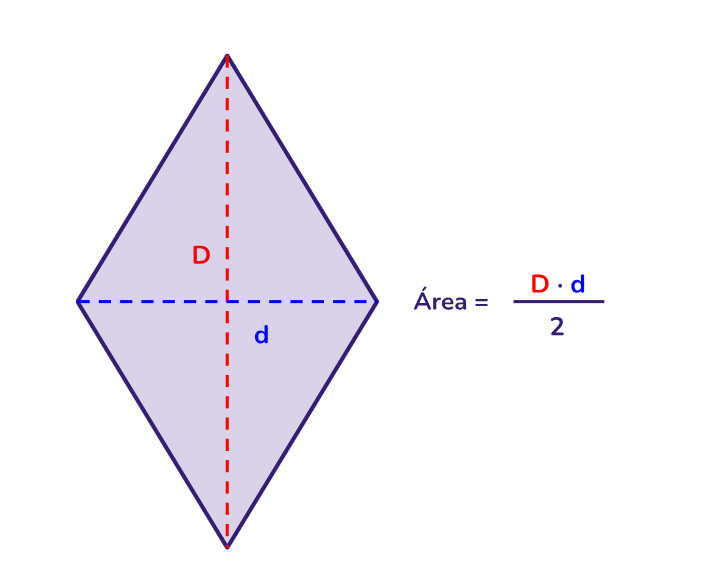
Área do losango: pode ser calculada usando a fórmula A = (diagonal maior * diagonal menor) / 2, onde "A" é a área, e as diagonais são as medidas das duas diagonais do losango. Em um losango, as diagonais são sempre perpendiculares uma à outra.
Perímetro: é a soma dos comprimentos de seus quatro lados.
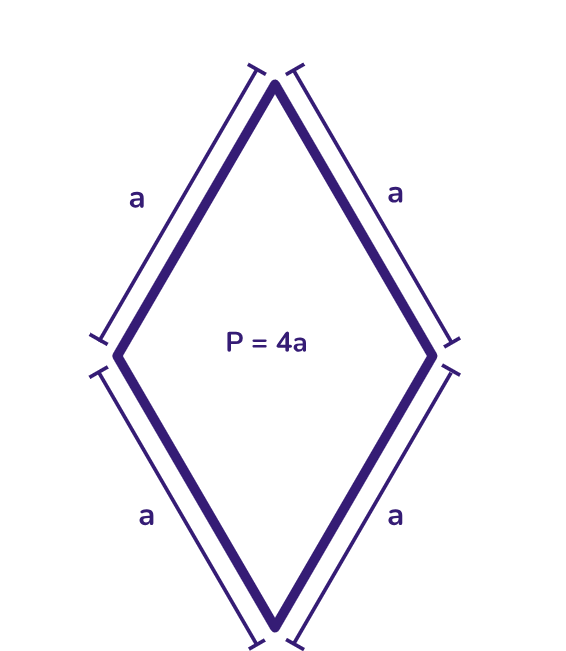
🚨 Todo quadrado é um losango porem nem todo losango é um quadrado. 🚨
Exercícios de geometria plana do Enem e outros vestibulares
Veja alguns exercícios resolvidos de geometria plana:
Exemplo 1
(G1 - IFAL) Julgue as afirmativas abaixo e assinale a alternativa correta.
I. Todo paralelogramo é losango.
II. Se um quadrilátero tem todos os lados com a mesma medida, então esse quadrilátero é um quadrado.
III. As diagonais de um quadrado são perpendiculares entre si.
a) Só I é verdadeira.
b) Só II é verdadeira.
c) Só III é verdadeira.
d) I e III são verdadeiras.
e) II e III são verdadeiras.
Resposta [C]
I) Falsa. Um losango é um paralelogramo de lados todos com a mesma medida.
II) Falsa. Um quadrado deve ter todos os lados com a mesma medida e além disto todos os ângulos devem ser retos.
III) Verdadeira. As diagonais de um quadrado são sempre perpendiculares entre si.
Exemplo 2
(Ufrgs) Assinale a alternativa que apresenta corretamente os valores, na mesma unidade de medida, que podem representar as medidas dos lados de um triângulo.
a) 1 – 2 – 4
b) 3 – 2 – 6
c) 8 – 4 – 3
d) 3 – 9 – 4
e) 6 – 4 – 5
Resposta [E]
Condições para representar um triângulo: “qualquer um dos lados é menor que a soma dos outros dois e maior que o valor absoluto da diferença entre esses lados”. Assim, conseguimos escrever uma expressão matemática da seguinte maneira: "se somar dois lados não pode ser menor que o lado restante".
|4−5|<6<4+5
|4−6|<5<4+6
|5−6|<4<5+6
A única opção que tal condição satisfaz é 6 - 4 - 5.
Exemplo 3
(Enem) Para garantir a segurança de um grande evento público que terá início às 4 h da tarde, um organizador precisa monitorar a quantidade de pessoas presentes em cada instante. Para cada 2.000 pessoas se faz necessária a presença de um policial. Além disso, estima-se uma densidade de quatro pessoas por metro quadrado de área de terreno ocupado. Às 10 h da manhã, o organizador verifica que a área de terreno já ocupada equivale a um quadrado com lados medindo 500m. Porém, nas horas seguintes, espera-se que o público aumente a uma taxa de 120.000 pessoas por hora até o início do evento, quando não será mais permitida a entrada de público.
Quantos policiais serão necessários no início do evento para garantir a segurança?
a) 360
b) 485
c) 560
d) 740
e) 860
Resposta [E]
A área do terreno quadrado de lado 500 m é igual a 5002 = 250.000 m2. Logo, segue que inicialmente estão presentes 250.000 ⋅ 4 = 1.000.000 de pessoas. Ademais, em 16 − 10 = 6 horas, chegarão mais 120.000 ⋅ 6 = 720.000 pessoas. Portanto, a resposta é (1.720.000)/(2.000)=860