Razão e proporção: propriedades e exercícios

Razão e proporção são conteúdos chave para todo o estudo da matemática e são a base para a regra de três, seja ela simples ou composta. Esses conteúdos também definem relações entre grandezas, e uma de suas finalidades é encontrar proporções de objetos, medidas, entre outros.

Para entender bem razão e proporção é necessário que você já tenha conhecimentos sobre frações para poder sair desse artigo com vontade de saber ainda mais!

O que é uma razão?

Preliminarmente, uma razão é uma fração entre dois números ou grandezas a fim de obtermos uma relação comparativa entre eles. Isso ocorre, pois, a divisão é a maneira mais intuitiva de relacionar dois números ou grandezas.

Na teoria, a razão entre duas grandezas, dadas como números reais, A e B, em que B é diferente de 0, é o quociente da divisão de A por B. Na prática, a razão entre A e B é:

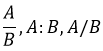
Dizemos que A é o numerador da fração ou antecedente da razão. Ademais, o número B é o denominador da fração ou consequente da razão.

OBS: A razão é usada para exprimir a relação entre as duas grandezas, dessa forma, a razão entre A e B e a razão entre B e A, ou seja: ou podem ter valores diferentes, porém, ambas podem ser usadas dependendo da situação.

Exemplos:

• , ou seja, 0,428 é o número aproximado da razão entre 3 e 7;

• , isto é, 3,2 é a razão entre 16 e 5;

• , em outros termos, 2 é a razão entre os números 8 e 4.

• A razão entre a distância e o tempo informa quantos metros/quilômetros foram percorridos em um segundo/hora. Isso nada mais é que a velocidade média como conhecemos.

Entenda mais sobre proporção

Agora que você já sabe sobre razão, resta saber sobre a proporção. Portanto, a proporção nada mais é do que uma igualdade entre duas razões. De maneira teórica, se uma razão A por B e outra razão C por D são iguais, dizemos que há proporção entre elas. Por outro lado, de maneira prática temos que a proporção entre duas razões é:

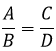
Observando a proporção das razões acima, dizemos que os extremos são A e D e os meios são B e C.

OBS: Os numeradores e denominadores das duas razões não são necessariamente iguais. Além disso, se fossem iguais, estaríamos falando de uma mesma razão. Também, é importante saber que uma proporção pode ser feita por mais de duas razões.

Exemplo:

• , dizemos que a razão três quartos é proporcional a razão dezoito para vinte quatro. Melhor ainda, temos uma proporção, no qual, três está para quatro, assim como, dezoito está para vinte e quatro.

• “Toda manhã eu acordo, escovo os meus dentes e tomo café com leite na proporção de 2 para 3”, analisando esse trecho vemos que a pessoa toma café com leite na proporção de 2 para 3, ou seja, para cada duas determinadas quantidades de café a pessoa coloca três para leite, portanto, para qualquer tamanho da xícara que ela tome, temos a mesma proporção.

Conheça as propriedades da razão e proporção

Ao reescrevermos uma proporção de maneira algébrica, isto é, modificarmos a sua estrutura original sem desequilibrar a igualdade, observamos diversas propriedades. Dessa maneira, a seguir vemos algumas propriedades das proporções:

1. O produto dos extremos é igual ao produto dos meios.

Reescrevendo a proporção pela propriedade acima, então:

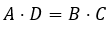
Essa propriedade da matemática é conhecida como “multiplicação em ‘xis’” ou “multiplicação cruzada”. Porém, isso nada mais é do que multiplicar ambos os lados da proporção por :

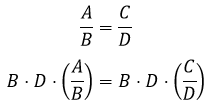
Simplificando os lados da igualdade temos:

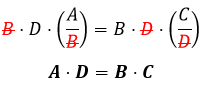
2. Troca de posição entre os extremos.

Essa propriedade nos diz que  e, da mesma maneira como a primeira propriedade usamos a “multiplicação cruzada” para chegarmos a esse resultado. Em outros termos, multiplicamos a proporção  por :

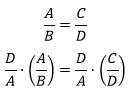
Ao fazer as possíveis simplificações obtemos como resultado:

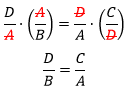
3. Troca de posição entre os meios.

De forma análoga a propriedade 2, temos que . Como você já deve ter imaginado, essa igualdade deriva da “multiplicação cruzada” também. Melhor dizendo, é o produto de por .

4. Frações equivalentes.

Se uma fração é equivalente a uma fração reduzida, então, elas são proporcionais. Em outras palavras, isso ocorre porque uma fração equivalente é uma fração reduzida que foi multiplicada tanto o numerador quanto o denominador pelo mesmo número.

Exemplo:

é a fração reduzida de , ou seja,  e  são proporcionais.

Razão e proporção: o que são grandezas diretamente ou inversamente proporcionais?

Duas grandezas são proporcionais quando uma grandeza se altera e, por conta disso, outra grandeza também se altera.

Grandezas diretamente proporcionais

De forma teórica, dizemos que duas grandezas, a e b, são diretamente proporcionais se , em que k é a constante de proporcionalidade, isto é, a constante que garante que a e b são proporcionais. Em outras palavras, se a é diretamente proporcional a b, então significa dizer que ao aumentar o valor de a, então o valor de b aumenta na mesma proporção. Da mesma forma, se diminuirmos o valor de a, então o valor de b diminui proporcionalmente.

Exemplo:

Maria foi fazer um bolo de chocolate e viu que na receita ia quatro ovos, três xícaras de farinha, uma xícara de achocolatado em pó, etc. Porém, ao procurar os ingredientes, ela encontrou apenas três ovos. Sem desanimar ela conseguiu separar corretamente de forma proporcional a quantia, em xícaras, de farinha e achocolatado em pó para a receita com três ovos. Quantas xícaras de farinha e achocolatado em pó Maria separou?

Resolução:

No enunciado do exercício, a receita de Maria tinha que para três xícaras de farinha iam quatro ovos e para uma xícara de achocolatado em pó iam quatro ovos também, ou seja:

Como são 3 xícaras de farinha para 4 ovos, a constante proporcional é igual a . De forma análoga, a constante proporcional do achocolatado em pó para os ovos é igual a .

Sabendo que constantes proporcionais garantem a proporção e que Maria irá fazer a receita com 3 ovos, então:

Isolando as variáveis:

Portanto, Maria precisou de 2 xícaras mais um quarto de xícara de farinha e três quartos de xícara de achocolatado em pó para fazer a mesma receita com três ovos.

Analisando o exemplo, podemos perceber que para que a receita desse certo, as grandezas ‘quantia de ovos’ e ‘xícaras de farinha’ devem ser diretamente proporcionais. Assim como, a ‘quantia de ovos’ tinha que ser diretamente proporcional com ‘xícaras de achocolatado em pó’. Pois, se diminuirmos a quantia de ovos, a quantia de xícaras de farinha e xícaras de achocolatado em pó devem diminuir proporcionalmente também, para que a receita não fique com mais farinha e achocolatado em pó do que o normal.

Grandezas inversamente proporcionais

Por outro lado, temos as grandezas que são inversamente proporcionais. Em suma, duas grandezas, a e b, são inversamente proporcionais se , em que k é a constante que garante a proporcionalidade. Perceba que grandezas inversamente proporcionais se multiplicam para gerar a constante, já as grandezas diretas se dividem. Isso ocorre, pois, se a é inversamente proporcional a b, significa que ao aumentarmos o valor de a, o valor de b deve ser diminuído proporcionalmente. De forma análoga, ao diminuir o valor de a, o valor de b deve ser aumentado.

Exemplo:

Uma casa será construída em 180 dias com 15 trabalhadores. O dono da casa está ficando com suas dívidas apertadas e, por isso, diminuiu a quantidade de trabalhadores para 10. Dessa forma, em quantos dias os 10 trabalhadores terminaram a construção (considerando que cada trabalhador tem o mesmo rendimento)?

Resolução:

Pelo enunciado, o dono da casa esperava a casa pronta em 180 dias para 15 trabalhadores. Analisando de forma lógica, ao diminuir a quantia de trabalhadores, então o serviço demorará mais para terminar. Ou seja, diminuindo a quantidade de trabalhadores irá aumentar os dias para a casa ficar pronta. Dessa forma, temos duas grandezas inversamente proporcionais e, portanto:

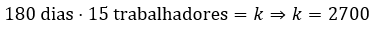
Analisando a proporcionalidade, temos que a constante proporcional é igual a . Dessa maneira, ao diminuirmos o número de trabalhadores, o número de dias vezes o novo número de trabalhadores deverá dar o mesmo resultado k:

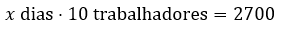
Isolando a grandeza dos dias:

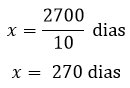
Portanto, diminuindo o número de trabalhadores para 10, a casa ficará pronta em 270 dias.

Perceba que para seguir a lógica, ao diminuir o número de trabalhadores é necessário e natural que demore mais tempo para uma construção ficar pronta. Consequentemente, uma grandeza diminui e outra aumenta e, dessa forma, temos que elas são inversamente proporcionais.

Agora que você leu o artigo até aqui, que tal resolver os exercícios de razão e proporção abaixo para exercitar o seu conhecimento?

Hora de treinar: exercícios de razão e proporção

1. Em uma aula de dança, a razão entre o número de homens para o número de mulheres é de quatro para sete. Quantos homens e mulheres estão nessa aula se no total temos 44 pessoas?

a) 10 homens e 34 mulheres.

b) 16 homens e 28 mulheres.

c) 20 homens e 24 mulheres.

d) 14 homens e 30 mulheres.

e) 12 homens e 32 mulheres.

Resolução:

Pelo enunciado, para qualquer número de homens e mulheres a razão entre o homem e a mulher é quatro para sete, isto é, temos a seguinte proporção:

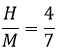
Além disso, temos que se temos 44 pessoas isso significa que o número de homens mais o número de mulheres é igual a 44, portanto:

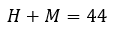
Com base nas duas equações descobertas, podemos construir um sistema com essas duas variáveis, então, obtemos:

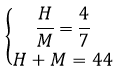
Para resolver o sistema acima, podemos isolar uma das letras e substituir na outra equação:

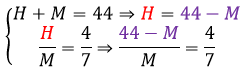
Ao isolarmos o H, obtemos na segunda equação . Para resolve-la, podemos usar a propriedade de que o produto dos extremos é igual ao produto dos meios, ou seja:

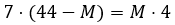
Agora resta apenas simplificar os resultados:

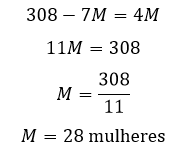
Sabendo o número de mulheres podemos encontrar logicamente que o número de homens é o total menos o número de mulheres, ou seja, 44 – 28 = 16 homens. Dessa forma, a resposta é a alternativa B.

2. Uma pequena empresa resolveu dar um bônus salarial aos seus três funcionários e, para isso, desembolsou R$ 840,00. Sabe-se que o Alex trabalha 30 horas por semana, Bruno trabalha 35 horas por semana e Carlos trabalha 40 horas semanais. Dessa forma, quantos reais Alex, Bruno e Carlos receberão, respectivamente, se a divisão da empresa for proporcional as horas trabalhadas?

a) R$230,00; R$295,00; R$315,00

b) R$235,00; R$290,00; R$315,00

c) R$245,00; R$270,00; R$325,00

d) R$240,00; R$280,00; R$320,00

e) R$255,00; R$275,00; R$310,00

Resolução:

Interpretando o enunciado, podemos notar que a quantia que cada um receberá será diretamente proporcional a quantia de horas trabalhadas por semana. Portanto, temos uma constante proporcional que será igual ao bônus salarial de cada funcionário pelas horas que eles trabalham por semana. Melhor dizendo:

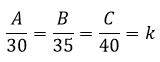
Com a proporção acima, podemos chegar a três conclusões ao usarmos a “multiplicação em ‘xis’”:

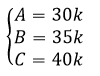
Além disso, o enunciado disse que a empresa disponibilizará R$ 840,00 para o bônus. Sendo assim, a soma dos bônus salariais dos três funcionários é igual a 840 reais:

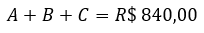
Substituindo os valores A, B e C pelas igualdades feitas anteriormente, obtemos:

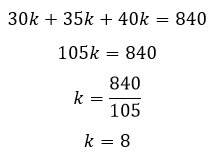
Se a constante proporcional é igual a 8, basta substituir seu valor nas três igualdades (A = 30k, B = 35k e C = 40k):

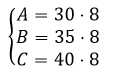
Dessa forma, cada funcionário receberá:

Sendo assim, a única alternativa que garante as igualdades é a letra D.

3. O cálculo que um clube de futebol realiza para exibir o desempenho (D) de cada jogador a cada treino é diretamente proporcional ao tempo de treino (t), intensidade (i) e sua boa alimentação diária (a). Além disso, é inversamente proporcional a sua desatenção (d) e a seu desequilíbrio emocional (d_e). A constante que garante a proporcionalidade dessas grandezas é o IMC (k) de cada jogador. Com essas informações, a fórmula que o clube utiliza para calcular o desempenho é:

a)

b)

c)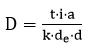

d)

e)

Resolução:

Pelo enunciado, a questão pede o valor de D, sabendo que ele é diretamente proporcional ao tempo (t), intensidade (i) e boa alimentação (a) e inversamente proporcional ao desequilíbrio emocional (d_e) e a desatenção (d). Além disso, o enunciado nos diz que a constante que garante a proporcionalidade é o IMC (k) de cada jogador, ou seja, para cada proporção de D com as suas grandezas tem como constante o IMC (k).

Dessa forma, sabendo que diretamente proporcional é quando uma grandeza e outra aumentam ou diminuem proporcionalmente. Ademais, inversamente proporcional é quando uma grandeza aumenta e outra diminui, ou vice-versa, proporcionalmente, obtemos:

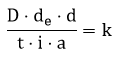
Como o enunciado pede a fórmula do desempenho, então ao isolarmos D, o resultado fica:

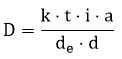
Sendo assim, a alternativa A é a correta.

Conhecer as propriedades e cálculos matemáticos é importante para alcançar melhores resultados no Enem e nos vestibulares. Então, defina suas estratégias e dedique-se, você vai se sair bem!

👉 Leia também:

Juros compostos: veja como calcular, fórmulas e exemplos práticos

Regra de três simples: saiba tudo sobre o assunto