Soma de frações: como funciona

Para entender a soma de frações é necessário lembrar os conhecimentos sobre a fração.

Frações

Frações são números que representam partições de algum número em determinadas parcelas iguais. A notação mais usada para representar frações é uma barra horizontal, em que o numerador é o número que localiza-se na parte superior da barra e representa o dividendo; já o denominador localiza-se embaixo da barra e simboliza em quantas parcelas o numerador será dividido. Conforme a ilustração:

\[ \dfrac{\text{numerador}}{\text{denominador}} \]

Exemplo:

• A fração \( \dfrac{1}{5} \)é chamada de um quinto e significa que o número inteiro um (numerador), foi dividido em exatamente cinco partes iguais (denominador). Além disso, essa fração representa o número decimal \(0,2\), pois se multiplicarmos ele por \(5\), teremos o número inteiro \(1\) novamente. Caso queira relembrar o assunto, você pode conferir nosso Blog sobre o que são números inteiros.

Perceba que todos os números decimais racionais podem ser representados por alguma fração e, como já deve ter imaginado, não somente uma, mas infinitas representações.

Lembre-se que a fração \( \dfrac{6}{4} \) é igual a \(1,5\), portanto, qualquer fração que represente \(1,5\) é, pela lógica, igual a fração \( \dfrac{6}{4} \). Exemplos:

\[ \dfrac{6}{4} = \dfrac{3}{2} = \dfrac{12}{8} = \dfrac{60}{40} = \dfrac{30}{20} = \dfrac{6 \cdot k}{4 \cdot k} \]

Note que para uma fração ser equivalente a alguma outra fração, o numerador e denominador devem ser multiplicados pelo mesmo número.

Simplicação de Fração

Como falado anteriormente, qualquer número decimal racional tem infinitas representações fracionárias e, dessa maneira, a simplificação de fração é usada para determinar a menor fração inteira possível, tanto no numerador como no denominador.

Para isso, devemos ir dividindo o numerador e o denominador por um número, de forma que ao dividir o numerador e o denominador por esse número ambos resultem em números inteiros. Dividimos novamente por outro número ou pelo mesmo número até que não seja possível realizar as duas divisões simultaneamente pelo mesmo número.

Exemplo:

\[ \dfrac{30}{40} \]

Perceba que essa fração é equivalente a outras frações e podem ser simplificadas pelo mesmo número (\(2\), \(5\) ou \(10\)). Ao dividir o numerador e denominador por \(2\), obtemos:

\[ \dfrac{30 \div 2}{40 \div 2} = \dfrac{15}{20} \]

Ademais, quinze e vinte são múltiplos de cinco, portanto:

\[ \dfrac{15 \div 5}{20 \div 5} = \dfrac{3}{4} \]

Dessa forma, como três e quatro não apresentam nenhum divisor em comum, dizemos que \(\dfrac{3}{4} \) é a fração irredutível que representa o número decimal \(0,75\).

Soma de Frações

Até agora vimos apenas o que é uma fração, seus componentes, suas equivalências e como simplificar uma fração para a forma reduzida. Porém, agora vem a parte das frações que grande parte das pessoas sentem dificuldade, como somá-las?

Sabemos que uma fração é um número que foi dividido uma quantidade determinada de vezes, tomamos o número 1 como exemplo:

Digamos que esse retângulo acima, fosse dividido em três partes iguais, dessa forma, obteríamos:

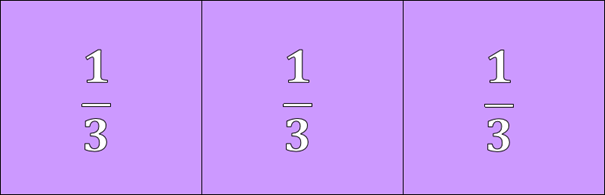
Perceba que ao somarmos as três partes, devemos obter \(1\) novamente, ou seja, \( \dfrac{1}{3} + \dfrac{1}{3} + \dfrac{1}{3} = 1 \), isto é uma soma de frações com denominadores iguais.

Por outro lado, ao dividirmos o retângulo em três partes distintas, obtemos:

Note que não importa a divisão que fizemos do retângulo, a soma de todas as partes continua sendo um e, portanto, \( \dfrac{1}{2} + \dfrac{2}{5} + \dfrac{1}{10} = 1 \). Em contraponto com a outra situação, aqui temos uma soma de frações em que os denominadores são diferentes.

A soma de frações pode ter duas situações: quando os denominadores são iguais ou quando os denominadores são diferentes. Veremos agora como efetuar a soma em cada um dos casos.

Soma de Frações com Denominadores Iguais

            Essa situação é a mais fácil e prática para resolver, pois se os denominadores de uma soma de frações são idênticos, basta somar os numeradores e manter o mesmo denominador, ou seja:

\[ \dfrac{x}{a} + \dfrac{y}{a} = \dfrac{x+y}{a} \]

Exemplo 1:

Tornamos a soma \( \dfrac{2}{5} + \dfrac{6}{5} + \dfrac{3}{5} \) como exemplo. Como falado anteriormente, se os denominadores são iguais, basta realizar a soma dos numeradores e manter o mesmo denominador, isto é:

\[ \dfrac{2}{5} + \dfrac{6}{5} + \dfrac{3}{5} = \dfrac{2 + 6 + 3}{5} = \dfrac{11}{5} \]

Dessa maneira, a fração \( \dfrac{11}{5} \) é a fração que representa a soma dos números \( \dfrac{2}{5} + \dfrac{6}{5} + \dfrac{3}{5} \).

Exemplo 2:

Vejamos a subtração \( \dfrac{13}{8} - \dfrac{3}{8} - \dfrac{1}{8} \) como exemplo.

Já sabemos somar frações com denominadores iguais, mas e subtrair? Funciona da mesma forma, afinal a subtração nada mais é que a soma de dois números, sendo um deles negativo. Ou seja, \( \dfrac{13}{8} - \dfrac{3}{8} \) é o mesmo que \( \dfrac{13}{8} + \left( \dfrac{3}{8} \right) \).

Dessa forma, como temos denominadores iguais, basta realizarmos as operações com o numerador e manter o denominador.

\[ \dfrac{13}{8} - \dfrac{3}{8} - \dfrac{1}{8} = \dfrac{13 - 3 - 1}{8} = \dfrac{9}{8} \]

Assim, \( \dfrac{9}{8} \) é o fração irredutível que representa a subtração \( \dfrac{13}{8} - \dfrac{3}{8} - \dfrac{1}{8} \).

Soma de Frações com Denominadores Diferentes

Por outro lado, se a soma das frações com denominadores iguais é simples e prática, a soma com denominadores diferentes requer um pouco mais de atenção.

Primeiramente, vamos relembrar que uma fração possui várias equivalências, exemplo: a fração \(\dfrac{1}{2}\) pode ser representada por \( \dfrac{2}{4}, \dfrac{4}{8}, \dfrac{10}{20} \), etc. Ademais, é importantíssimo que você saiba encontrar o MMC (mínimo múltiplo comum) entre dois ou mais números para podermos prosseguir com a soma de frações com denominadores diferentes. Se você desejar, pode relembrar o que é MMC e como encontrá-lo em outro post aqui do Blog.

Baseando-se nessas considerações, vamos realizar a seguinte soma de frações:

\[ \dfrac{5}{8} + \dfrac{17}{16} \]

A soma acima possui duas frações com denominadores distintos, dessa forma, não podemos apenas somar os numeradores. Em consequência disso, devemos deixar as frações com o mesmo denominador, para poder somar os numeradores. Com base nisso, sabendo que para uma fração ser equivalente a outra, devemos multiplicar o numerador e o denominador pelo mesmo número, podemos obter a seguinte igualdade:

\[ \dfrac{5}{8} + \dfrac{17}{16} = \dfrac{5 \cdot \color{red}{x}}{8 \cdot \color{red}{x}} + \dfrac{17 \cdot \color{red}{y}}{8 \cdot \color{red}{y}} \]

Assim, a soma de frações com denominadores distintos tem duas etapas: igualar os denominadores e somar os numeradores.

Para igualar os denominadores de frações distintas usamos o MMC dos denominadores. Dessa forma, como MMC(8, 16) = 16, então o denominador final da fração será 16. Portanto, utilizando essa informação e a igualdade feita anteriormente, temos:

\[ \begin{cases} 8\color{red}{x} = 16 \\ 16\color{red}{y} = 16 \end{cases} \]

Isolando as variáveis, sabemos que \(x\) é igual a \(2\) e \(y\) é igual a \(1\), portanto, ao substituir na igualdade, obtemos:

\[ \dfrac{5 \cdot \color{red}{2}}{8 \cdot \color{red}{2}} + \dfrac{17 \cdot \color{red}{1}}{16 \cdot \color{red}{1}} = \dfrac{10}{16} + \dfrac{17}{16} \]

Perceba que agora os denominadores são iguais, portanto, basta somar os numeradores e obter o resultado:

\[ \dfrac{10}{16} + \dfrac{17}{16} = \dfrac{10 + 17}{16} = \dfrac{27}{16} \]

Logo, a fração \( \dfrac{27}{16} \) representa a soma das frações \( \dfrac{5}{8} + \dfrac{17}{16} \). E então, já está craque em frações? Comenta aqui pra gente!