Números inteiros: o que são eles e como aparecem na Matemática?

O que são números inteiros? Como eles são representados na Matemática? Podemos considerar números inteiros aqueles positivos e negativos, que não contenham parte decimal, e o zero. Mas, antes de tratar desse assunto com mais profundidade, vamos relembrar o que são os números naturais? Assim, entenderemos melhor os números inteiros.

Números naturais

Os números naturais são os que mais usamos no nosso cotidiano e, provavelmente, os primeiros números que você conheceu! Esses números são, basicamente, representados pelo conjunto que inicia em zero e seus sucessores: um, dois, três e até o infinito. Dessa forma, usaremos as notações de conjuntos para representá-lo:

N={0, 1, 2, 3, 4, 5, …}

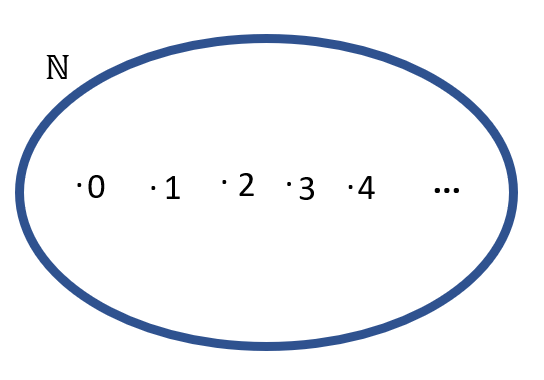
Observação: Há uma divergência entre os matemáticos sobre considerar ou não o número zero um elemento do conjunto dos naturais, no entanto isso é um assunto para outra leitura.

Números inteiros

Agora que já recordamos os números naturais estamos prontos para ir adiante, sabe por quê? Porque o conjunto dos números inteiros é formado pela união do conjunto dos números naturais com todos os seus opostos aditivos.

(Calma, você já vai entender!)

Oposto aditivo de um número é o número que somado com ele resulta em zero. Por exemplo: 3 + (oposto aditivo) = 0.

O único número capaz de fazer essa conta fechar é próprio número, porém com o sinal inverso. Assim, no caso do nosso exemplo é o número -3.

Em outras palavras, o conjunto dos números inteiros é a união dos números naturais com os naturais negativos. Usamos o símbolo Z para representá-lo e escrevemos da seguinte forma:

Z={…,-4,-3,-2,-1, 0, 1, 2, 3, 4, …}

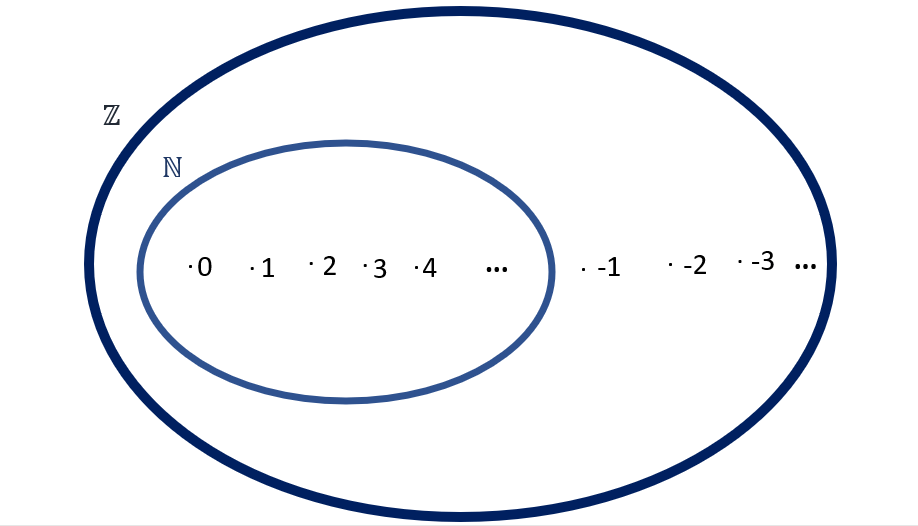
Exemplos: -1000, -5, -1, 0, 22, 940, 100000.

Relação de inclusão

Note que o diagrama que representa os naturais está dentro do diagrama dos números inteiros. Portanto dizemos que o conjunto dos naturais está contido no conjunto dos números inteiros.

Representação na reta

Além disso, podemos representar o conjunto dos números inteiros através da reta numérica, onde os pontos fechados simbolizam os elementos do conjunto e as flechas para esquerda e para a direita nos informam que esse conjunto é infinito, tanto no sentido dos números positivos, quanto no sentido dos números negativos.

Note que quanto mais à direita o número está posicionado na reta, maior ele é. Portanto o número 0 é menor que o 1, 1 é menor que o 2, o 2 é menor que o 3 e assim sucessivamente. Também o -3 é menor que o -2, o -2 menor que o -1 e -1 menor que o 0.

Maior inteiro e menor inteiro: eles existem?

Analisando a reta numérica, é possível fazer a seguinte pergunta: existe um número inteiro maior que todos os outros? Ou ainda: existe um menor que todos os outros? A resposta é não para ambas as perguntas. Pois, ao apontar um número como o menor inteiro, haverá outro menor ainda!

Assim, também não existe um inteiro maior que todos os outros. Dessa forma, o conjunto dos números inteiros não possui supremo e também não possui ínfimo por ser um conjunto com número ilimitado de elementos.

Quantos números inteiros existem?

Outra pergunta interessante é: quantos números inteiros existem? E a resposta é muito simples, o conjunto dos números inteiros é infinito. Dessa forma, o número de elementos entre eles também é.

Operações com números inteiros

Adição e subtração

Na adição e na subtração de números inteiros, é necessário observar os sinais dos números. Se os números tiverem sinais iguais, somam-se os números e mantém-se o sinal. Exemplos:

• (+4) + (+7) = +11
• (-3) + (-2) = -5

Entretanto, se os números tiverem sinais diferentes, então deve ser feito a subtração deles (maior número – menor número), mantendo o sinal do maior número em módulo.

Exemplos:

• (-8) + (+7) = -1
• (-3) + (+9) = +6

Multiplicação e divisão

Na multiplicação e na divisão também iremos observar os sinais para obter o resultado do cálculo. Logo, quando os números tiverem sinais iguais, o resultado será positivo. Da mesma forma, quando os números tiverem sinais diferentes, o resultado será negativo. Conforme mostra a tabela abaixo:

Expressões com números inteiros

Nas expressões numéricas, começamos verificando se há sinais de associação, ou seja, parênteses ( ), colchetes { } e chaves [ ]. Se houver, resolvemos a expressão na seguinte ordem:

1° Parênteses ( )

2° Colchetes [ ]

3° Chaves { }

Para calcularmos o que está dentro do sinal de associação, seguimos a seguinte ordem de preferência entre as operações:

1° Multiplicação e divisão

2° Adição e subtração

Ah, mas e se a expressão tiver somente operações com o mesmo nível de importância? Neste caso começamos calculando da esquerda para a direita!

Depois de calcularmos o que está dentro do sinal de associação, devemos eliminá-lo. E, para isso, seguimos a seguinte regra:

Se o sinal de positivo (+) aparecer antes dos parênteses, colchetes ou chaves, o sinal do número permanece o mesmo, mas se aparecer o sinal de negativo (-) então o sinal do número será trocado.

Veja um exemplo:

Quanto vale a expressão {5-3.(5+9÷3-3×9)+4]}?

Agora que você tirou suas dúvidas sobre a matéria de números inteiros, é hora de dar o próximo passo nos seus estudos. Conheça o Curso Intensivo Enem do Aprova Total e esteja preparado para o Enem e vestibulares!