Trabalho de uma força: conceito, fórmulas e aplicações

Diferente do que ocorre no dia a dia, o conceito de trabalho na Física está relacionado às transformações de energia, sendo fundamental em várias áreas dessa ciência e presente em diversas situações do cotidiano.

Por exemplo, quando empurramos um carrinho de supermercado, a força que estamos exercendo sobre ele provoca um deslocamento, então nossa força está realizando trabalho sobre o carrinho.

Se soltarmos o carrinho, ele vai continuar andando por inércia, mas o chão exerce uma força sobre ele: o atrito. A seguir, vamos nos aprofundar nesse tema e ver que, a força de atrito realiza um tipo de trabalho que "atrapalha" o movimento.

Além disso, nessa publicação, você também vai aprender o significado de trabalho na Física, como calcular essa grandeza, os tipos de trabalho e verá exemplos de como o Enem e vestibulares cobram esse tema. Bora trabalhar?

O conceito de trabalho na Física

Na Física, trabalho é a transferência de energia entre dois sistemas. Essa transferência ocorre devido à ação de uma força, sendo que o trabalho está relacionado à ação dessa força ao longo de um deslocamento.

Quando um gatinho empurra um celular sobre uma mesa, a força que ele exerce realiza trabalho sobre o celular. Além disso, o atrito com a mesa também realiza trabalho.

Se o gatinho empurrar para além da borda da mesa, o celular vai começar a cair, então outra força estará realizando trabalho sobre ele: seu próprio peso! Se houver resistência do ar, essa força também realizará trabalho sobre o celular em queda.

Nesse sentido, já podemos concluir duas coisas muito importantes:

• Para haver trabalho, é preciso existir força e deslocamento.
• Diversas forças podem exercer trabalho sobre um corpo durante seu deslocamento. Por isso, é comum usarmos a expressão trabalho de uma força, sendo importante identificar de qual força estamos falando.

Fórmulas do trabalho

Já sabemos que o trabalho depende de uma força \( \overrightarrow{F} \) sobre um corpo e de seu deslocamento \( \overrightarrow{d} \). Relacionando os módulos dessas duas grandezas, a fórmula do trabalho é a seguinte:

\[ \tau = F \cdot d \cdot cos(\theta) \]

A letra grega τ (tau) é usada para representar trabalho, mas as letras T e W (de work, no inglês) também são comuns.

Ok, mas o que é esse ângulo θ? É o ângulo formado entre os vetores força e deslocamento. Vamos entender melhor a seguir, quando aprendermos os tipos de trabalho.

Mas sobre a fórmula do trabalho, é necessário prestar atenção ao seguinte:

• Força e deslocamento são grandezas vetoriais. No entanto, na Física, trabalho é uma grandeza escalar (até porque é uma forma de energia, que é uma grandeza escalar). Isso acontece porque é uma grandeza obtida a partir de um produto escalar entre os vetores força e deslocamento. O produto escalar é uma operação entre vetores que resulta em um escalar (número).
• Essa fórmula só vale se a força F for constante, não apenas em módulo, mas também em direção e em sentido.

Unidades de medida do trabalho de uma força

Por ser uma forma de energia, o trabalho de uma força possui as mesmas unidades de medida de energia.

No Sistema Internacional (SI), essa unidade é o joule (J). Outras unidades comuns são a caloria (cal) e unidades múltiplas do joule, como o kilojoule (kJ), que vale 10³ J, e o megajoule (MJ), que vale 10⁶ J.

👉 Leia também:

Fórmulas de Física que você precisa saber para o Enem

Tipos de trabalho na Física

Podemos classificar um trabalho realizado a partir do ângulo θ em nulo, motor ou resistente, o que tem consequências para o quão eficiente a força será na realização de trabalho. Vamos entender melhor!

Trabalho nulo

Existem três situações em que o trabalho na Física pode ser nulo. Pensando na fórmula do trabalho (\( \tau = F \cdot d \cdot cos(\theta) \)), τ = 0 se ocorrer pelo menos um dos seguintes casos:

• F = 0: se a força for nula, então ela não realiza trabalho.
• d = 0: se o corpo não se desloca, então não há realização de trabalho sobre ele.
• cos(θ) = 0: isso ocorre para θ = 90º, como aprendemos em trigonometria. Sendo assim, quando os vetores força e deslocamento forem perpendiculares, essa força não realiza trabalho.

Se qualquer um desses termos for nulo, então o trabalho também será nulo, pois zero multiplicado por qualquer coisa é igual a zero. Veja o exemplo a seguir:

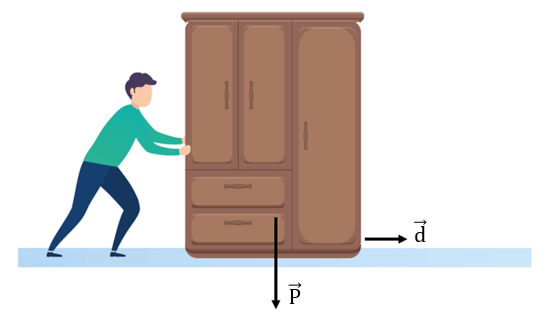
O homem está empurrando um armário, que se desloca para a direita. Podemos pensar em três forças agindo sobre o armário: a força \( \overrightarrow{F} \) que o homem exerce, o peso \( \overrightarrow{P} \) do armário e a força de atrito \( \overrightarrow{F}_{at} \) que o chão exerce sobre o armário.

Perceba que o peso do armário \( \overrightarrow{P} \) é perpendicular ao seu deslocamento \( \overrightarrow{d} \), então, nesse caso, θ = 90º, logo, cos(θ) = 0 e, portanto, τ = 0. Em outras palavras, a força peso não realiza trabalho nessa situação.

Trabalho potente/motor

Chamamos de trabalho motor (ou trabalho potente) aquele em que a força favorece o deslocamento. Matematicamente, um trabalho motor tem sinal positivo.

Veja o caso da força \( \overrightarrow{F} \), que o homem exerce sobre o armário:

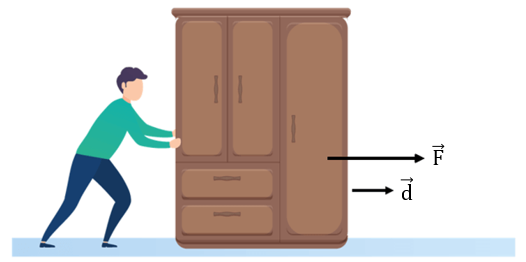
\( \overrightarrow{F} \) tem a mesma direção e o mesmo sentido do deslocamento \( \overrightarrow{d} \), logo, essa força está contribuindo para o deslocamento. Por isso, essa força realiza um trabalho motor.

Esse é um caso particular, pois, como os vetores têm mesma direção e mesmo sentido, θ = 0º, cujo cosseno vale 1. Portanto, na fórmula do trabalho, (\( \tau = F \cdot d \cdot 1 \)), que pode ser escrita simplesmente como (\( \tau = F \cdot d \)).

Se outra pessoa puxasse o armário com uma força \( \overrightarrow{T} \) que forma com o deslocamento \( \overrightarrow{d} \) um ângulo maior ou igual a 0º e menor do que 90º (0º ≤ θ < 90º), o trabalho realizado por essa força também seria motor.

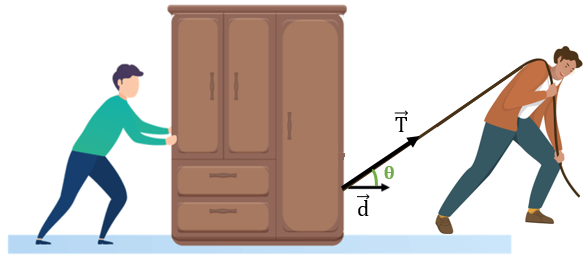
Isso ocorre porque ângulos do primeiro quadrante têm valor positivo de cosseno. Esses ângulos, juntamente com o 0º (cujo cosseno vale 1, como vimos) fornecem valores positivos de trabalho.

No entanto, a força \( \overrightarrow{T} \) possui duas componentes: uma horizontal (\( \overrightarrow{T}_X \)) e uma vertical (\( \overrightarrow{T}_Y \)). Perceba que somente a componente \( \overrightarrow{T}_X \) está na mesma direção do deslocamento, então apenas \( \overrightarrow{T}_X \) realiza trabalho.

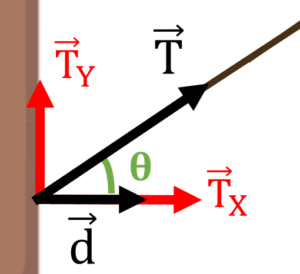
Fazendo uma decomposição vetorial, podemos escrever os módulos de \( \overrightarrow{T}_X \) como \( T \cdot cos(\theta) \) e de \( \overrightarrow {T}_Y \) como \(T \cdot sen(\theta) \). É por isso que o termo \( T \cdot cos(\theta) \) aparece na fórmula do trabalho. Ele informa que, se a força for inclinada, apenas a componente que tem a mesma direção do deslocamento realiza trabalho.

Para um mesmo módulo de força, o maior valor possível de trabalho ocorre quando θ = 0º, pois seu cosseno vale 1, que é o maior valor para o cosseno.

Trabalho resistente

Na Física, chamamos de trabalho resistente aquele em que a força dificulta o deslocamento. Matematicamente, um trabalho resistente tem sinal negativo.

Veja agora o caso da força de atrito \( \overrightarrow{F}_{at} \) que o chão exerce sobre o armário:

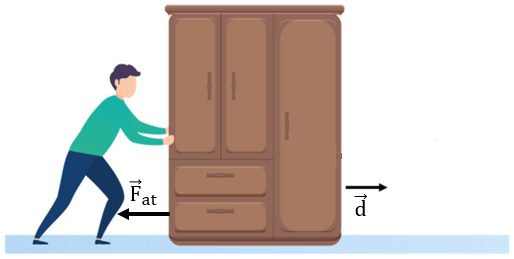
\( \overrightarrow{F}_{at} \) tem a mesma direção e sentido oposto ao do deslocamento \( \overrightarrow{d} \), ou seja, o atrito está atrapalhando o deslocamento. Mesmo que a força que o homem exerce seja suficiente para deslocar o armário, o atrito está dificultando esse deslocamento.

Como os vetores \( \overrightarrow{F}_{at} \) e \( \overrightarrow{d} \) têm mesma direção e sentidos opostos, o ângulo entre eles é θ = 180º, cujo cosseno vale -1.

Analogamente ao caso de θ = 0º, quando θ = 180º, podemos reescrever a fórmula do trabalho como (\( \tau = F \cdot d \cdot (-1) \)) ou, simplesmente, (\( \tau = - F \cdot d \)). Para um mesmo módulo de força, esse é o menor valor possível para o trabalho, já que o menor valor de cosseno é -1.

Sendo assim, quando uma força forma 180º com o deslocamento, é o caso em que ela mais "atrapalha" o deslocamento.

Para ângulos θ tais que 90º < θ ≤ 180º, o trabalho é resistente.

Trabalho de uma força variável

No gráfico abaixo, o eixo das abscissas (eixo x) representa valores de deslocamento e o eixo das ordenadas (eixo y) representa valores de força. Esse gráfico nos diz que uma força constante de 100 N foi exercida sobre algum corpo, deslocando-o ao longo de 100 m.

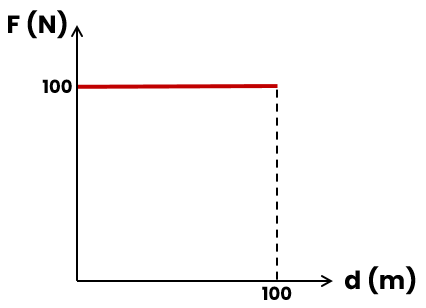
O eixo das forças indica forças que podem realizar trabalho, ou seja, apenas forças que tenham mesma direção do deslocamento d. Do contrário, se for uma força cuja direção é diferente daquela de d, o gráfico indica a componente cuja direção é a mesma do deslocamento.

Como a força F = 100 N é constante, podemos calcular o trabalho usando a fórmula:

\[ \tau = F \cdot d \\ \]

\[ \tau = 100 \cdot 100 \\ \]

\[ \tau = 10.000\ N \]

Consegue perceber que, se calculássemos a área do quadrado formado entre a linha do gráfico e o eixo do deslocamento, seria a mesma coisa que multiplicar o valor de F pelo valor de d? Isso significa que, numericamente, a área é igual ao trabalho realizado por essa força.

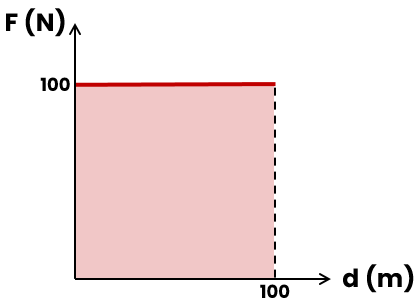
O mais legal é que podemos generalizar isso para qualquer gráfico F × d, incluindo para forças variáveis! Dessa forma, conseguimos calcular o trabalho realizado por uma força variável, algo que não conseguimos usando a fórmula do trabalho.

⚠️ Tome cuidado: se a força for negativa (abaixo do eixo d), significa que ela tem sentido oposto ao do deslocamento, então o trabalho será negativo.

Aplicações e exemplos de trabalho na Física

A fórmula do trabalho que aprendemos ((\( \tau = F \cdot d \cdot cos(\theta) \)) é uma fórmula geral, mas existem situações na Física em que podemos usar fórmulas específicas para determinados tipos de força.

A fórmula geral de trabalho continua sendo válida, mesmo nesses casos, só que podemos usar grandezas específicas para calcular o trabalho. Vamos ver alguns exemplos?

Trabalho da força resultante (teorema da energia cinética)

Lá das leis de Newton, sabemos que a força resultante sobre um corpo é a soma vetorial de todas as forças que atuam sobre ele. Existe um importante teorema que nos dá uma fórmula específica para o trabalho da força resultante.

Esse teorema (chamado teorema da energia cinética ou teorema do trabalho e da energia cinética) nos diz que o trabalho da força resultante sobre um corpo é igual à variação da energia cinética desse corpo.

Para demonstrar esse teorema, vamos partir da equação de Torricelli para um corpo se movendo em movimento uniformemente variado:

\[ v^2 = v_0^2 + 2 \cdot a \cdot \Delta s \]

Vamos chamar o deslocamento Δs de d e isolar o termo a · d:

\[ \frac{v^2 - v_0^2}{2} = a \cdot d \]

Agora, vamos multiplicar os dois lados da equação pela massa m do corpo (calma, isso vai fazer sentido logo em seguida):

\[ m \cdot \frac{v^2 - v_0^2}{2} = m \cdot a \cdot d \]

No lado esquerdo da equação, podemos aplicar a propriedade distributiva, obtendo \( \frac{m \cdot v^2}{2} - \frac{m \cdot v_0^2}{2} \) . No lado direito, veja que o termo m · a, pela segunda lei de Newton, é a força resultante F_R sobre o corpo. Logo:

\[ \frac{m \cdot v^2}{2} - \frac{m \cdot v_0^2}{2} = F_R \cdot d \]

Beleza, mas \( \frac{m \cdot v^2}{2} \) é a fórmula da energia cinética. Além disso, \( F_R \cdot d \) corresponde ao trabalho. Assim, chegamos à expressão do teorema:

\[ \tau _R = \Delta E_C \]

Trabalho da força peso

A força peso é uma força conservativa, ou seja, seu trabalho só depende dos pontos de onde um corpo sai e onde chega, não da trajetória. Para um corpo de massa m, em uma região de gravidade g, que vai de um ponto a outro de altura maior ou menor, com altura h entre esses pontos, o trabalho realizado pela força peso é dado por

\[ \tau _P = m \cdot g \cdot h \]

Essa fórmula é familiar para você? Se você já estudou energia mecânica, lembra-se dela como a fórmula da energia potencial gravitacional!

De fato, o trabalho da força peso é igual, em módulo, à variação de energia potencial gravitacional (E_PG) entre dois pontos separados por uma altura h.

No desenho abaixo, não importa se a caixa cai seguindo a trajetória parabólica da esquerda ou se ela cai verticalmente: se a diferença de altura for a mesma, o trabalho realizado pela força peso é a mesma.

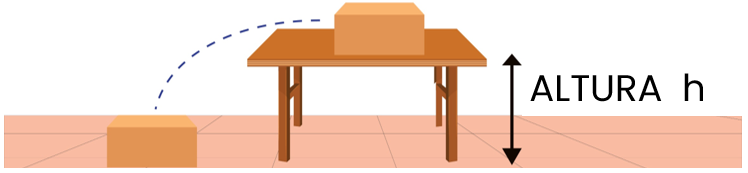
Precisamos tomar cuidado com os sinais:

• Se a caixa desce, o peso (que aponta para baixo) favorece o deslocamento, então o trabalho é motor (positivo).
• Caso a caixa suba, o peso dificulta o deslocamento, então o trabalho é resistente (negativo).

De maneira rigorosa, dizemos que o trabalho da força peso é igual ao negativo da variação de E_PG (\( \tau _P = - \Delta E_{PG}\)). Tá, mas por que o "negativo"? Veja só:

Se a caixa desce, a posição no chão é menor do que a posição na mesa, então a variação de energia potencial gravitacional (ΔE_PG) é negativa. No entanto, o trabalho é positivo, por isso surge o sinal de menos na relação.

Isso vale para forças conservativas em geral: o trabalho realizado por uma força conservativa é igual ao negativo da variação de energia potencial associada.

👉 Leia também:

Energia potencial: confira tipos, fórmulas e resumo

Trabalho da força elástica

Da lei de Hooke, sabemos que a força elástica exercida por um corpo elástico deformado é calculada por \( F_E = k \cdot x \), em que k é a constante elástica (uma grandeza associada ao material, que indica o quão facilmente o corpo se deforma ao sofrer ação de alguma força) e x é a deformação.

Nesse sentido, podemos ver que a força elástica e a deformação são diretamente proporcionais. Se esboçarmos um gráfico da força em função da deformação, teremos um segmento de reta partindo da origem (pois, para F = 0, x = 0):

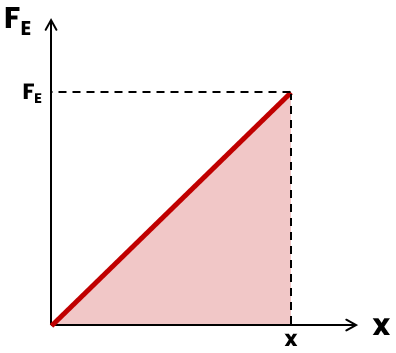
Como vimos anteriormente, a área indicada no gráfico é numericamente igual ao trabalho realizado pela força elástica. Para calcular essa área, devemos considerar a área de um triângulo: (base · altura)/2.

No exemplo do gráfico, em que um determinado valor de força elástica F_E provocou uma deformação x, a base do triângulo vale x e a altura vale F_E. Como F_e =k · x (sendo x a deformação que a força provocou, a mesma deformação x no eixo das abscissas), então podemos substituir F_E por k · x no cálculo da área:

\[ \tau_{F_E} \stackrel{N}{=} A = \frac{x \cdot k \cdot x}{2} \\ \]

\[ \tau_{F_E} = \frac{k \cdot x^2}{2} \]

Em relação aos sinais, imagine o seguinte exemplo: um arqueiro puxa a flecha através da corda do arco e solta, disparando a flecha.

• Ao puxar a corda, o trabalho que a força elástica realiza é resistente (negativo).
• Já ao soltar a corda, o trabalho que a força elástica realiza sobre a flecha é motor (positivo).

Similarmente à E_PG, esse é um caso em que estamos lidando com uma força conservativa (força elástica), então o trabalho realizado pela força elástica é igual ao negativo da variação de energia potencial elástica (E_PE): \( \tau _{F_E} = - \Delta E_{PE} \).

Faz sentido! Afinal, quando o arqueiro puxa a corda, a variação de E_PE é positiva (pois a E_PE aumenta), logo, o trabalho é negativo. Quando a corda dispara a flecha, a variação de E_PE é negativa (E_PE diminui), assim, o trabalho é positivo.

Trabalho da força elétrica

Assim como o peso e a força elástica, a força elétrica também é uma força conservativa. Portanto, seu trabalho independe da trajetória.

Se um corpo de carga q se move de um ponto A para um ponto B, cuja diferença de potencial entre eles é U_AB, podemos calcular o trabalho realizado pela força elétrica com a seguinte fórmula:

\[ \tau_{F_E} = q \cdot U_{AB} \]

Podemos também calcular esse trabalho como o negativo da variação de energia potencial elétrica (E_P) entre os pontos A e B:

\[ \tau_{FE} = - \Delta E_P \]

Trabalho de um gás ideal

Na termodinâmica, aprendemos a calcular o trabalho que um gás realiza ou sofre. Esse trabalho depende da pressão (P) exercida sobre o gás (ou que ele exerce) e de sua variação de volume (ΔV):

\[ \tau = P \cdot \Delta V \]

Isso serve para um modelo de gás ideal confinado em um recipiente cujo volume possa variar (normalmente através de um pistão móvel), como na figura a seguir:

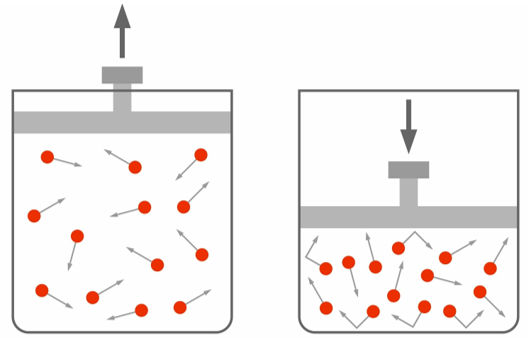
Em relação aos sinais, existe a seguinte convenção:

• Se o gás expande (ΔV positivo), realizando trabalho, o trabalho é positivo.
• Já se o gás é comprimido (ΔV negativo), sofrendo trabalho, o trabalho é negativo.

Dessa forma, só há realização de trabalho se o volume do gás variar. Ah, e você só pode usar a fórmula se a pressão P for constante, ok? Caso contrário, precisamos recorrer ao método da área em um gráfico P × V (pressão versus volume):

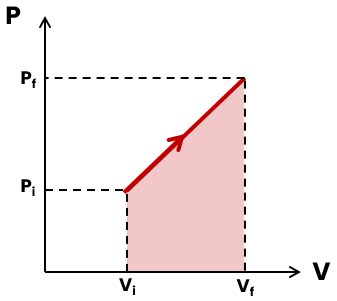
O sentido da seta indica o tipo de processo termodinâmico. No gráfico acima, a seta aponta para cima (indicando que a pressão aumentou) e da esquerda para a direita (indicando que o gás expandiu, ou seja, seu volume aumentou). Por ser uma expansão, o trabalho é positivo. Caso a seta apontasse para o sentido contrário, o trabalho seria negativo.

No caso de ciclos (quando o gráfico forma uma figura fechada), o trabalho corresponde à área da parte interna da figura, como no exemplo abaixo:

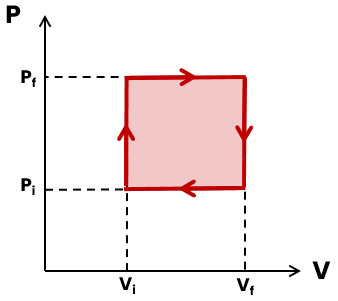
Nesse exemplo, o sentido do ciclo é horário, em que o trabalho é positivo. Se o sentido for anti-horário, o trabalho será negativo.

Resumo: Trabalho na Física

Em síntese, vamos relembrar os pontos mais importantes:

• Na Física, trabalho é a energia transferida por uma força ao deslocar um corpo.
• Fórmula do trabalho: \( \tau = F \cdot d \cdot cos(\theta) \). Unidade de medida no SI: joule (J).
• O trabalho é nulo quando F = 0, d = 0 ou θ = 90º.
• Trabalho motor: favorece o deslocamento e tem sinal positivo.
• Trabalho resistente: dificulta o deslocamento e tem sinal negativo.
• Em um gráfico F × d, a área é numericamente igual ao trabalho.
• Teorema da energia cinética: o trabalho da força resultante é igual à variação da energia cinética, ou seja, \( \tau_R = \Delta E_C \).
• Trabalho da força peso: \( \tau_P = m \cdot g \cdot h \).
• Trabalho da força elástica: \( \tau = \frac{k \cdot x^2}{2} \).
• Trabalho da força elétrica: \( \tau = q \cdot U_{AB} \).
• Trabalho de um gás ideal: \( \tau = P \cdot \Delta V \) ou a área em um gráfico P × V.

Como o trabalho de uma força cai no Enem e vestibular

O Enem não costuma cobrar trabalho diretamente, mas adora questões de energia mecânica e conservação de energia, assuntos que têm a ver com trabalho na Física. A seguir, vamos ver alguns exemplos de perguntas em processos seletivos.

Exemplo de trabalho no Enem

(Enem PPL 2016) Para reciclar um motor de potência elétrica igual a 200 W, um estudante construiu um elevador e verificou que ele foi capaz de erguer uma massa de 80 kg a uma altura de 3 metros durante 1 minuto. Considere a aceleração da gravidade 10,0 m/s². Qual a eficiência aproximada do sistema para realizar tal tarefa?

a) 10%

b) 20%

c) 40%

d) 50%

e) 100%

Resposta: [B]
Para resolver a questão, precisamos conhecer o significado de potência, que a razão entre algum tipo de energia consumida e o intervalo de tempo em que o processo ocorreu.
Como trabalho é uma forma de transferência/consumo de energia, então a potência do motor corresponde à razão entre o trabalho que ele realizou e o tempo de 1 minuto. Calculando o trabalho:
\[ \tau = F \cdot d \\
\tau = 80 \cdot 10 \cdot 3 \\
\tau = 2.400\ J \]
O tempo é de 1 minuto, que corresponde a 60 segundos. Dessa forma, pela ideia de potência:
\[ P = \frac{\tau}{\Delta t} \\
P = \frac{2.400}{60} \\
P = 40\ W \]
A ideia de eficiência corresponde à razão entre o que é utilizado (potência de 40 W) e o que é recebido (potência de 200 W):
\[ \eta = \frac{40}{200} \\
\eta = 0,2 = 20 \% \]

Exemplo de trabalho nos vestibulares

(Uece 2022) Um experimento consiste em analisar o comportamento de um objeto de dimensões desprezíveis que será abandonado a partir do repouso de uma mesa até alcançar o chão percorrendo rampas de diferentes inclinações. O trabalho realizado pela força peso

a) é o mesmo e independe da rampa escolhida.

b) é maior quanto maior a inclinação da rampa.

c) é menor quanto maior a inclinação da rampa.

d) depende da velocidade do objeto.

Resposta: [A]
Como o exercício pede o trabalho da força peso, que é conservativa, ele é o mesmo e independe da rampa escolhida, já que depende somente das posições inicial e final.