Segunda lei de Newton: conceito, exemplos e aplicações

A segunda lei de Newton, também conhecida como princípio fundamental da dinâmica, relaciona a força resultante que atua sobre um corpo com a aceleração adquirida por esse corpo. Além disso, é através dela que obtemos uma das definições mais interessantes para a grandeza física massa.

Relação entre força e aceleração

Segundo a primeira lei de Newton, quando a força resultante sobre um corpo é nula, ele tende a continuar em seu estado de movimento original, seja esse em repouso ou em movimento retilíneo e uniforme.

Tá, mas o que acontece quando existe uma força resultante não nula?

Nesse caso, o corpo adquire uma aceleração. Matematicamente, a relação entre a força resultante aplicada e a aceleração adquirida pelo corpo é dada por:

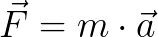
Perceba que, quanto maior for a força exercida sobre o corpo, maior será a aceleração por ele adquirida, ou seja, as duas grandezas são diretamente proporcionais.

Note também que força e aceleração são grandezas vetoriais, ou seja, além de módulo, elas possuem uma orientação (direção e sentido). Como a massa de um corpo é um valor escalar sempre positivo, a direção e o sentido da aceleração de um corpo são sempre idênticos aos da força resultante que atua sobre ele.

Por exemplo, na imagem abaixo, as forças verticais (peso e normal) se anulam e a força resultante é a força F aplicada pela pessoa. Como existe uma força resultante, existe uma aceleração na mesma direção e no mesmo sentido dessa força:

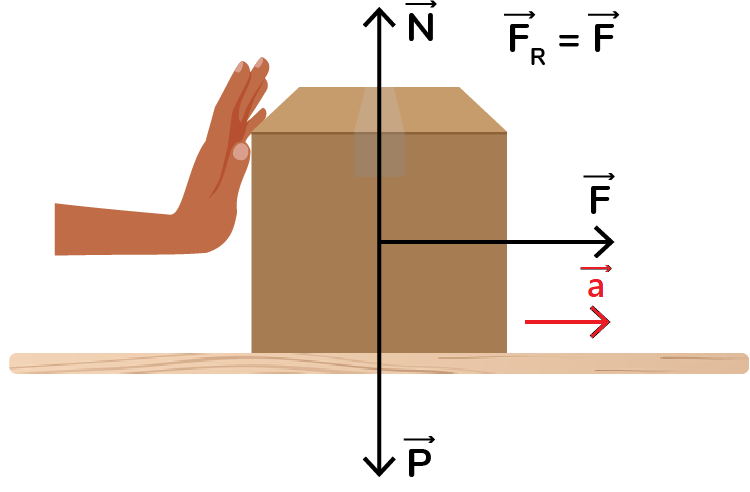
Força peso

Uma aplicação interessante da segunda lei de Newton é a força peso.

Como sabemos, todo corpo próximo da Terra é atraído para ela por uma força gravitacional que chamamos de força peso.

Para calcular o valor da força peso P que atua sobre qualquer corpo, basta aplicar a segunda lei de Newton, utilizando o valor da aceleração da gravidade terrestre g:

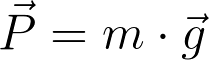
em que g vale aproximadamente 10 m/s².

Vale lembrar que a força peso sempre possui a mesma orientação da aceleração gravitacional terrestre: vertical e para baixo.

Massa inercial

Note que, na fórmula para a segunda lei de Newton, a massa do corpo atua como constante de proporcionalidade. O que isso significa?

Bom, se a mesma força resultante atuar sobre dois corpos de massas diferentes, o mais leve adquirirá uma aceleração maior do que o mais pesado.

Por exemplo, na figura abaixo, 1 N de força foi aplicado sobre duas caixas. A caixa de 1 kg adquiriu 1 m/s² de aceleração, já a caixa de 2 kg adquiriu apenas 0,5 m/s² de aceleração.

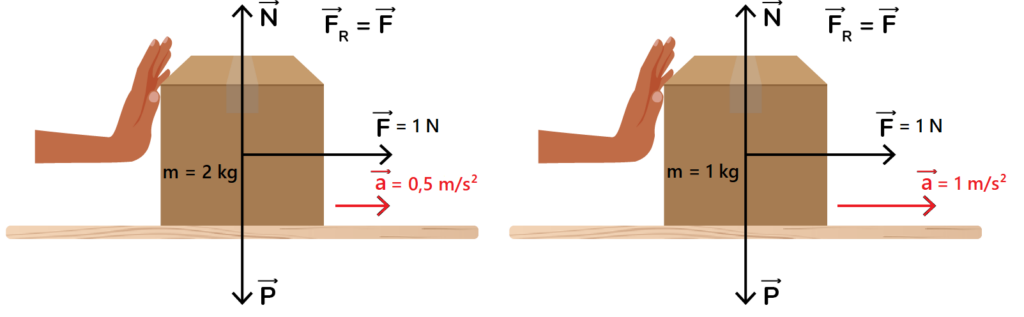
Dessa forma, podemos concluir que a massa de um corpo representa uma medida da sua resistência à mudança de estado de movimento.

Por exemplo, imagine duas bolas sendo atiradas na sua direção a uma mesma velocidade, uma de boliche e outra de tênis, qual delas exigirá uma força maior para ser parada?

Exatamente! A bola de boliche. Isso ocorre pois ela possui mais massa e, portanto, resiste mais à mudança no seu estado de movimento.

Estado de movimento

Como visto, a aplicação de uma força resultante não nula sobre um corpo causa uma aceleração nele. Sendo assim, há uma alteração no estado de movimento desse corpo.

Se uma força atua sobre um corpo em repouso, esse deixará o repouso e entrará em movimento.

Para um corpo que já se encontra em movimento retilíneo e uniforme, a aplicação de uma força faz com que ele entre em um movimento retilíneo uniformemente variado, até que a aplicação da força seja interrompida.

Quer se preparar para o Enem e vestibulares com quem mais entende do assunto? A plataforma Aprova Total é a maior especialista no ensino digital e tem as melhores videoaulas e professores!