Leis de Newton: conceitos, fórmulas e aplicações

As três leis de Newton formam a base da dinâmica, área da Física que estuda o movimento dos corpos e as suas causas. Essas leis foram introduzidas pelo matemático, filósofo, astrônomo e físico Isaac Newton em seu livro Princípios matemáticos da filosofia natural, de 1687.

Considerado um gênio da Ciência, Newton deixou diversas contribuições que permanecem até hoje, como a lei da gravitação universal. A seguir, você vai aprender o significado de cada uma das leis de Newton e verá como o Enem e os vestibulares cobram o assunto.

Primeira lei de Newton

Também chamada de lei da inércia, a primeira lei de Newton é enunciada da seguinte forma:

“Todo corpo tende a permanecer em seu estado de movimento, seja ele movimento retilíneo uniforme ou repouso, a não ser que uma força resultante externa o obrigue a modificar seu movimento”

Em outras palavras, não é necessária a presença de uma força para manter o movimento de um corpo. E isso não é intuitivo! Por séculos, imaginava-se o contrário: se um corpo está em movimento, então obrigatoriamente há uma força atuando sobre ele. Essa ideia foi defendida por pensadores como Aristóteles, o que até faz sentido à primeira vista.

Imagine o seguinte: você dá um empurrão em uma cadeira de rodinhas. Ela vai se mover, mas não eternamente. Mesmo que haja espaço suficiente, ela vai parar em algum momento, né? De fato, isso acontece, mas não vai contra a primeira lei de Newton, pelo contrário: é a ação de forças - como a resistência do ar e o atrito com o chão - que obriga a cadeira a modificar seu movimento.

Se, de alguma forma, pudéssemos remover todo o ar ao redor e usar um chão perfeitamente liso, sem atrito, a cadeira se moveria indefinidamente, até que encontrasse um obstáculo. Forças não são necessárias para haver movimento, apenas para modificá-lo.

Consequências da primeira lei de Newton

Tudo que aprendemos nos leva a uma conclusão muito importante: se a força resultante externa sobre um corpo for nula, ele estará em repouso ou em movimento retilíneo uniforme.

Para entender isso, temos que lembrar que velocidade é uma grandeza vetorial: possui módulo, direção e sentido. Se o vetor velocidade não varia (seja em qualquer uma dessas características), então o corpo só pode estar em repouso ou em movimento retilíneo uniforme.

⚠️ Se um corpo está em repouso ou em movimento retilíneo uniforme, não quer dizer que não existem forças atuando sobre ele. Várias forças podem estar atuando sobre o corpo, desde que a soma vetorial seja nula.

Aplicações e exemplos da primeira lei de Newton

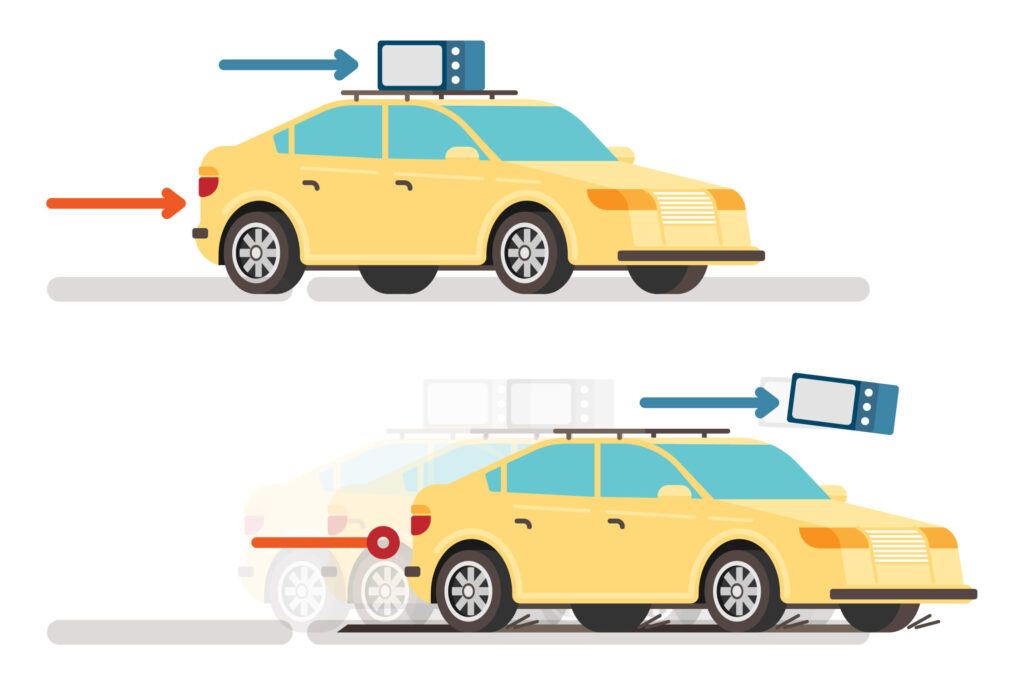
Se você já andou de ônibus, então sentiu na prática a primeira lei de Newton! Quando você está dentro de um veículo parado, por estar dentro dele, você também está parado. Se o ônibus começa a se mover para frente, então você, por inércia, tende a manter seu estado inicial de repouso. Por isso, sente como se fosse jogado para trás!

Da mesma forma, se você está dentro de um ônibus em movimento retilíneo uniforme e ele freia, você, por estar inicialmente em movimento retilíneo uniforme junto com o ônibus, vai tender a manter esse estado de movimento. Como consequência, sentirá como se fosse jogado para a frente.

Inércia

A primeira lei de Newton é conhecida também como lei da inércia. Inércia é a propriedade dos corpos de se opor a uma alteração no seu estado de movimento.

Se o corpo está em repouso, ele irá se opor a entrar em movimento. Por isso, precisamos de uma força para movê-lo. O mesmo se aplica para um corpo em movimento retilíneo e uniforme: ele irá se opor a mudar de velocidade ou parar. Assim, precisamos exercer uma força sobre ele para que isso aconteça.

É importante lembrar que a inércia varia de corpo para corpo, ou seja, alguns corpos resistem mais a uma alteração no seu movimento do que outros. Em outras palavras, corpos com mais massa possuem maior inércia.

É por isso que é mais fácil colocar em movimento (ou parar o movimento de) um corpo leve do que um corpo pesado. Portanto, podemos considerar a massa como a medida da inércia de um corpo.

👉 Leia também:

Como Star Wars ajuda a entender a velocidade da luz?

Gato de Schrödinger: vivo ou morto?

Segunda lei de Newton

A segunda lei de Newton, também conhecida como lei fundamental da dinâmica (tamanha sua importância!) relaciona a força resultante que atua sobre um corpo e a aceleração que ele adquire. Essa lei é representada matematicamente pela seguinte fórmula:

\[ \overrightarrow{F}_R = m \cdot \overrightarrow a \]

O que essa equação diz é que a força resultante sobre um corpo é igual ao produto da massa desse corpo pela aceleração que ele adquire devido à ação da força resultante.

Um detalhe que você precisa tomar cuidado é: essa força é a força resultante, ou seja, a soma vetorial de todas as forças que atuam sobre o corpo.

💡 Uma dica é desenhar um diagrama de forças para analisar as forças que atuam sobre o corpo, determinar a resultante e então aplicar a segunda das leis de Newton.

Aplicações e exemplos da segunda lei de Newton

De acordo com a segunda lei de Newton, se a força resultante for nula, a aceleração também será nula, ou seja, o corpo estará em repouso ou em movimento retilíneo uniforme. Assim, podemos chegar a conclusões importantes:

• a aceleração que um corpo adquire tem sempre a mesma direção e o mesmo sentido da força resultante que atua sobre ele. Afinal, um vetor multiplicado por um número positivo (massa é sempre positiva) resulta em um vetor com mesma direção e mesmo sentido.
• quanto maior a força resultante sobre um mesmo corpo, maior a aceleração adquirida por ele (para um valor constante de massa, força resultante e aceleração são diretamente proporcionais).
• para uma mesma força resultante, quanto maior a massa do corpo, menor a aceleração adquirida por ele (para um valor constante de força resultante, massa e aceleração são inversamente proporcionais).
• a massa é a medida da inércia de um corpo. Quanto maior for a massa de um corpo, mais difícil será alterar seu estado de movimento.

Para exemplificar a segunda lei de Newton, observe a figura abaixo:

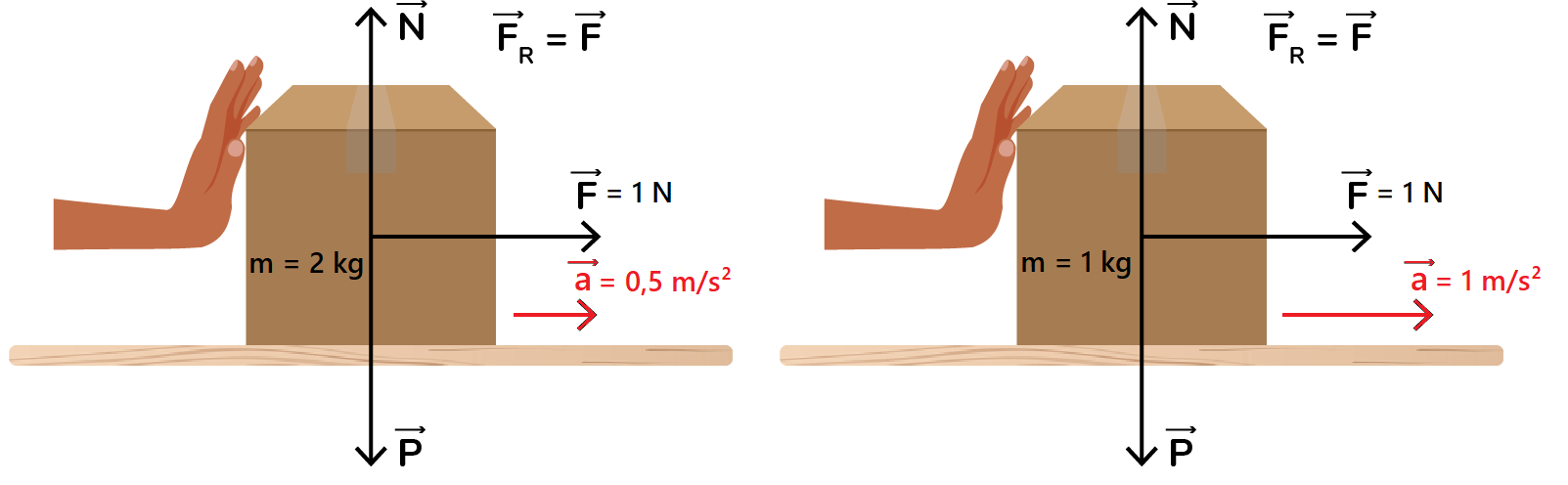
Na figura da esquerda, uma pessoa exerce uma força de módulo F = 1 N sobre uma caixa de massa m = 2 kg. Na vertical, as únicas forças que atuam sobre a caixa são seu peso e a força normal do chão, que se anulam. Como estamos desconsiderando forças como o atrito e a resistência do ar, a força resultante é a força F que a pessoa exerce.

Usando a segunda lei de Newton (F_R = m · a), podemos descobrir a aceleração que a caixa adquire:

\[ 1 = 2 \cdot a \\ a = \dfrac{1}{2} \\ a=0,5 m/s^{2} \]

Já na direita, a massa da caixa caiu pela metade, mas a força que a pessoa exerce continua a mesma. Assim, a nova aceleração da caixa é:

\[ 1 = 1 \cdot a \\ a = 1\ m/s^2 \]

Reduzindo a massa à metade, a aceleração dobra! Isso para uma força constante, o que demonstra a última conclusão que chegamos. Ou seja, quanto maior for a massa de um corpo, mais difícil será alterar seu estado de movimento.

Segunda lei de Newton e o teorema do impulso

Originalmente, no livro Princípios matemáticos da filosofia natural, Newton não representou a segunda lei dessa forma, e sim a partir da variação da quantidade de movimento. O teorema do impulso tem o mesmo significado da segunda lei de Newton, apenas representado com uma outra cara. Quer ver?

O teorema do impulso nos diz que o impulso da força resultante sobre um corpo é igual à variação da quantidade de movimento desse corpo:

\[ I = \Delta Q \]

A quantidade de movimento é dada por Q = m · v. Se considerarmos que a massa do corpo é constante, podemos reescrever a equação acima assim:

\[ I = m \cdot \Delta v \]

Lembra da definição do impulso de uma força? I = F · Δt. Logo:

\[ F_R \cdot \Delta t = m \cdot \Delta v \]

Dividindo os dois lados da equação por Δt:

\[ F_R = \dfrac{(m \cdot \Delta v)}{\Delta t} \]

Só que Δv/Δt é aceleração! Portanto, a equação acima vira:

\[ F_R = m \cdot a \]

Viu só? A partir do teorema do impulso, chegamos à fórmula da segunda lei de Newton! Ambas as equações nos dizem a mesma coisa: a velocidade de um corpo (pensando como um vetor, considerando módulo, direção e sentido) só muda se houver aceleração, ou seja, se atuar uma força resultante sobre esse corpo.

Terceira lei de Newton

Por último, a terceira lei de Newton, também chamada de lei da ação e reação, nos diz o seguinte:

"Para toda ação há sempre uma reação de mesmo módulo, mesma direção e sentido contrário"

“Ação” e “reação” são forças. Nesse sentido, forças sempre existem aos pares: você não pode pressionar uma parede sem que a parede pressione você de volta.

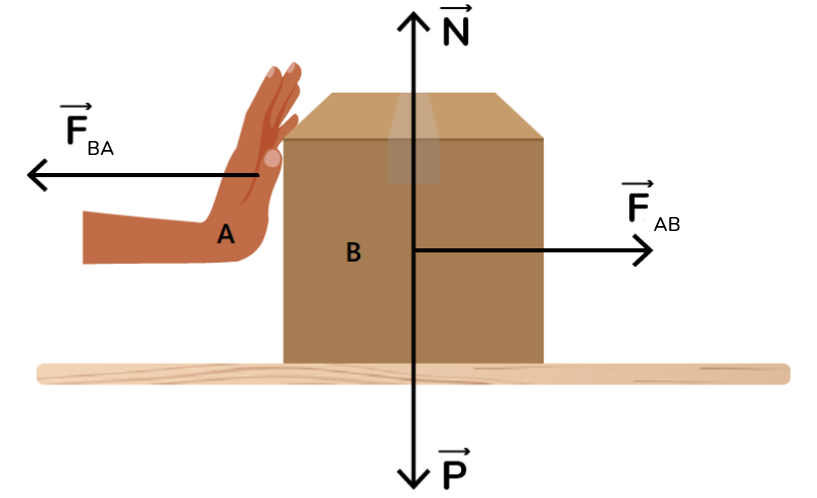
Isso significa que, sempre que um corpo A exerce uma força sobre um corpo B, o corpo B também exerce uma força sobre o corpo A, e essa força tem a mesma intensidade, mesma direção e sentido contrário ao da força exercida por A. As forças exercidas pelos corpos A e B formam o que chamamos de par ação-reação.

Consequências da terceira lei de Newton

Primeiramente, precisamos destacar o seguinte: quando dizemos que duas ou mais forças se anulam, essas forças devem, obrigatoriamente, atuar sobre um mesmo corpo.

Lembra dos exemplos da segunda lei de Newton? Lá, vimos que a normal e o peso se anulam. Isso só é possível porque ambas as forças atuam sobre o mesmo corpo, que é a caixa. Esse é um fato importantíssimo para entendermos as leis de Newton. A partir disso, vamos a algumas consequências da terceira lei:

• As forças de um par ação-reação envolvem apenas dois corpos, que exercem força um sobre o outro.
• Cada uma das forças de um par ação-reação atua sobre cada um dos corpos, então as forças de um par ação-reação nunca se anulam.

É um erro muito comum achar que peso e normal constituem um par ação-reação. Vamos entender melhor por que isso não é verdade?

Par ação-reação

Imagine uma bola de futebol em repouso sobre uma mesa horizontal. As únicas forças que atuam sobre a bola são seu próprio peso (que aponta para baixo na direção vertical) e a força normal da mesa sobre ela (que aponta para cima na direção vertical). Não há forças atuando sobre a bola na direção horizontal.

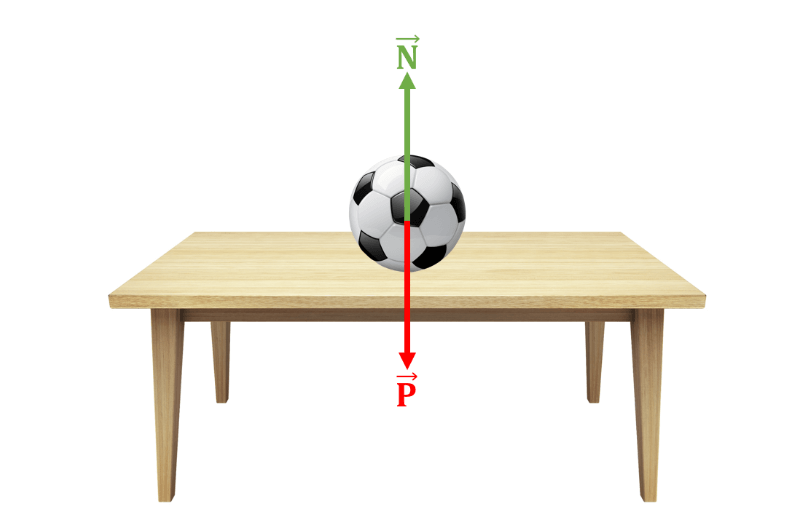
Como a bola está em repouso, a força resultante sobre ela deve ser nula. Isso significa que a soma vetorial do peso e da normal deve ser nula e, portanto, podemos escrever que P = N (peso e normal são, em módulo, iguais).

Aqui, já podemos destacar um erro comum: o de que peso e normal sempre serão iguais em módulo.

Isso não é verdade! Se inclinarmos a mesa, por exemplo, o peso vai continuar apontando para baixo na direção vertical, mas a normal inclinará junto com a mesa, já que ela é sempre perpendicular à superfície. Com isso, além de não terem a mesma direção, as forças não terão o mesmo módulo.

Voltando ao nosso exemplo: veja que peso e normal têm mesmo módulo, mesma direção e sentidos opostos. Essas são características de um par ação-reação, mas peso e normal não constituem um par ação-reação! Eu sei, isso pode parecer estranho, mas prometo que fará mais sentido. 🙏

Sabemos que, para duas forças formarem um par ação-reação, elas devem atuar em corpos diferentes. Aqui, peso e normal não são um par ação-reação, pois as duas atuam sobre a bola de futebol! Mas então quais são as outras forças dos pares?

Uma força normal é uma força de contato entre duas superfícies. Ela recebe esse nome porque é perpendicular/normal (forma 90º) às superfícies. Se a mesa faz uma força normal para cima sobre a bola, a bola faz uma força normal para baixo sobre a mesa! Já temos um par ação-reação.

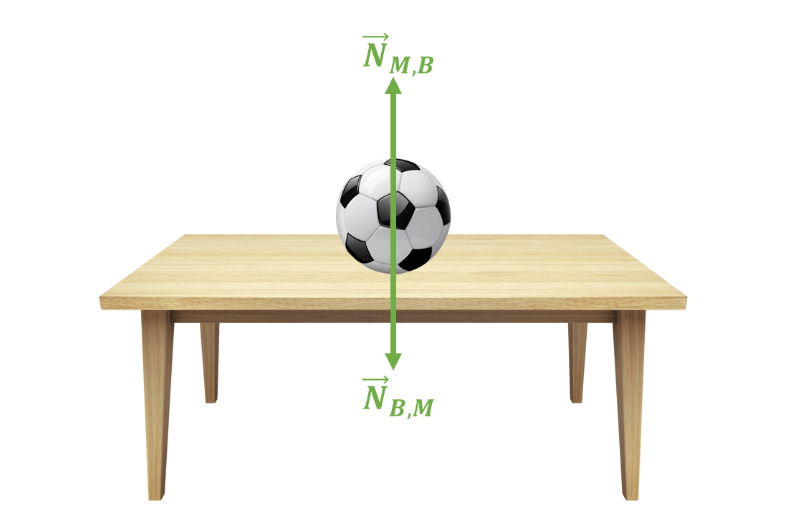
As forças \( \overrightarrow{N} _ {M,B} \) e \( \overrightarrow{N} _ {B,M} \) atuam sobre corpos diferentes (a bola e a mesa, respectivamente), então jamais podem se anular. Nesse caso, o módulo de ambas é igual ao módulo do peso, já que o sistema todo está em equilíbrio. Ok, mas e o peso?

Vamos pensar: só existem dois corpos envolvidos nas forças de um par ação-reação. Se o peso de um corpo é uma força exercida sobre o corpo pela Terra, a outra força será exercida sobre a Terra pelo corpo!

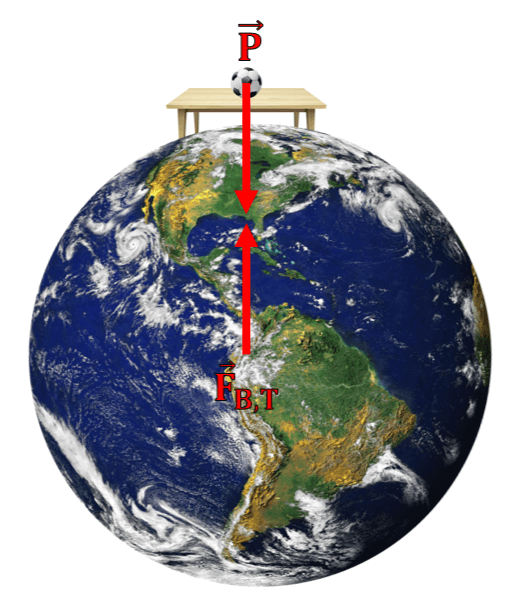
É isso mesmo: a bola também atrai a Terra. Logicamente, como a massa da Terra é muito maior do que a da bola, a aceleração sofrida pela Terra é perfeitamente desprezível.

Aplicações e exemplos da terceira lei de Newton

Alguns exemplos onde podemos observar a terceira das leis de Newton são quando:

• para decolar, um helicóptero utiliza suas hélices para empurrar o ar para baixo. Como consequência, o ar empurra as hélices para cima.;
• um foguete consegue decolar porque a queima de combustíveis propelentes expele gases para baixo, que, por sua vez, propulsionam o foguete para cima;
• durante a natação, uma pessoa empurra a água para trás com os braços e as pernas. A água, portanto, empurra a pessoa para frente.

Perceba que, em cada caso, citamos dois corpos (helicóptero e ar, foguete e gases, pessoa e água), sendo que cada corpo sofre ação da força exercida pelo outro. O par de forças de cada caso configura um par ação-reação.

👉 Leia também:

O que é termologia e como ela está presente no dia a dia?

Como a Física explica por que o céu é azul?

Fórmulas das leis de Newton

Tecnicamente, a segunda lei é a única das leis de Newton que possui o que podemos chamar de fórmula. No entanto, as outras duas leis podem ser representadas matematicamente. Vamos conferir cada uma delas.

Primeira lei de Newton

Matematicamente, podemos resumi-la através da seguinte representação:

\[ \overrightarrow{F} _R = \overrightarrow{0} \Longleftrightarrow \overrightarrow{v} = constante \]

Isso significa que, se a força resultante for nula, então a velocidade (como um vetor!) é constante, podendo ser nula (repouso) ou não (movimento retilíneo uniforme).

O contrário também é válido: se a velocidade é constante, ou seja, se um corpo está em repouso ou em movimento retilíneo uniforme, então sabemos que a força resultante sobre ele é nula.

Segunda lei de Newton

Como vimos, a lei fundamental da dinâmica pode ser representada pela seguinte fórmula:

\[ \overrightarrow F _R = m \cdot \overrightarrow {a} \]

Em que \( \overrightarrow F_{R} \) é a força resultante sobre um corpo, m é a sua massa e \( \overrightarrow a \) é a aceleração que ele adquire.

Terceira lei de Newton

Exploramos muitos detalhes sobre o significado dessa lei, mas ela pode ser representada de um jeito bem resumido:

\[ \overrightarrow F _{AB} = - \overrightarrow F _{BA} \]

Em outras palavras, o vetor força \( \overrightarrow F _{B,A} \) de um corpo B sobre um corpo A é o oposto do vetor força \( \overrightarrow F_{A,B} \) de um corpo A sobre um corpo B. O sinal negativo indica que um vetor é o oposto do outro, ou seja, eles têm mesmo módulo e mesma direção, mas sentidos contrários.

Outra forma de representar isso é dizendo que seus módulos são iguais:

\[ | \overrightarrow F _{A,B} | = | \overrightarrow F _{B,A} | \]

Resumo: leis de Newton

Agora que você já está fera nas leis de Newton, vamos relembrar o que aprendemos de mais importante sobre cada lei?

• Segundo a primeira lei de Newton, todo corpo tende a permanecer em seu estado de movimento, seja ele movimento retilíneo uniforme ou repouso, a não ser que uma força resultante externa o obrigue a modificar seu movimento.
• Se a força resultante sobre um corpo for nula, ele estará em repouso ou em movimento retilíneo uniforme.
• De acordo com a segunda das leis de Newton, a força resultante sobre um corpo é igual ao produto da massa desse corpo pela aceleração que ele adquire, ou seja, \[ \overrightarrow F _R = m \cdot \overrightarrow a \]

• Os vetores força resultante e aceleração têm mesma direção e mesmo sentido.
• Para uma mesma massa, força resultante e aceleração são diretamente proporcionais.
• Para uma mesma força resultante, massa e aceleração são inversamente proporcionais.
• A terceira lei de Newton descreve que, para toda ação, há sempre uma reação de mesmo módulo, mesma direção e sentido contrário.
• As forças de um par ação-reação nunca se anulam, pois atuam sobre corpos diferentes.

Como as leis de Newton caem no Enem e nos vestibulares

Vamos conferir agora três exemplos de questões sobre as leis de Newton: uma da Fuvest, uma da UFRGS e uma do Enem.

Exemplo 1

(Fuvest 2021)  Considere as seguintes afirmações:

I. Uma pessoa em um trampolim é lançada para o alto. No ponto mais alto de sua trajetória, sua aceleração será nula, o que dá a sensação de “gravidade zero”.

II. A resultante das forças agindo sobre um carro andando em uma estrada em linha reta a uma velocidade constante tem módulo diferente de zero.

III. As forças peso e normal atuando sobre um livro em repouso em cima de uma mesa horizontal formam um par ação-reação.

De acordo com as leis de Newton:

1. Somente as afirmações I e II são corretas.
2. Somente as afirmações I e III são corretas.
3. Somente as afirmações II e III são corretas.
4. Todas as afirmações são corretas.
5. Nenhuma das afirmações é correta.

Resposta: [E]
I - Incorreta: em um lançamento vertical, se desprezarmos a resistência do ar, a aceleração é a aceleração gravitacional. No ponto mais alto, a velocidade é nula, mas a aceleração não: ela é constante.

Podemos, inclusive, relacionar isso com a segunda lei de Newton: como desprezamos a resistência do ar, a força resultante após o lançamento será o próprio peso da pessoa. Como \( F_R = m \cdot a = P = m \cdot g \), concluímos que \( a = g \) (pois podemos simplificar as massas).

II - Incorreta: como o movimento é retilíneo e uniforme, a resultante das forças agindo sobre o carro é nula, de acordo com a primeira lei de Newton.

III - Incorreta: o peso e a normal atuam sobre o mesmo corpo, que é o livro, então não formam um par ação-reação. Além disso, essas forças se anulam, o que nunca ocorre com as forças de um par ação-reação.

Exemplo 2

(UFRGS 2017) Aplica-se uma força de 20 N a um corpo de massa m. O corpo desloca-se em linha reta com velocidade que aumenta 10 m/s a cada 2 s. Qual o valor, em kg, da massa m?

a) 5

b) 4

c) 3

d) 2

e) 1

Resposta: [B]
A velocidade aumenta 10 m/s a cada 2 s, ou seja, para um intervalo Δt = 2 s, a variação da velocidade vale Δv = 10 m/s. Calculando a aceleração:

\[ a = \dfrac{\Delta v}{\Delta t} \\ a = \dfrac{10}{2} \\ a = 5\ m/s^2 \]

Como a força aplicada vale 20 N, podemos usar a segunda lei de Newton para calcular a massa do corpo:
\[ F_R = m \cdot a \\ 20 = m \cdot 5 \\ m = \dfrac{20}{5} \\ m = 4\ kg \]

Exemplo 3

(Enem PPL 2012) Durante uma faxina, a mãe pediu que o filho a ajudasse, deslocando um móvel para mudá-lo de lugar. Para escapar da tarefa, o filho disse ter aprendido na escola que não poderia puxar o móvel, pois a terceira lei de Newton define que se puxar o móvel, o móvel o puxará igualmente de volta, e assim não conseguirá exercer uma força que possa colocá-lo em movimento.

Qual argumento a mãe utilizará para apontar o erro de interpretação do garoto?

a) A força de ação é aquela exercida pelo garoto.

b) A força resultante sobre o móvel é sempre nula.

c) As forças que o chão exerce sobre o garoto se anulam.

d) A força de ação é um pouco maior que a força de reação.

e) O par de forças de ação e reação não atua em um mesmo corpo.

Resposta: [E]
De fato, o menino puxa o móvel e o móvel o “puxa” com mesma intensidade e mesma direção, mas sentido oposto. No entanto, por essas duas forças atuarem sobre corpos diferentes, elas nunca se anulam, de modo que ele consegue colocar o móvel em movimento.

🥇 Quer preparação máxima para ter alto rendimento no Enem e ingressar no curso dos seus sonhos? 
Então conheça a plataforma do Aprova Total!