Lei da Gravitação Universal: veja conceitos e fórmulas

Em algum momento da vida, você provavelmente se perguntou por que as coisas caem para baixo. É possível que alguém tenha te falado que "é por causa da gravidade". Muita gente sabe que as coisas caem "por causa da gravidade", mas será que essas pessoas sabem como isso acontece? A essência disso está na Lei da Gravitação Universal de Newton.

Nesse post, você vai conhecer e entender a Lei da Gravitação Universal, que explica desde coisas mais simples, como objetos caindo, até planetas orbitando o Sol! Além disso, você verá exemplos de aplicações dessa lei, com foco em como ela costuma cair nos vestibulares e no Enem.

A Lei da Gravitação Universal

Nos anos 1665 e 1666, uma epidemia de peste tomou conta da Inglaterra, o que obrigou o jovem Isaac Newton a ficar de quarentena em sua fazenda. Durante esse tempo, Newton fez muitas descobertas importantes para a física e para a matemática, como a Lei da Gravitação Universal. Essa lei é o "coração" de uma das áreas mais antigas da física: a Gravitação Universal, que é uma área intimamente ligada, sobretudo, à astronomia.

A ideia é que, se considerarmos dois corpos que possuem massa, um vai exercer sobre o outro uma força. Essa força é chamada de força gravitacional e, quanto maiores forem as massas dos corpos, mais intensa será essa força. Além disso, quanto mais próximos os corpos estiverem, mais intensa será essa força que um exerce sobre o outro.

A força gravitacional tem relação com aquela famosa lenda que diz que a queda de uma maçã teria sido o gatilho para Newton conceber a ideia da Gravitação Universal. No entanto, ninguém comprovou de fato essa história.

Cálculo da força gravitacional

E como podemos calcular a força gravitacional? O valor da força gravitacional F_G, que um corpo exerce sobre outro, pode ser calculado pela seguinte equação:

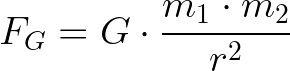
Nesse caso, m₁ e m₂ são os valores das massas dos corpos e r é a distância entre os seus centros. G é uma constante conhecida como constante gravitacional. Qual é o valor da constante gravitacional? No Sistema Internacional:

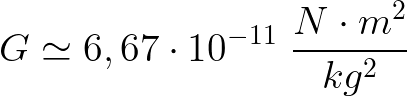
Se você já estudou força elétrica, poderá reparar que a expressão da Lei da Gravitação Universal se parece muito com a expressão da Lei de Coulomb. Elas são realmente muito parecidas. No entanto, enquanto a força elétrica pode ser tanto de atração quanto de repulsão, a força gravitacional é sempre de atração. Em outras palavras, dois corpos com massa nunca irão sofrer uma força de repulsão gravitacional.

A força gravitacional e a terceira lei de Newton

Primeiramente, é importante esclarecer uma coisa: a força gravitacional que um corpo A exerce sobre um corpo B é igual, em módulo, à força que o corpo B exerce sobre o corpo A. Assim, basta calcularmos uma vez o módulo da força gravitacional e, consequentemente, saberemos o valor dessas duas forças.

Também é importante notar que essas duas forças formam um par ação-reação: elas são iguais em módulo e em direção, mas têm sentidos opostos. Isso significa que a força gravitacional é um exemplo prático da terceira lei de Newton.

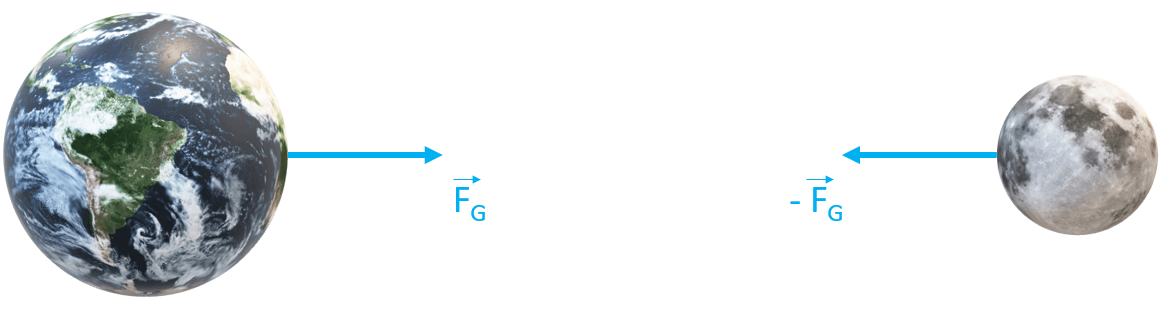
Na imagem acima, podemos ver, através dos vetores que representam as forças que a Terra e a Lua sentem em decorrência uma da outra, que as forças gravitacionais têm o mesmo módulo, a mesma direção, mas sentidos contrários.

Quais corpos sofrem atração gravitacional?

Tá, mas então, só os planetas e outros corpos enormes sofrem atração gravitacional?

Não! Todo corpo com massa sofre atração gravitacional de um outro corpo com massa, não importa se ele é uma bolinha de tênis de mesa ou uma estrela imensa!

Por quê, então, eu não atraio os objetos ao meu redor?

Bom, na verdade, você atrai! Entretanto, a sua massa e a dos objetos que estão perto de você são muito pequenas! Principalmente se considerarmos o valor da constante G, que é realmente muito pequena. Sendo assim, a força gravitacional entre você e os objetos do seu cotidiano não é forte o suficiente para superar o efeito de forças dissipativas presentes, tais como o atrito.

Corpos celestes, como planetas, luas e estrelas, são corpos muito massivos. Por conta disso, a força gravitacional que eles exercem é muito grande. Isso faz com que os efeitos causados por eles sejam mais perceptíveis. Os planetas orbitando o Sol, a Lua orbitando a Terra, as marés influenciadas pela Lua e o nosso próprio peso são consequências da atração gravitacional que corpos celestes muito grandes exercem.

O que é a força peso?

Quando estudamos Dinâmica, uma das primeiras forças que aprendemos a calcular é a força peso. Para isso, usamos aquela velha fórmula P = m . g, em que m é a massa do objeto e g é a aceleração gravitacional, cujo valor é de aproximadamente 10 m/s².

No geral, podemos considerar que o peso de um objeto em um planeta (ou algum outro corpo celeste bem grande, como uma lua) é igual à força gravitacional que esse planeta exerce sobre o objeto. Então, podemos utilizar também a Lei da Gravitação Universal para calcular esse peso. Nesse caso, devemos usar a massa do objeto e a massa do planeta no cálculo. Na Lua, por exemplo, o seu peso seria menor do que aqui na Terra, já que a Lua tem massa menor do que a Terra.

Mas por que eu iria querer usar aquela fórmula complicada para calcular o peso de um objeto? Eu posso simplesmente usar a velha fórmula do peso!

Isso é verdade! Se você souber a massa do objeto e a aceleração gravitacional no planeta, é mais fácil calcular o peso pela fórmula da Dinâmica. No entanto, a relação de igualdade entre a força peso e a força gravitacional nos dá algumas vantagens. Vamos ver uma delas a seguir!

Aceleração gravitacional

Sabemos que o valor da aceleração gravitacional g é de cerca de 10 m/s² na superfície da Terra. Às vezes, usamos o valor 9,8 m/s²_. Mas e se quiséssemos calcular o valor de g em um lugar muito alto, como na órbita de um satélite? Ou então calcular a aceleração gravitacional na superfície de um outro planeta? Essas coisas já apareceram em alguns vestibulares.

Para isso, devemos igualar as duas equações: do peso de um objeto e da força gravitacional entre esse objeto e o planeta onde ele está.

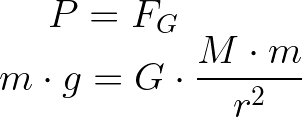
Perceba que, ao invés de chamar as massas de m₁ e de m₂, chamamos de m (massa do objeto) e de M (massa do planeta). Podemos isolar g na equação ao dividir os dois lados por m:

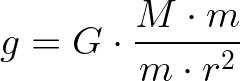
Veja que temos m no numerador e no denominador, então podemos simplificar:

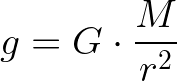
Essa é a expressão geral para calcularmos uma aceleração gravitacional. Podemos perceber que a aceleração gravitacional só depende da massa M do planeta (ou do corpo celeste analisado) e da distância r ao centro desse corpo. Veja que a aceleração gravitacional não depende da massa m do objeto que está sob efeito dessa aceleração.

Atenção: a distância r não é a distância entre ponto que estamos analisando e a superfície do corpo celeste. É a distância do ponto que estamos analisando até o centro do corpo celeste.

Campo gravitacional

Ao redor do planeta Terra, por exemplo, todos os corpos sentem uma atração gravitacional que aponta para o centro da Terra. Isso se deve ao campo gravitacional, uma grandeza que é uma "influência" que os corpos que possuem massa exercem sobre o espaço ao seu redor.

Nós possuímos o nosso campo gravitacional. Basicamente, tudo que tem massa possui. Entretanto, ele só passa a ser considerável se a massa for muito grande, como acontece com os corpos celestes.

A teoria por trás do campo gravitacional dos corpos celestes explica que, quanto mais massivo for o corpo, mais esférico ele tende a ser (NÃO, A TERRA NÃO É PLANA!). E, a cada ponto ao redor do corpo, o campo aponta sempre para o centro dele. É por isso que as pessoas na China (ou em algum lugar do outro lado do planeta) também são atraídas para o centro da Terra e não "caem", como você pode ter imaginado quando era criança.

Satélites e a Lei da Gravitação Universal

Hoje em dia, é difícil imaginar o que seria da gente se não fossem os satélites. Afinal, eles nos proporcionam sinal de internet, GPS, ajudam a realizar previsões meteorológicas... Mas esses são os satélites artificiais. Existem também os satélites naturais, como a nossa Lua. No geral, satélites são corpos que orbitam um planeta.

Satélites também costumam aparecer em questões de Gravitação Universal nos vestibulares, inclusive na prova do Enem. A ideia para resolver essa questão era lembrar que, quanto mais próximo um corpo estiver do centro da Terra, maior será a força gravitacional que a Terra exerce sobre ele.

Você pode se perguntar: como os satélites conseguem orbitar a Terra sem "cair" para o chão?

A verdade é que eles estão sempre caindo! Enquanto um satélite está em órbita, ele está em uma queda constante. Mas ele não atinge o chão porque ele também está se movendo muito rapidamente "para fora" da Terra.

Graças à força gravitacional, eles não seguem adiante para fora do planeta. E, por conta de sua velocidade alta (com a qual são lançados), eles não colidem contra a superfície, mas acompanham a curvatura da Terra.

Órbitas

Pelas leis de Kepler, sabemos que as órbitas de planetas em torno do Sol e de satélites em torno de um planeta são elípticas, ou seja, têm a forma de um elipse. Todavia, algumas situações nos permitem aproximar a órbita como se ela fosse circular.

É muito comum encontrarmos exercícios que pedem que consideremos circular a órbita de um planeta ou satélite. Isso é ótimo! Afinal, trabalhar com elipses costuma ser complicado. Órbitas circulares são mais simples, além de nos permitirem usar conceitos e ferramentas de movimentos circulares.

Por exemplo: em muitos casos, nós podemos considerar que a força resultante sobre um objeto em órbita é simplesmente a força gravitacional e que esse objeto orbita em um movimento circular. Isso te lembra alguma coisa? Se você pensou em força centrípeta, tem toda a razão!

Se considerarmos a órbita circular, a força gravitacional que o corpo celeste exerce sobre o objeto em órbita é a própria força centrípeta.

Satélites geoestacionários

Um tipo específico de satélite que costuma dar as caras nos vestibulares é o satélite geoestacionário, que recebe esse nome porque orbita a Terra estando sempre acima do mesmo lugar. Uma outra forma de dizer isso é que ele acompanha a rotação da Terra.

Curiosidade: como os satélites geoestacionários acompanham a rotação da Terra, seu período de órbita é de 24 horas, que é o tempo aproximado que a Terra leva para realizar uma volta ao redor de si mesma.

Gostou de aprender mais sobre a Gravitação Universal? Agora você vai conseguir explicar melhor para as pessoas por que as coisas caem ao invés de falar apenas que é por causa da gravidade!

Quer saber mais sobre as Leis de Newton que caem no Enem e vestibulares? Na plataforma do Aprova Total você encontra milhares de opções. Se você ainda não é aluno, inscreva-se já!