Trigonometria: conceitos e principais fórmulas

A trigonometria é uma área da Matemática na qual a geometria e a álgebra se relacionam para o desenvolvimento de diversos estudos dos lados e ângulos do polígono mais simples: o triângulo. Além disso, com ela, podemos aprofundar os conhecimentos tanto da geometria plana quanto da espacial. Confira todos os conceitos e as principais fórmulas!

Trigonometria no triângulo retângulo

O principal estudo da trigonometria está baseado sobre os triângulos retângulos. Através desse tipo de triângulo, estabelecemos as principais razões trigonométricas: seno, cosseno e tangente. Como vimos estudamos em nosso texto sobre geometria plana, o triângulo retângulo é aquele que possui um ângulo de 90º, ou seja, um ângulo reto. Por isso o nome triângulo retângulo. Como em cada triângulo, os maiores lados estão opostos aos maiores ângulos, e no triângulo retângulo o maior ângulo de qualquer triângulo desse tipo é o de 90º, o lado oposto a ele será chamado de Hipotenusa, enquanto os demais lados, que formam o ângulo reto, são chamados de catetos. Mais adiante, quando estivermos preocupados com os ângulos agudos (por consequência do ângulo reto ser o maior ângulo desse tipo de triângulo), iremos chamá-los de cateto oposto e cateto adjacente.

No triângulo retângulo acima, os lados \( b \) e \( c \) são definidos como catetos e, o lado \( a \), a hipotenusa.

Razões trigonométricas no triângulo retângulo

Por definição, uma razão é uma divisão entre duas grandezas (que você pode revisar no nosso post de razão e proporção). Dessa forma, razões trigonométricas são divisões entre medidas do triângulo retângulo que irão definir nossas medidas trigonométricas ( \( sen, cos, tg \) ). Dessa forma, para entendermos as três razões, usaremos o ângulo \( \alpha \) , do triângulo retângulo da primeira imagem, como referência. Como mencionamos anteriormente, quando temos um ângulo de referência, nossos catetos ganham "sobrenome" e passam a ser chamados de cateto oposto, quando o cateto for oposto ao ângulo \( \alpha \) e cateto adjacente, quando o cateto estiver sendo tocado pelo ângulo \( \alpha \). Nesse caso, os catetos opostos e adjacentes ao ângulo \( \alpha \) são, respectivamente, \( c \) e \( b \).

Seno

O seno é a razão trigonométrica que relaciona o cateto oposto com a hipotenusa, ou seja, em relação ao ângulo \( \alpha \) analisado, temos:

\[ sen \left( \alpha \right) = \dfrac{\text{cateto oposto (C.O.)}}{\text{hipotenusa (hip)}} \]

Cosseno

O cosseno, semelhante ao seno, é a razão que relaciona um cateto com a hipotenusa também, porém, desta vez o cateto é o adjacente. Portanto o cosseno é:

\[ cos \left( \alpha \right) = \dfrac{\text{cateto adjacente(C.A.)}}{\text{hipotenusa (hip)}} \]

Tangente

A tangente, diferentemente das outras duas razões diretas da trigonometria, é a razão que relaciona os dois catetos, sendo o oposto sobre o adjacente, dessa maneira:

\[ tg \left( \alpha \right) = \dfrac{\text{cateto oposto (C.O.)}}{\text{cateto adjacente (C.A.)}} \]

Além disso, ao dividirmos a razão seno pela razão cosseno, obtemos o mesmo resultado da tangente, isto é:

\[ tg \left( \alpha \right) = \dfrac{sen \left( \alpha \right)}{cos \left( \alpha \right)} \]

Para memorizar as razões trigonométricas há um macete conhecido como "SOHCAHTOA", em que a cada três letras significam uma razão da trigonometria. SOH remete ao S de seno, O de oposto e H de hipotenusa. Por outro lado, CAH lembra o C de cosseno, A de adjacente e H de hipotenusa. Por fim, o TOA refere ao T de tangente, O de oposto e A de adjacente.

• SOH: \( sen \left( \alpha \right) = \dfrac{\text{cateto oposto (C.O.)}}{\text{hipotenusa (hip)}} \)
• CAH: \( cos \left( \alpha \right) = \dfrac{\text{cateto adjacente(C.A.)}}{\text{hipotenusa (hip)}} \)
• TOA: \( tg \left( \alpha \right) = \dfrac{\text{cateto oposto (C.O.)}}{\text{cateto adjacente (C.A.)}} = \dfrac{sen \left( \alpha \right)}{cos \left( \alpha \right)} \)

Razões Inversas da Trigonometria

Acima, mostramos as razões trigonométricas do triângulo retângulo. Neste momento mostraremos as razões trigonométricas inversas, que nada mais são do que o inverso das razões da trigonometria, ou seja, o inverso do seno, cosseno e tangente.

Secante

A secante é a razão inversa do cosseno e, por isso, é definida por:

\[ sec \left( \alpha \right) = \dfrac{1}{cos \left( \alpha \right)} = \dfrac{\text{hip}}{\text{C.A.}} \]

Cossecante

A cossecante, de forma análoga, é o inverso da razão seno, dessa maneira:

\[ cossec \left( \alpha \right) = \dfrac{1}{sen \left( \alpha \right)} = \dfrac{\text{hip}}{\text{C.O.}} \]

Cotangente

Por fim, a cotangente, por consequência, é a razão inversa da tangente e é definida por:

\[ cotg \left( \alpha \right) = \dfrac{cos \left( \alpha \right)}{sen \left( \alpha \right)} = \dfrac{\text{C.A.}}{\text{C.O.}} \]

Relações métricas no triângulo retângulo

Quando estudamos os triângulos lá na geometria plana, vimos alguns resultados importantíssimos sobre relações entre as medidas do triângulo retângulo e a projeção da altura relativa à hipotenusa.O principal teorema trigonométrico abordado é o teorema de Pitágoras. Este teorema nos diz que em um triângulo retângulo, de hipotenusa a e catetos b e c, temos a seguinte relação:

a² = b² + c²

Além do teorema de Pitágoras, com a ajuda da semelhança de triângulos foram descobertas algumas relações métricas do triângulo retângulo. Para isso, veja o triângulo abaixo:

Com as medidas identificadas, podemos afirmar que são válidas as seguintes relações:

1. \( c^2 = a\cdot n \)
2. \(b^2 = a\cdot m \)
3. \(h^2 = m\cdot n \)
4. \(a\cdot h = b\cdot c \)

Trigonometria para qualquer triângulo

Até agora estudamos a trigonometria para os triângulos que possuem a característica de serem retângulos. A partir de agora, mostraremos algumas manipulações algébricas com a ajuda da trigonometria e da geometria plana que efetuaram a lei dos senos, cossenos e das áreas.

Lei dos senos

A lei dos senos é uma ferramenta utilizada para relacionar os lados e os ângulos de um triângulo qualquer. A principal ferramenta usada para determinar a lei dos senos é a manipulação geométrica do ângulo inscrito a circunferência. Não cabe a esse post explicitar os detalhes dessa manipulação, porém, para que você possa entender, acompanhe a imagem abaixo:

Acima, vemos o triângulo de lados \(a, b\) e \(c\) e ângulos \(\alpha, \beta\) e \(\gamma\) inscrito na circunferência de raio \(r\). Além disso, visualizamos a seguinte informação: o diâmetro da circunferência inscrita que passa pelo vértice do ângulo \( \beta \) determina um novo triângulo que mantém um ângulo igual a \( \alpha\) e um dos lados igual ao diâmetro da circunferência. Com a ajuda da geometria plana, identificamos que esse novo triângulo é retângulo em \( \gamma + \gamma_1 \), ou seja, a soma dos ângulos \(\gamma\) e \(\gamma_1\) é 90 graus. Sendo assim, notamos que o valor do diâmetro \(2R\) é a hipotenusa e através da razão seno, notamos a seguinte informação:

\[ sen \left( \alpha \right) = \dfrac{a}{2R} \Rightarrow \dfrac{a}{sen \left( \alpha \right)} = 2\cdot R \]

Repetindo esse processo para os ângulos \( \beta \) e \( \gamma\), obtemos a seguinte relação que define a lei dos senos.

\[ \dfrac{a}{sen \left( \alpha \right)} = \dfrac{b}{sen \left( \beta \right)} =\dfrac{c}{sen \left( \gamma \right)} = 2\cdot R \]

Lei dos cossenos

A lei dos cossenos é a ferramenta usada para determinar valores de um ângulo tendo todos os lados ou determinar o valor de um lado tendo os valores dos outros dois lados e do ângulo oposto a ele. Para isso, acompanhe a figura abaixo:

Para compreender a lei dos cossenos, basta, apenas, conhecer a trigonometria. Sendo assim, no triângulo qualquer de lados \(a, b\) e \(c\) e ângulos \(\alpha, \beta\) e \(\gamma\) acima, identificamos o segmento \(h\), altura referente ao lado \(c\), que origina outros dois triângulos retângulos. As duas primeiras informações que podemos identificar é aplicando o teorema de Pitágoras nos dois triângulos retângulos:

1. \( a^2 = h^2 + (c-x)^2 \Rightarrow a^2 = h^2 + c^2 -2\cdot c \cdot x + x^2 \)
2. \( b^2 = h^2 + x^2 \Rightarrow x^2 = b^2 - h^2 \)

Ao substituir a equação (2) em (1), obtemos a seguinte situação:

\[ \begin{eqnarray} a^2 &=& h^2 + c^2 - 2\cdot c \cdot x + b^2 -h^2 \\ a^2 &=& b^2 + c^2 -2 \cdot c \cdot x \end{eqnarray} \]

Nesse momento, obtemos o lado \(a\) em função dos outros lados e do valor \(x\). Entretanto, podemos aplicar o cosseno no triângulo retângulo de lado \(x\) e obter o seguinte resultado:

\[ cos \left( \alpha \right) = \dfrac{x}{b} \Rightarrow x = b \cdot cos \left( \alpha \right) \]

Portanto, unindo as duas últimas equações obtidas, obtemos a lei dos cossenos em relação ao lado a e seu ângulo oposto \(\alpha\):

\[ a^2 = b^2 + c^2 -2\cdot b \cdot c \cdot \cos \left( \alpha \right) \]

Temos até uma frase mnemônica para te ajudar a lembrar dessa fórmula

Pitágoras menos 2 b se cossa

\( a^2 = b^2 + c^2 -2 \cdot b \cdot c \cdot cos \left( \alpha \right) \)

Como você deve imaginar, podemos aplicar a relação acima para os demais lados e ângulos e, mantendo sempre isolado na igualdade o lado oposto ao ângulo, dessa forma, as leis dos cossenos são dadas por:

\[ \begin{eqnarray} a^2 &=& b^2 + c^2 -2 \cdot b \cdot c \cdot cos \left( \alpha \right) \\ b^2 &=& a^2 + c^2 -2 \cdot a \cdot c \cdot cos \left( \beta \right) \\ c^2 &=& a^2 + b^2 -2 \cdot a \cdot b \cdot cos \left( \gamma \right) \end{eqnarray} \]

Lei das áreas

A lei das áreas é a mais simples de identificar e, através da imagem anterior, podemos entendê-la com facilidade. Antes disso, devemos lembrar que a fórmula básica da área de um triângulo é:

\[ A = \dfrac{B \cdot H}{2} ]

Em que \(B\) é a base do triângulo e \(H\) é a altura relativa à base, sendo os dois segmentos, perpendiculares. Se tomarmos a base como o lado \(c\), notaremos que a altura é o segmento \(h\). Portanto, a área do triângulo é:

\[ A = \dfrac{c \cdot h}{2} \]

Perceba que, ainda, podemos substituir \(h\) em função do lado \(a\) ou do lado \(b\), aplicando as relações seno:

1. \( sen \left( \beta \right) = \dfrac{h}{a} \Rightarrow h = a \cdot sen \left( \beta \right) \)
2. \( sen \left( \alpha \right) = \dfrac{h}{b} \Rightarrow h = b \cdot sen \left( \alpha \right) \)

Logo, podemos substituir (i) ou (ii) na área do triângulo e obter:

3. \( A = \dfrac{c \cdot a \cdot sen \left( \beta \right)}{2} \)
4. \( A = \dfrac{c \cdot b \cdot sen \left( \alpha \right)}{2} \)

Além disso, se tomarmos outro lado como base do triângulo, obteremos também a seguinte relação:

5. \( A = \dfrac{a\cdot b \cdot sen \left( \gamma \right)}{2} \)

Portanto, a lei das áreas nos diz que a área de um triângulo é igual ao produto de dois lados adjacentes e o seno do ângulo formado por esses lados.

Ângulos na trigonometria

O ângulo é uma grandeza que mede a abertura entre duas semirretas. Suas principais unidades são graus (º) e radianos (\(rad\)) e ainda, a unidade do grau possui subunidades denotadas por minutos ('), que equivale a \( \dfrac{1}{60} \) do grau, e segundos (''), que equivale a \( \dfrac{1}{60} \) do minuto ou ainda \( \left( \dfrac{1}{60} \right)^2 \) do grau. Ja a medida em radianos, é determinada da seguinte forma: imagine uma circunferência de raio \(r\), agora essa medida \(r\) é calculada como um arco de circunferência e ligamos a outra extremidade ao centro, escrevendo outro raio (como se fosse um arco arco "equilátero"). A abertura de um raio determina \( 1 rad\), realizando uma conversão \(1rad = 57,296º \).

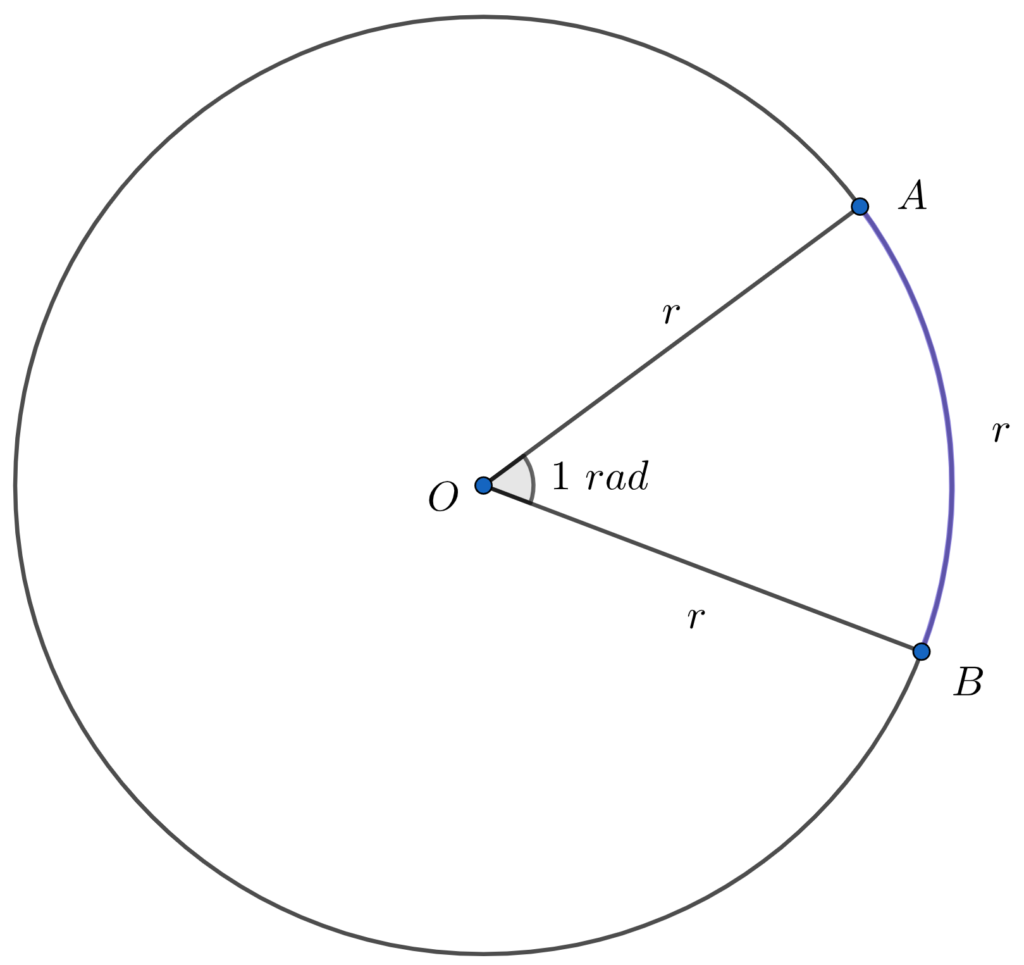
Temos que, uma volta completa equivale a \( 360º\) ou ainda ( 2\pi rad \), e para realizar a conversão de graus para radianos, podemos a seguinte regra de três

Tipos de ângulos

O ângulo raso é a metade de um ângulo completo, ou seja, 180º. Em consequência, o ângulo reto é a metade de um ângulo raso, isto é, 90º. Além disso, quando não há abertura dizemos que o ângulo é nulo, logo, 0º.

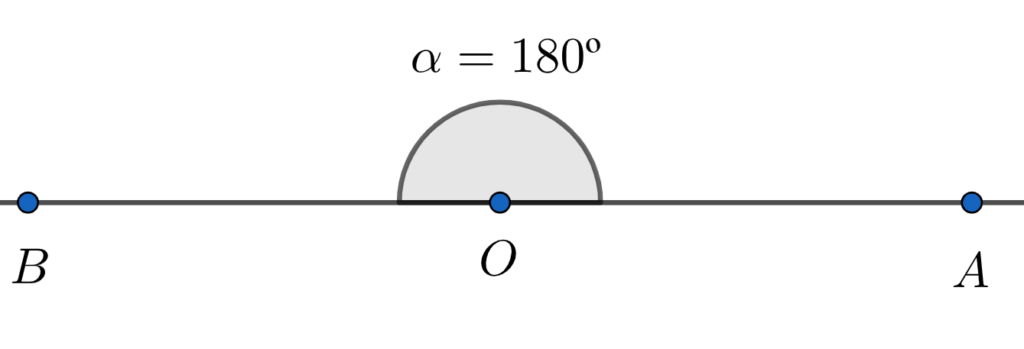
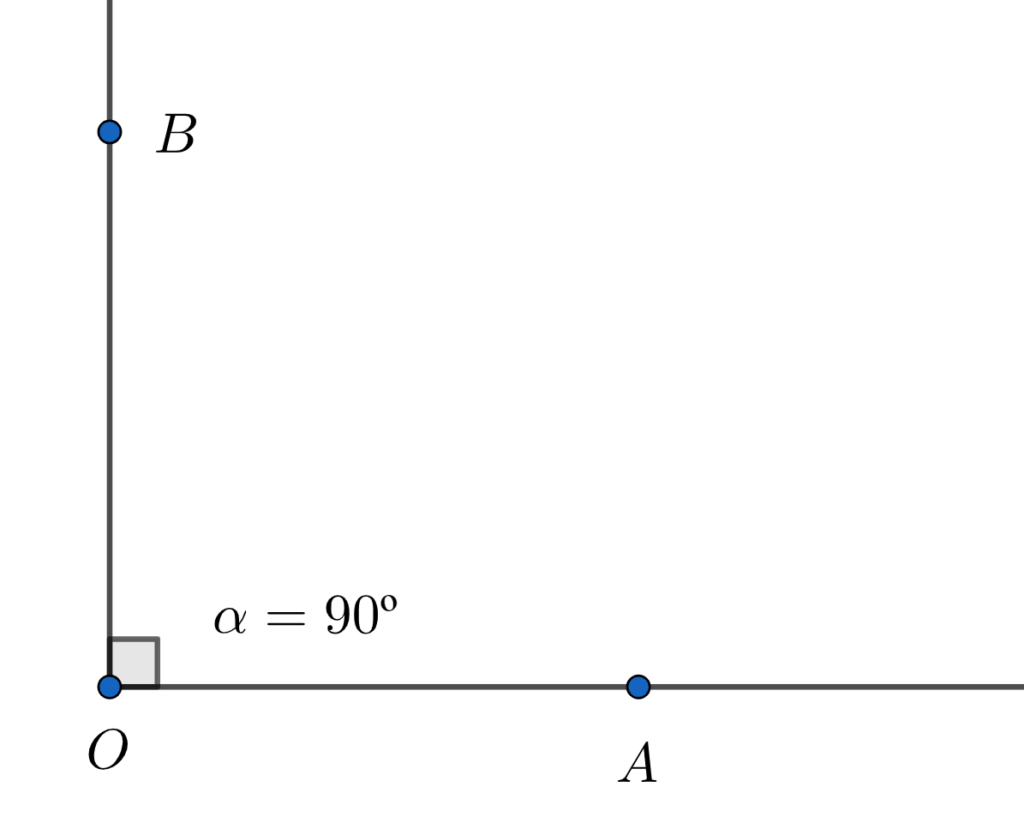
Entretanto, há ângulos que estão entre esses valores principais, por isso, dizemos que um ângulo é agudo, quando ele está entre 0º e 90º. Se for obtuso, é porque o ângulo está entre 90º e 180º. Por fim, se um ângulo estiver entre 180º e 360º, chamamos o de ângulo côncavo.

Radianos

Como comentamos anteriormente, o ângulo pode ser medido em radianos, vamos nos aprofundar um pouco mais no conhecimento dessa medida pois, apesar dela não ser tão intuitiva, é a mais utilizada em computadores, calculadoras e problemas.

Visualize uma circunferência de raio \( r\), agora imagine que podemos pegar essa medida, e curvar ela de forma que se encaixe perfeitamente na circunferência como na animação a baixo

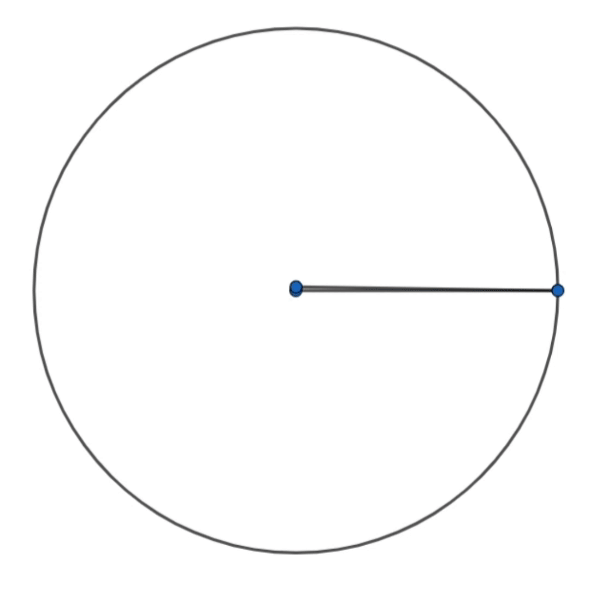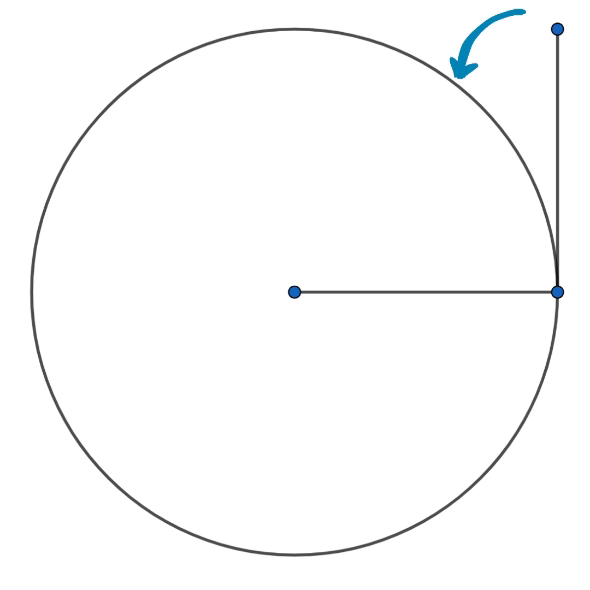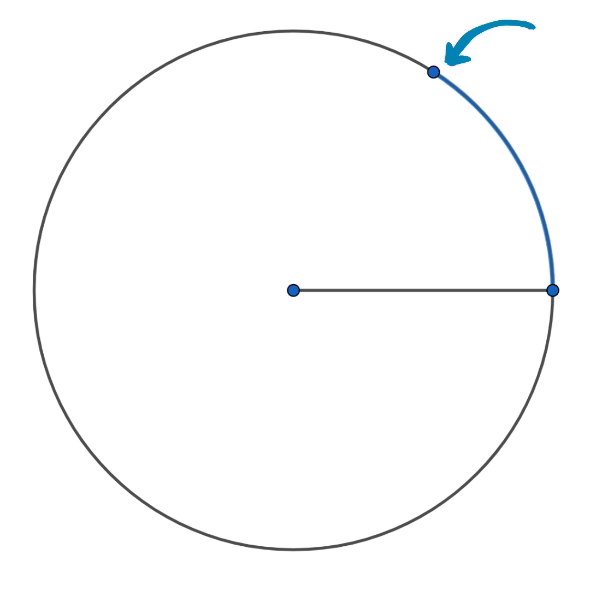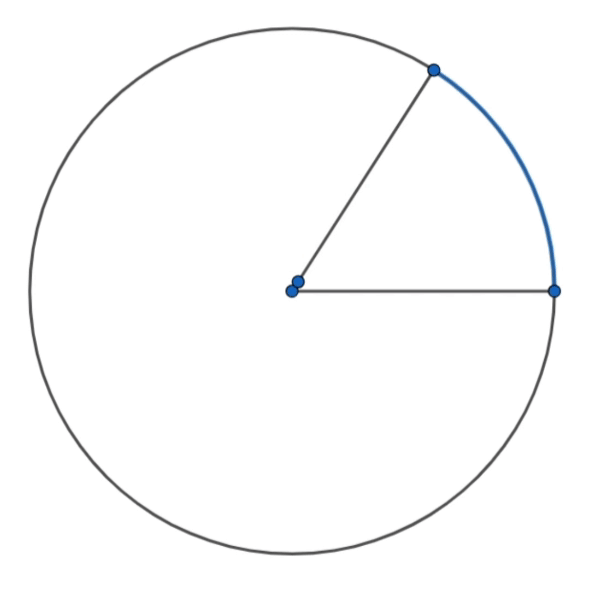
Observe que criamos uma bela "fatia de pizza", formalmente conhecida como setor circular, definida por dois segmentos de medida \(r\) e um comprimento de arco também de medida \(r\). Observe, que conseguimos encaixar nessa circunferência 6 medidas exatas de arcos com medida \(r\), só que sobra um pedacinho que tem medida aproxima \(0,28\cdot r\), ou seja, esse arco tem aproximadamente \(28\%\) a medida do raio.

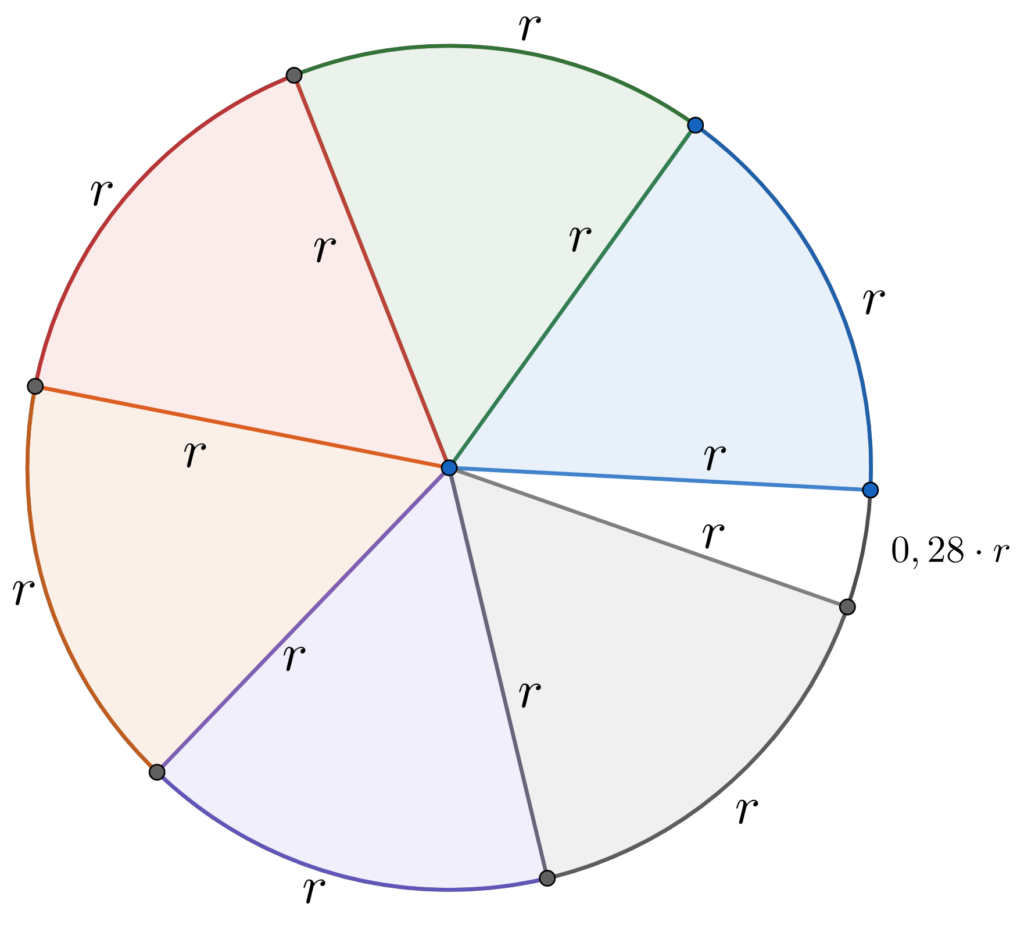
Dessa forma, dentro de uma circunferência cabem 6 raios completos mais \(0,28 \cdot r\). Cada setor desses limitado por dois raios e um arco de medida igual ao raio, vamos denotar por \(1 rad\), ou seja, em cada circunferência, cabem exatamente \(6,28 rad \). Vamos pensar agora nas medidas como diâmetro, ou seja, de dois em dois. Observe que cabem aproximadamente \(3,14\) diâmetros, numero que estamos muito familiarizados não é mesmo? Esse mesmo que você está pensando, o famoso \(\pi\). Dessa forma, uma circunferência completa equivale a \(2\pi rad \).

Trigonometria no círculo trigonométrico

A trigonometria que vimos até agora é baseada no triângulo retângulo e, a partir de agora, mostraremos como se comporta as razões trigonométricas dentro do círculo trigonométrico. Dessa maneira, note que o círculo trigonométrico é uma circunferência de raio igual a uma unidade de comprimento e que possui os eixos \(x\) e \(y\) de um plano cartesiano que passam pelo centro dessa circunferência. Por isso, acompanhe a imagem do círculo trigonométrico:

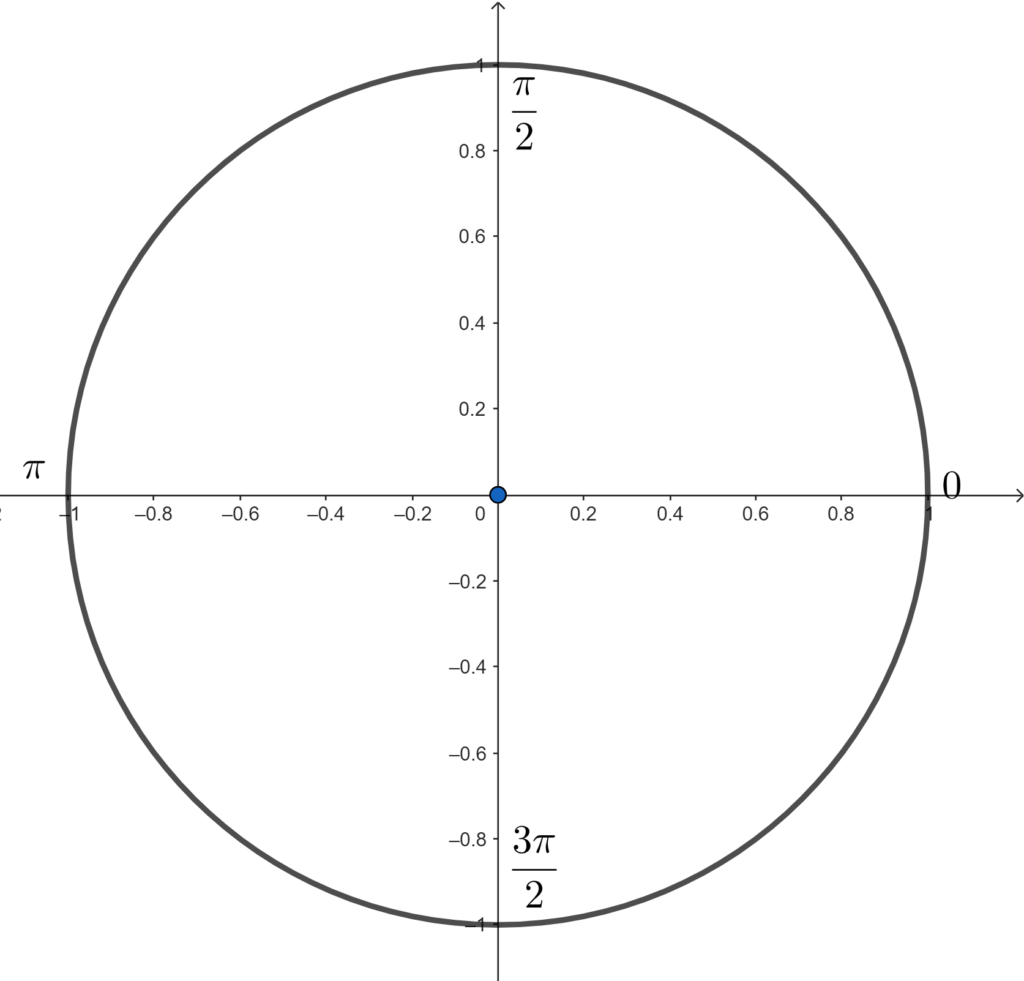
O ponto inicial desse círculo é o ponto de coordenadas \(\left(1,0\right)\), ou seja, na extrema direita da circunferência. Além disso, determinamos um segmento no ponto de partida até o centro da circunferência para realizar as análises dos ângulos que podem ser formados com outros segmentos da circunferência.

Razões da trigonometria no círculo trigonométrico

As razões seno, cosseno e tangente estão presentes no triângulo retângulo, mas também no círculo trigonométrico. Para calcular, observe a situação em cada uma delas:

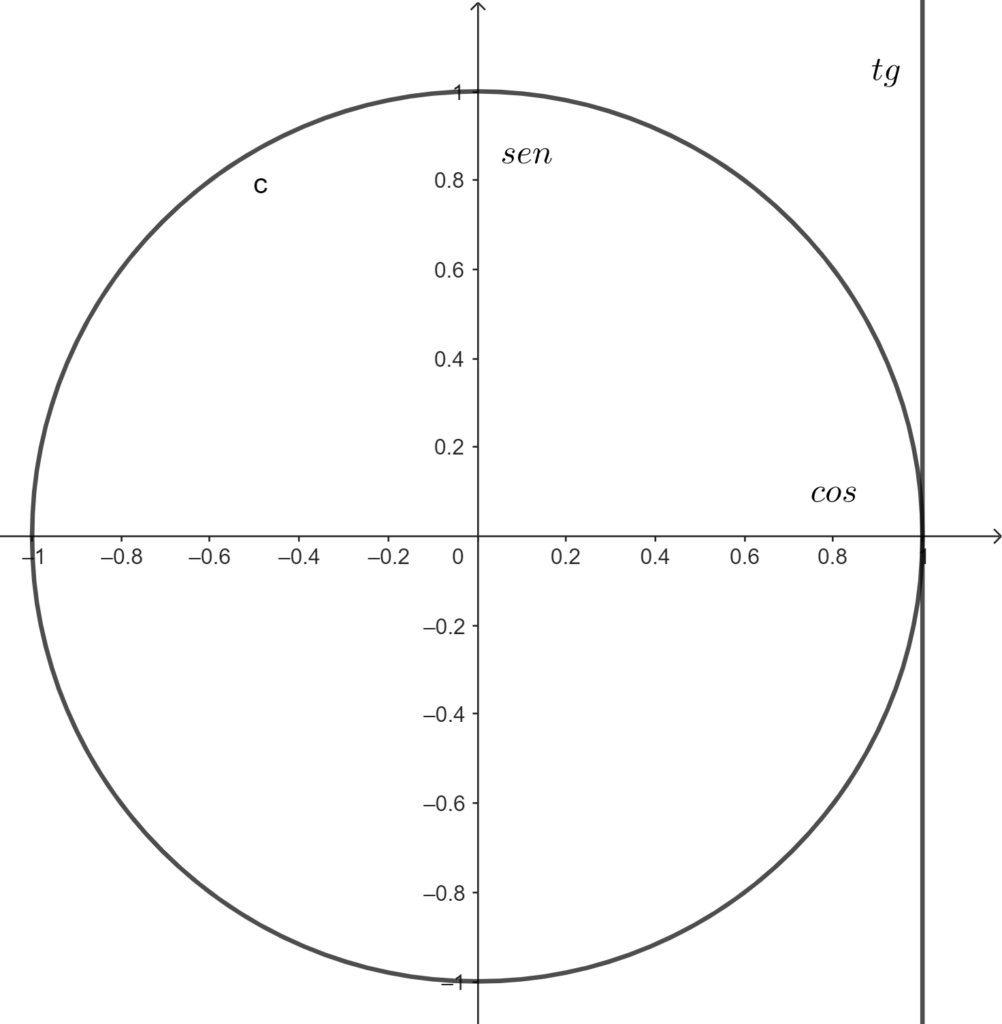
Conforme a imagem, podemos notar que definido um ângulo \(\alpha\), ao marcar um segmento partindo do centro do círculo com essa angulação é possível identificar algumas medidas. Ou seja, a coordenada \(y\) do ponto de intersecção do segmento com a circunferência é o seno do ângulo \(\alpha\). Por outro lado, a coordenada \(x\) desse mesmo ponto é equivalente ao cosseno do ângulo \(\alpha\). Além disso, ao prolongar o segmento até o eixo da tangente, descobrimos o ponto que distância uma medida de tangente de \(\alpha\) do eixo do cosseno.

Ângulos notáveis

Dentro da trigonometria, há os chamados ângulos notáveis, ou seja, os ângulos que podemos encontrar com facilidade e com ajuda da geometria, são eles: \(0º, 30º, 45º, 60º, 90º\) e seus correspondentes. Acompanhe abaixo a tabela com os ângulos notáveis:

	\(0º\) ou \(0 rad\)	\(30º\) ou \(\dfrac{\pi}{6} rad\)	\(45º\) ou \(\dfrac{\pi}{4} rad\)	\(60º\) ou \(\dfrac{\pi}{3} rad\)	\(90º\) ou \(\dfrac{\pi}{2} rad\)
\( sen \)	\(0\)	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{\sqrt{3}}{2}\)	\(1\)
\( cos \)	\(1\)	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{1}{2}\)	\(0\)
\( tg \)	\(0\)	\(\dfrac{\sqrt{3}}{3}\)	\(1\)	\(\sqrt{3}\)	-

Sinal dos quadrantes

Em função da representação cartesiana dos eixos \(sen \) e \(cos\), podemos definir o sinal dos quadrantes para razão: seno, cosseno e tangente. Veja a imagem:

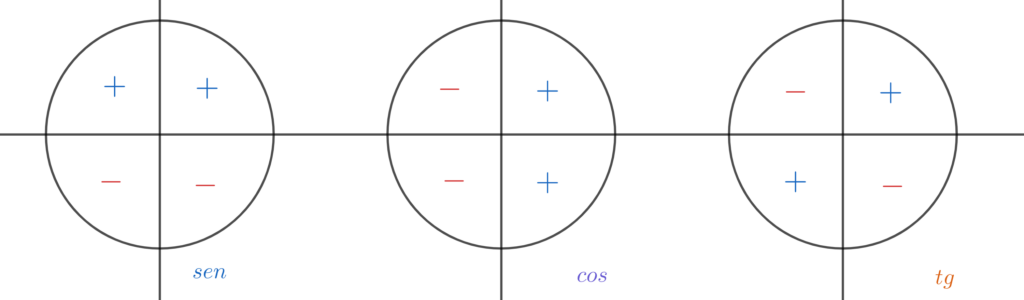
Note que os quadrantes são classificados de acordo com o plano cartesiano original, isto é, o primeiro quadrante é o superior direito, o segundo é o superior esquerdo, o terceiro é o inferior esquerdo e, por fim, o quarto é o inferior direito.

Ângulos correspondentes

Ângulos correspondentes são aqueles em que resultam um valor equivalente, em módulo, ao de outro ângulo quando aplicado nas razões trigonométricas. Por isso, acompanhe a imagem abaixo exibindo os ângulos correspondentes de 30, 45 e 60 graus:

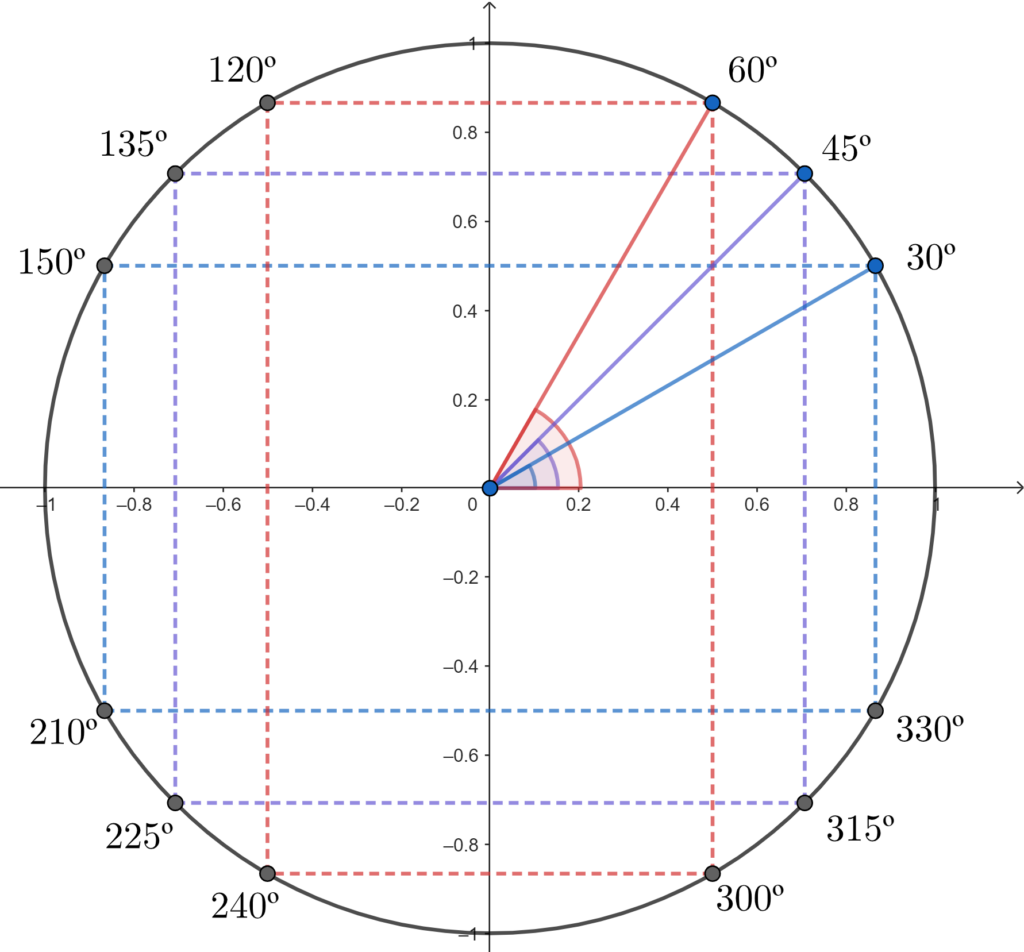
De acordo com a imagem acima, ela nos diz que as razões trigonométricas desses ângulos correspondentes são equivalentes, a menos de sinal. Dessa forma, para identificar o sinal de cada ângulo, devemos observar no sinal dos quadrantes em cada razão trigonométrica. Sendo assim, observe algumas relações abaixo:

• Segundo e primeiro quadrante: Senos com mesmo sinal e cossenos com sinal trocados

\[ sen \left( \alpha \right) = sen \left( \pi - \alpha \right) \text{ e } cos \left( \alpha \right) = -cos \left( \pi - \alpha \right) \]

• Terceiro e primeiro quadrante: ambos senos e cossenos com sinais trocados

\[ sen \left( \alpha \right) = -sen \left( \alpha - \pi \right) \text{ e } cos \left( \alpha \right) = -cos \left( \alpha - \pi \right) \]

• Quarto e primeiro quadrante: senos com sinais trocados e cossenos com mesmo sinal

\[ sen \left( \alpha \right) = -sen \left( 2 \pi - \alpha \right) \text{ e } cos \left( \alpha \right) = cos \left( 2 \pi - \alpha \right) \]

Reduções de arcos para a primeira volta

Para um skatista, é uma façanha realizar 900º com o seu skate. Perceba que 900º é 360º + 360º + 180º, ou seja, em tese o skatista que faz 900º realiza duas voltas e meia em torno de si e depois aterrissa no chão sem cair.

Na trigonometria, quando nos deparamos com um ângulo superior a 360º fazemos a mesma análise, ou seja, observamos quantas voltas cabem nesse ângulo, entretanto, o que realmente importa é qual a angulação após o número de voltas. Em outras palavras, para a trigonometria um ângulo de 900º resulta no mesmo valor para o seno, cosseno e tangente do que um ângulo de 180º, a diferença é apenas pelo número de rotações completas.

Para reduzir um ângulo \(alpha\), superior a \(360º\_ ou \(2\pi\), basta fazer a divisão de \(\alpha\) por 360º caso esteja em graus, ou dividir por \(2\pi\) caso esteja em radianos. Analisando o resultado do resto dessa divisão, teremos que a relação trigonométrica do ângulo original será igual a relação trigonométrica do resto obtido.

Relação fundamental e relações auxiliares da trigonometria

Neste instante, veremos que a relação fundamental da trigonometria é uma derivação do teorema de Pitágoras no triângulo retângulo formado através do círculo trigonométrico. Dessa maneira, acompanhe a imagem que demonstra esse triângulo e a relação fundamental da trigonometria:

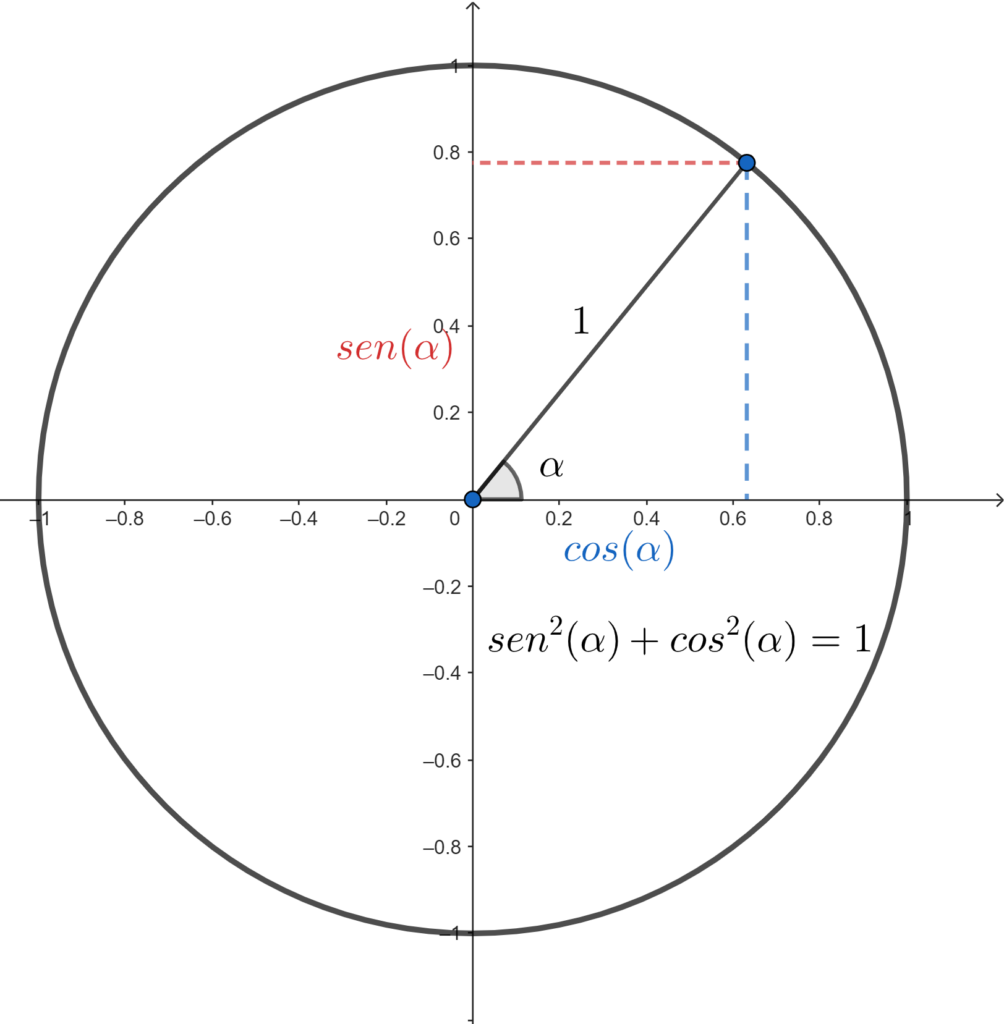
Conforme a figura, a relação fundamental da trigonometria é a aplicação do teorema de Pitágoras sobre o triângulo formado pelo ângulo \(\alpha\) na circunferência de raio \(1\), gerando a relação \( sen^2 \left( \alpha \right) + cos^2 \left( \alpha \right) = 1 \).

Por outro lado, as relações auxiliares são derivadas da relação fundamental da trigonometria, para demonstrá-las basta dividir a relação fundamental por \( sen^2 \left( \alpha \right) \) ou \( sen^2 \left( \alpha \right) \):

Operações com arcos

Na trigonometria, podemos realizar as operações com os arcos dentro das razões trigonométricas. Dessa forma, há as situações onde ocorre a soma, subtração, multiplicação e divisão de arcos. O que você mais precisa saber é sobre as duas primeiras operações e as operações com arcos duplos.

Soma e subtração de arcos

Para a soma e subtração de arcos, utilizamos algumas manipulações trigonométricas com a ajuda do teorema de Pitágoras que nos diz que o seno da soma e subtração de dois arcos é:

\[ \begin{eqnarray}
sen \left( \alpha + \beta \right) &=& sen \left( \alpha \right) \cdot cos \left( \beta \right) + sen \left( \beta \right) \cdot cos \left( \alpha \right) \\
sen \left( \alpha - \beta \right) &=& sen \left( \alpha \right) \cdot cos \left( \beta \right) - sen \left( \beta \right) \cdot cos \left( \alpha \right)
\end{eqnarray} \]

Além disso, para o cosseno, a relação é:

\[
\begin{eqnarray}
cos \left( \alpha + \beta \right) &=& cos\left( \alpha \right) \cdot cos \left( \beta \right) - sen \left( \alpha \right) \cdot sen \left( \beta \right) \\
cos \left( \alpha - \beta \right) &=& cos\left( \alpha \right) \cdot cos \left( \beta \right) + sen \left( \alpha \right) \cdot sen \left( \beta \right)
\end{eqnarray}
\]

Por outro lado, a tangente da soma e subtração de arcos é derivada dessas outras duas funções que resulta nas seguintes fórmula:

\[
\begin{eqnarray}
tg \left( \alpha + \beta \right) &=& \dfrac{tg \left( \alpha \right) + tg \left( \beta \right)}{1 - tg \left( \alpha \right) \cdot tg \left( \beta \right)} \\
tg \left( \alpha - \beta \right) &=& \dfrac{tg \left( \alpha \right) - tg \left( \beta \right)}{1 + tg \left( \alpha \right) \cdot tg \left( \beta \right)}
\end{eqnarray}
\]

E por último mas não menos importante, as operações de arcos duplos para as relações trigonométricas são:

\[
\begin{eqnarray}
sen \left( 2 \alpha \right) &=& 2 sen \left( \alpha \right) \cdot cos \left( \alpha \right) \\
cos \left( 2 \alpha \right) &=& cos^2 \left( \alpha \right) - sen^2 \left( \alpha \right) \\
tg \left( 2 \alpha \right) &=& \dfrac{2 tg \left( \alpha \right)}{1 - tg^2 \left( \alpha \right)}
\end{eqnarray}
\]

Funções Trigonométricas

Entendemos por função, uma relação \(f\) entre dois conjuntos \(A\) e \(B\) que satisfazem duas regras

• Para todo \( x \in A\), existe algum \( y \in B \) tal que \(f(x) = y\)
• Para todo \(x \in A\), existe apenas uma relação entre \(x\) e \(y\)

Sendo menos formal, no conjunto de saída \(A\) nenhum número irá ficar de fora da relação, e nenhum número de \(A\) se relaciona com mais de um elemento de \(B\).

Funções trigonométricas não seriam diferentes, elas satisfazem exatamente essas duas regras, porém trazem algumas peculiaridades. Veremos a seguir todas as propriedades sobre as principais características.

Função Seno

A função seno é definida por

\[
\begin{eqnarray}
f:\mathbb{R} &\longrightarrow & \mathbb{R} \\
x & \longmapsto & sen(x)
\end{eqnarray}
\]

A função \(sen\) é contínua para todos os números reais, ou seja, o seu domínio é \( D = \mathbb{R} \). Como você pode observar no gráfico acima, a imagem na função (\sen\) fica navegando entre \(-1\) e \(1\), dessa forma, o conjunto imagem é dado por \( Im = [-1, 1] \).

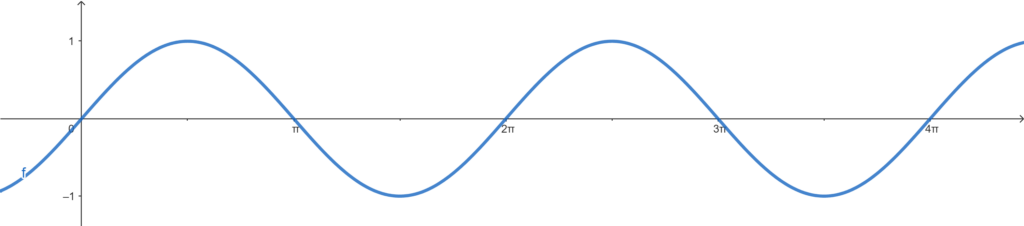
Repare também que a partir de um certo ponto, o gráfico se repete como se fosse uma cópia da parte anterior, o que não é surpresa para ninguém, em função do círculo trigonométrico, que independente de quantas voltas dermos com nosso ângulo, os valores estão sempre variando dentro do mesmo intervalo. Da origem até o ponto onde a função se repete, vamos chamar de período da função, e o período da função seno é de \( [0, 2\pi] \). Já a distância entre o maior e o menor ponto das função, iremos chamar de amplitude e a amplitude da função seno é dado pela imagem \( [-1, 1] \).

De forma mais geral, a função seno tem a seguinte lei:

\[ f(x) = A\cdot sen(B\cdot x + C) + D \]

Onde \( A, B \in \mathbb{R}^{*} \) e \( C, D \in \mathbb{R} \). O coeficiente \(A\) faz com que a amplitude de nossa função aumente ou diminua. Os coeficientes \(B\) e \(C\) vão alterar o período de nossa função, e por último, o coeficiente \(D\) faz com que o centro de nossa função fique deslocado.

Função Cosseno

Muito semelhante com o que fizemos para a função seno, a função cosseno é satisfeita pela seguinte lei:

\[
\begin{eqnarray}
f:\mathbb{R} &\longrightarrow & \mathbb{R} \\
x & \longmapsto & cos(x)
\end{eqnarray}
\]

A função cosseno também é contínua para todos os pontos da reta real, fazendo com que seu domínio seja \( D = \mathbb{R} \), e seus valores também variam entre \(-1\) e \(1\), fazendo com que sua imagem seja \( Im = [-1, 1] \) assim como a função seno.

IMAGEM AQUI

Como você pode observar no gráfico acima, ele é muito semelhante ao gráfico da função seno. Essa semelhança não é coincidência, pois a função cosseno também obedece o círculo trigonométrico, fazendo com que ela tenha periodicidade \( [0, 2\pi ] \).

De forma geral, a função cosseno é dada por

[ f(x) = A\cdot sen(B\cdot x + C) + D ]

Onde os valores de \(A, B, C\) e \(D\) satisfazem as mesmas condições da função seno, e executam as mesmas ações da função seno, alterando sua amplitude, periodicidade e altura do centro.

Como a Trigonometria cai no Enem e Vestibulares

Você meu caro aluno que está se preparando para o grande momento de sua vida e dando seu melhor pela tão sonhada aprovação, deve estar ansioso para saber como e quanto deve estudar de trigonometria para sua prova. Vamos aqui trazer um panorama de como o Enem costuma cobrar esse conteúdo e também a incidência dos principais vestibulares do Brasil.

Caso você esteja se preparando para o Enem, essa prova costuma cobrar trigonometria de uma forma bem básica e intuitiva, sempre contextualizada com problemas físicos envolvendo rotações, ondas, frequências. Com as noções básicas de funções e com as relações fundamentais, unidas a tabela de ângulos notáveis você estará bem munido de ferramentas para resolução dos problemas propostos. Trigonometria também não é a matéria queridinha do Enem, onde ao longo do tempo tivemos menos de 20 questões ao longo de todas as aplicações.

Já para os demais vestibulares (iremos pontuar sobre os vestibulares UEA, UERJ, Unicamp, Unesp e UFPR), já é cobrado de forma mais avançada os conhecimentos sobre funções e relações trigonométricas. Estar bem familiarizado com as noções de funções trigonométricas, período, amplitude, saber manipular ângulos para operar com somas e diferenças de arcos é imprescindível para se destacar em sua prova.

Exemplo 1

(Enem 2023)  O mastro de uma bandeira foi instalado perpendicularmente ao solo em uma região plana. Devido aos fortes ventos, três cabos de aço, de mesmo comprimento, serão instalados para dar sustentação ao mastro. Cada cabo de aço ficará perfeitamente esticado, com uma extremidade num ponto P do mastro, a uma altura h do solo, e a outra extremidade, num ponto no chão, como mostra a figura.

Os cabos de aço formam um ângulo \(\alpha \) com o plano do chão e instalação:

Por medida de segurança, há apenas três opções de instalação:

• opção I: \(h = 11\)m e \(\alpha = 30°\)
• opção II: \(h = 12\) m e \(\alpha = 45° \)
• opção III: \(h = 18\) m e \(\alpha = 60°\)

A opção a ser escolhida é aquela em que a medida dos cabos seja a menor possível.

Qual será a medida, em metro, de cada um dos cabos a serem instalados? 

1. \( \dfrac{22\sqrt{3}}{3} \)
2. \( 11\sqrt{2} \)
3. \( 12\sqrt{2} \)
4. \( 11\sqrt{3} \)
5. \( 22 \)

O comprimento \(x\) dos cabos é dado por:
\[ sen(\alpha ) = \dfrac{h}{x} \Rightarrow x = \dfrac{h}{sen(\alpha )} \] 

Para cada opção, temos:
\[ x_I = \dfrac{11}{sen⁡(30°)} = \dfrac{11}{\frac{1}{2}} Rightarrow x_I = 22 m \]
\[ x_{II} = \dfrac{12}{sen⁡(45°)} = \dfrac{12}{\dfrac{\sqrt{2}}{2}} \Rightarrow x_{II} = 12\sqrt{2} m \cong 16,9 m \]
\[ x_{III} = \dfrac{18}{sen⁡(60°)} = \dfrac{18}{\frac{\sqrt{3}}{2}} \Rightarrow x_{III} = 12\sqrt{3} m \cong 20,8 m \]

Logo, a medida dos cabos a serem instalados é de \(12\sqrt{2}\) m. 

Exemplo 2

(Uece 2018)  Se as medidas de dois dos lados de um triângulo são respectivamente \(7m\) e \(5\cdot \sqrt{2} m \) e se a medida do ângulo entre esses lados é 135 graus, então, a medida, em metros, do terceiro lado é:

1. 12
2. 15
3. 13
4. 14

Seja \(x\) a medida do terceiro lado. Logo, pela Lei dos Cossenos, encontramos:

\[
\begin{eqnarray}
x^2 &=& 7^2 + (5\cdot \qrt{2})^2 - 2\cdot 7 \cdot 5\sqrt{2} \cdot cos(135º) \\
x^2 &=& 49 + 50 - 70\sqrt{2} \left( -\dfrac{\sqrt{2}}{2} \\
x^2 &=& 99 + 35 \cdot 2 \\
x^2 &=& 169 \\
x &=& 13
\end{eqnarray}
\]

Portanto, resposta alternativa B).

🥇 Quer se preparar para o Enem e vestibulares com quem mais entende do assunto? A plataforma Aprova Total é a maior especialista no ensino digital e tem as melhores videoaulas e professores!