Fórmulas matemáticas para Enem e vestibulares

As fórmulas, sem sombra de dúvidas, facilitam qualquer resolução de exercícios. Aprenda como memorizá-las de modo mais prático!

07/11/2023

Professor olhando para lousa verde com fórmulas matemáticas escritas em giz branco

Acessibilidade

As fórmulas matemáticas são necessárias para resolver questões da prova do Enem e de todos os vestibulares do país. Neste texto, reunimos dicas de como memorizá-las de um jeito mais eficiente, além de mostrar quais são as principais fórmulas de cada grande área de estudo da Matemática para o Ensino Médio.

NAVEGUE PELOS CONTEÚDOS

Como memorizar fórmulas matemáticas

A priori, é importante destacar que a memorização das fórmulas ajuda você a passar por aquele perrengue no meio das provas. Porém, não devemos nos apegar em decorar as fórmulas em si, mas em entender o processo usado para formulá-las.

Por exemplo: em vez de usar a fórmula da área do setor circular de um círculo, deduzimos ela através de uma regra de três e da fórmula da área do círculo que é mais simples.

Por outro lado, em alguns casos, quando a dedução da fórmula é muito complexa, vale mais a pena decorar a fórmula por ser mais rápido. Um exemplo é a fórmula de Bhaskara, a fórmula resolutiva da equação do segundo grau. Sendo assim, veja a seguir algumas técnicas de memorização que ajudam a recordar fórmulas e informações necessárias.

Técnicas mnemônicas

Técnicas mnemônicas são processos que auxiliam na memorização de alguma coisa. Essas técnicas são funcionais por ativar um gatilho da memória sobre alguma coisa que remete a outra e assim por diante. Desse modo, veja a seguir algumas técnicas de memorização que podem ajudar a decorar fórmulas matemáticas:

Acrônimos: são palavras em que cada letra possui um significado. Exemplo: SUS (Sistema Único de Saúde);

Expressões: são frases que podemos relacionar com uma sentença de conceitos, geralmente sobre a letra inicial de cada palavra. Exemplo: bah, Bruninho, Karaca Moleque que Gata Top (bit, Byte, Kilobyte, Megabyte, Gigabyte e Terabyte);

Canções ou rimas: o ritmo da canção e a rima ajudam a recordar o conteúdo a ser memorizado. Exemplo: “Se vou ‘à’ e volto ‘da’, crase há. Se vou ‘a’ e volto ‘de’, crase para quê?”;

Palavras-chave: palavras que usamos para recordar determinado assunto. Exemplo: Na apresentação de um trabalho, selecionamos uma palavra para nos recordar do que temos que comentar. São os conhecidos tópicos dos slides, por exemplo.

Principais fórmulas matemáticas

Para facilitar a memorização, apresentamos as principais propriedades ou fórmulas matemáticas por grandes áreas. Sendo assim, você verá que a maioria das fórmulas é deduzida através de três conceitos principais: regra de três, produtos notáveis e fatoração e o teorema de Pitágoras. Desse modo, dê uma atenção especial a esses conceitos que podem ajudar muito na resolução de problemas, ok?! 😉

Razão, proporção e regra de três

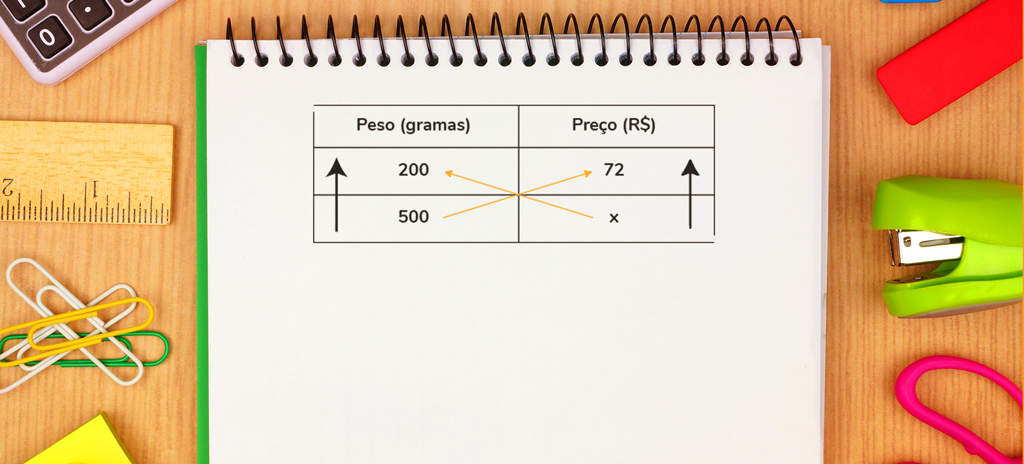
Se tratando de razão e proporção, o que devemos saber são as propriedades das grandezas diretamente e inversamente proporcionais e a formulação da regra de três. Veja a seguir como expressamos essas relações:

Caso a relação seja diretamente proporcional obtemos uma fórmula matemática em que uma grandeza é dividida por outra e essa razão é definida pela constante de proporcionalidade k.
Por outro lado, se a relação é inversamente proporcional, elas se dão por um produto em que a constante k é o resultado desse produto.

De acordo com a imagem acima, o que devemos recordar é que se uma grandeza aumenta e outra também aumenta, então elas são diretamente proporcionais. Por outro lado, se uma aumenta e outra diminui, então elas são inversamente proporcionais. Além disso, o k representa a constante que garante a proporcionalidade entre as grandezas.

Por fim, a regra de três consiste em relacionar as grandezas para encontrar um valor, podendo ser simples (duas grandezas com dois valores cada) ou composta (mais de duas grandezas com dois valores cada). Se as grandezas forem diretamente proporcionais fazemos a multiplicação cruzada. Se elas forem inversamente proporcionais, fazemos a multiplicação na horizontal.

Fique de olho, viu, estudante?! 👀 A matemática básica é um dos assuntos mais cobrados no Enem. Como treino, vale a pena se dedicar aos cálculos para não pisar na bola na hora da prova.

Produtos notáveis e fatoração

Após revisar razão, proporção e regra de três, veremos alguns manejos algébricos que usamos para simplificar equações e deduzir novas fórmulas. Tratam-se dos produtos notáveis e fatoração. Dessa forma, veja a tabela a seguir:

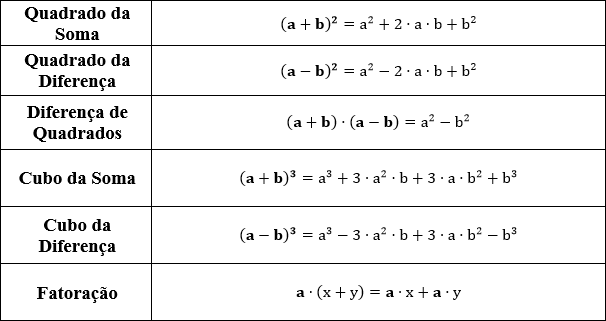
O quadrado da soma de dois números 'a' e 'b' é igual a 'a' ao quadrado mais duas vezes 'a' vezes 'b' mais 'b' ao quadrado.
De forma análoga, o quadrado da diferença de 'a' e 'b' é igual a 'a' ao quadrado menos duas vezes 'a' vezes 'b' mais 'b' ao quadrado.
Além disso, a diferença de quadrados é a soma de 'a' e 'b' vezes a diferença de 'a' e 'b' que é igual a 'a' ao quadrado menos 'b' ao quadrado.
Nesse momento, falamos do cubo da soma e diferença: o cubo da soma de dois valores 'a' e 'b' é 'a' ao cubo mais 3 vezes 'a' ao quadrado vezes 'b' mais 3 vezes 'a' vezes 'b' ao quadrado mais 'b' ao cubo. Do mesmo modo, o cubo da diferença de dois números 'a' e 'b' é 'a' ao cubo menos 3 vezes 'a' ao quadrado vezes 'b' mais 3 vezes 'a' vezes 'b' ao quadrado menos 'b' ao cubo.
Por fim, fatorar uma soma de dois fatores com um elemento em comum é obtermos um produto em que resulta nesse valor.

Você pode perceber na imagem acima que os produtos notáveis e as fatorações são equivalentes as suas outras representações, basta realizar a propriedade distributiva e chegar na igualdade definida.

Geometria plana

Na geometria plana, as fórmulas que mais importam são as áreas de figuras planas e as relações métricas de um triângulo retângulo. Dessa forma, acompanhe a tabela abaixo com as principais fórmulas da geometria plana:

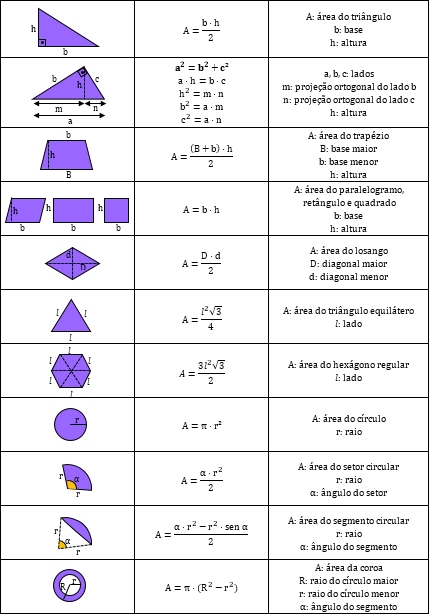
De acordo com a tabela acima, vemos diversas fórmulas da geometria plana. Nesse sentido, podemos observar algumas relações para que não seja necessário decorar todas as fórmulas.

Observe que o teorema de Pitágoras (a² = b² + c²) deduz a fórmula da área do triângulo equilátero e, além disso, somando seis triângulos equiláteros unidos pelo seus lados obtemos a área do hexágono regular.

Também podemos usar a regra de três para deduzir a área do setor e do segmento circular, supondo que sabemos a área de um círculo completo e do ângulo desejado.

Geometria espacial

Na geometria espacial, as principais fórmulas são as das áreas das superfícies dos sólidos e do volume que eles ocupam. Além disso, as áreas das bases e laterais são polígonos que vimos na geometria plana. Desse modo, veja abaixo as fórmulas necessárias para a geometria espacial:

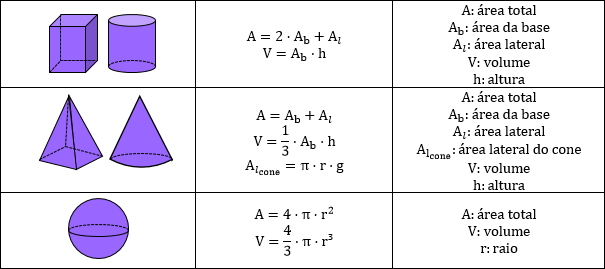
Na tabela vemos os prismas e cilindros no mesmo patamar por possuírem área e volume semelhantes. Nesse sentido, a área do prisma e do cilindro é igual a duas vezes a área da base vezes a área lateral. Por outro lado, o volume é o produto da área da base com a altura do sólido.
A pirâmide e o cone possuem a área igual soma das áreas da base e lateral. De outro modo, o volume é igual a um terço do produto da área da base com a altura. Além disso, temos o valor da área lateral do cone que é igual a 'pi' vezes o raio vezes a geratriz do cone.
Por fim, a área da esfera é igual ao quadruplo do produto de 'pi' com o raio ao quadrado. Ademais, o volume da esfera é igual a quatro terços vezes 'pi' vezes o raio ao cubo.

Como visto acima, as fórmulas de geometria espacial estão envolvidas com as de geometria plana. Isso ocorre porque tanto para calcular a área total quanto o volume dos prismas, pirâmides, cilindros e cones, é necessário conhecer a área da base.

Porém, a área da base são polígonos, ou seja, triângulos, retângulos, quadrados, hexágonos, isto é, figuras da geometria plana. Além disso, algumas relações das pirâmides e cones deduzimos pelo teorema de Pitágoras.

Funções

Nesse momento, chegamos no conteúdo de funções. Pensando nas funções do 1º e 2º grau, as fórmulas matemáticas mais usadas estão relacionadas à resolução de equações. Sendo assim, acompanhe abaixo as fórmulas e propriedades para esta classe de funções:

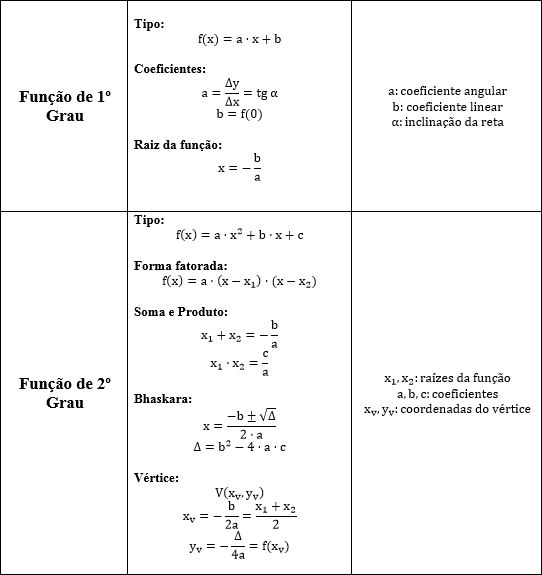
Segundo a tabela acima, vemos que a fórmula de Bhaskara é uma das mais complexas dentre as fórmulas matemáticas para ensino médio. Nesse caso, recomendamos memorizar a fórmula de Bhaskara.

Podemos encontrar as raízes da função do segundo grau pelo sistema de equações da soma e produto. Esse modo de resolver funções de 2º grau chama-se Relações de Girard, que garante uma relação entre as raízes e os coeficientes do polinômio para grau ( {2, 3, 4, …. , n } ).

Juros

Usamos os juros para a arrecadar dinheiro de taxas sobre valores em empréstimos, aplicações, etc. Sendo assim, veremos a seguir as fórmulas de juros simples e juros compostos.

Tanto nos juros simples quanto nos juros compostos, temos que:

J: valor dos juros.
C₀: capital inicial.
M: montante.
i: taxa de juros.
t: tempo aplicado.

Os melhores livros didáticos para estudar Ciências da Natureza e Matemática

Medidas de tendência central: o que são e como caem no Enem

Progressão aritmética e geométrica

Nas progressões aritméticas (P.A.) e geométricas (P.G.), o que mais importa é a fórmula do termo geral e a soma dos termos. Dessa maneira, veja abaixo as fórmulas desse assunto:

A progressão aritmética possui a fórmula do termo geral como 'a' índice 'n' igual a 'a' índice 'p' mais 'n' menos 'p' vezes 'r'. Além disso, a soma dos 'n' primeiros termos é igual a 'a' índice 1 mais 'a' índice 'n' vezes 'n' sobre 2.
Por outro lado, progressão geométrica tem como fórmula do termo geral 'a' índice 'n' é igual a 'a' índice 'p' vezes a razão elevada a 'n' menos 'p'. Ademais, a soma dos n primeiros termos da P.G. é 'a' índice 1 vezes a razão elevada a 'n' menos 1 sobre razão menos 1. De outro modo, há também a soma dos infinitos termos de uma P.G., quando a razão está entre 0 e 1, ela é igual a 'a' índice 1 sobre 1 menos a razão.

Em P.A. e P.G., a lógica é eficaz para a dedução das fórmulas. Observe, por exemplo, na P.A., que o segundo termo é o primeiro termo somado à razão; o terceiro é o primeiro termo somado ao dobro da razão, etc. De forma análoga, na P.G., o segundo termo é o primeiro termo multiplicado pela razão; o terceiro é o primeiro termo vezes o quadrado da razão.

Por fim, as somas dos termos são fórmulas que recomendamos ser memorizadas, pois sua dedução é um pouco mais complexa para realizar no dia da prova.

Análise combinatória

A partir de agora, veremos as principais fórmulas de análise combinatória: permutação, combinação e arranjo.

Há três tipos de permutação: simples, com repetição e circular.
A permutação simples de 'n' elementos é 'n' fatorial. A permutação com repetição de 'n' elementos com 'a', 'b', entre outros elementos repetidos é igual a 'n' fatorial dividido por 'a' fatorial, 'b' fatorial e demais elementos repetidos. Por fim, há permutação circular de 'n' elementos que nada mais é do que 'n' menos 1 fatorial.
Além disso, há a combinação de 'n' elementos tomados 'p' a 'p' que é igual a 'n' fatorial sobre 'p' fatorial vezes 'n' menos 'p' fatorial.
Por fim, o arranjo de 'n' elementos tomados 'p' a 'p' é 'n' fatorial sobre 'n' menos 'p' fatorial.

Além disso, lembramos que para diferenciá-las, determinamos o que a questão pede, se a ordem importa e se a natureza importa. Sendo assim, ordem refere-se aos diferentes modos de reordenação. Por outro lado, a natureza situa a distribuição de p elementos em n lugares possíveis.

Dessa forma, se somente a ordem importar, falamos de uma permutação. De outro modo, se somente a natureza for importante, estamos falando de uma combinação. Por fim, se ambas importarem, tanto a ordem quanto a natureza, deveremos utilizar o arranjo.

Trigonometria

Chegamos à trigonometria! Essa é a área da matemática que aborda as relações entre os ângulos e lados de triângulos. São as tão conhecidas razões seno, cosseno e tangente, e as principais fórmulas conhecidas dos arcos, além das relações trigonométricas.

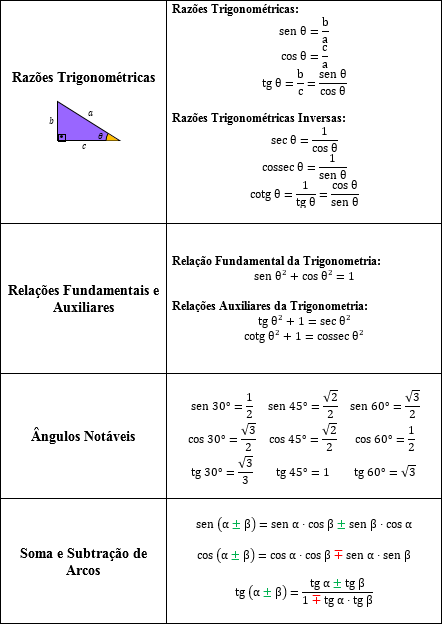
Como visto acima, a trigonometria possui algumas fórmulas complexas e várias informações suuuper importantes. Sendo assim, é prudente decorar algumas fórmulas desde que se saiba para o que elas servem. Dessa forma, podemos usar as técnicas mnemônicas e criar alguma sentença que ajude a memorizá-las. Uma dica é usar a palavra SOHCAHTOA para as razões trigonométricas:

SOH: Seno é o cateto Oposto sobre a Hipotenusa
CAH: Cosseno é o cateto Adjacente sobre a Hipotenusa
TOA: Tangente é o cateto Oposto sobre o cateto Adjacente

Além disso, para decorar o seno da soma ou diferença de arcos: “Minha terra tem palmeiras onde canta o sabiá: seno a, cosseno b; seno b, cosseno a” 🌴🐦.

Do mesmo modo, para decorar a fórmula do cosseno da soma ou diferença de arcos: “Coça-coça-senta-senta”. Desse modo, use sua imaginação para decorar mais fórmulas complexas.

Geometria analítica

Chegamos quase ao final deste post! E não poderíamos deixar de abordar as fórmulas usadas em geometria analítica: ponto médio, baricentro, distância entre dois pontos, distância de um ponto à reta e a área formada por pontos.

Primeiramente, o ponto médio tem coordenadas das médias aritméticas das coordenadas dos dois pontos analisados. De forma análoga, o baricentro possui coordenadas que representam a média aritmética das coordenadas de três pontos.
Nesse instante, enunciamos as distâncias: entre dois pontos e entre um ponto e uma reta.
No primeiro caso, a distância entre dois pontos é a raiz da soma dos quadrados das diferenças das coordenadas dos pontos. Por outro lado, no segundo caso a distância entre um ponto e uma reta depende de uma reta na equação geral. Além disso sua fórmula é igual ao módulo do coeficiente de 'x' vezes o 'x' do ponto mais o coeficiente de 'y' vezes o 'y' do ponto mais o coeficiente independente, tudo isso sobre a raiz da soma dos quadrados dos coeficientes de 'x' e 'y'.
Por fim, na geometria analítica, é importante falarmos da área de três pontos não colineares. Ela é dada pelo metade do módulo do determinante das coordenadas dos três pontos.

Em geometria analítica, algumas fórmulas podem soar diferentes das outras áreas porque trabalham no plano cartesiano. Porém, o teorema de Pitágoras pode ajudar a deduzir a fórmula de distância entre dois pontos.

Isso ocorre porque a distância é a hipotenusa de um triângulo retângulo de catetos iguais a diferença das coordenadas x e y dos dois pontos. Por isso, fique ligado nessa relação na hora de resolver a prova! 💡

* Colaborou nesta publicação: Bruno Pimpão