Regra de três simples: saiba tudo sobre o assunto

A regra de três é um dos assuntos mais conhecidos da Matemática. Além disso, ela é muito útil no contexto de grande parte das situações cotidianas, como abastecer o veículo, fazer uma receita, construir um prédio etc.

Ela, praticamente, está em tudo! Por isso, a tão aclamada regra de três é o tema deste texto. Entenda todos os processos e etapas para aplicar o conceito sempre que precisar. Bora?

Ah! Antes de começarmos com a regra de três simples, é essencial conhecer outro assunto importante da Matemática: razão e proporção. Para isso, recomendamos esta leitura, que explica os detalhes sobre o tema e suas propriedades. Assim, você pode compreender mais fácil o que vai ler a partir daqui!

Regra de três

A regra de três é um processo matemático com a função de auxiliar situações que encontramos proporções. Além disso, lembre-se que há dois tipos de proporções: diretas e inversas. Ambas expressam uma relação com duas ou mais grandezas, no sentido de que se uma grandeza é alterada implica que outra também será.

Em resumo, a regra de três é usada para encontrar uma dessas grandezas dentro de uma proporção. Para isso, lembre-se que uma proporção é nada mais do que uma igualdade entre duas razões. Além disso, uma razão é uma relação de uma grandeza/número com outro que pode ser expressa por meio de uma fração.

Dessa forma, podemos usar a regra de três para relacionar grandezas e encontrar o valor de uma incógnita em meio a uma proporção, ou seja, algo como:

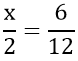
Porém, não somente isso, mas a regra de três tem como objetivo, também, encontrar as relações entre as grandezas. No caso acima, vemos que já existe uma relação: x está para 2 assim como 6 está para 12, trata-se de uma proporção entre duas razões. Portanto, nesse caso não precisamos utilizar do processo/estrutura de uma regra de três. Dessa forma, veremos agora como é montada a estrutura de uma regra de três simples.

Como montar uma regra de três simples?

Quando a relação entre as grandezas é diretamente proporcional, nesse caso, a técnica usada é multiplicar cruzado. Desse modo, obtemos relações diretas. Por outro lado, temos que é possível obter relações inversamente proporcionais e, assim sendo, a técnica será diferente.

Caso o exercício nos dê uma relação diretamente proporcional, então, significa que se uma grandeza aumentar ou diminuir, a outra irá aumentar ou diminuir também, nessa ordem. Dessa maneira, usamos as setas no mesmo sentido para identificar essa relação e, para formular a equação, multiplica cruzado os elementos, observe:

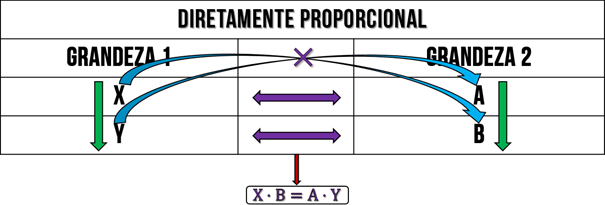
De outra forma, se o exercício nos der uma relação inversamente proporcional, ou seja, em que se uma grandeza aumentar a outra, por consequência, diminuir, usamos setas que apontam para sentidos opostos para identificar essa proporção. Além disso, a técnica a ser usada é a multiplicação em mesma linha, veja abaixo:

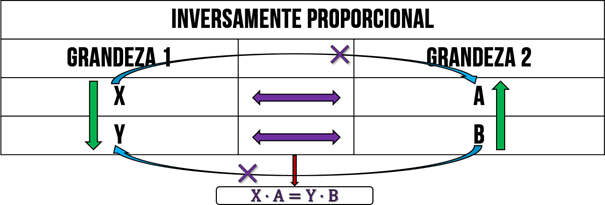
Isso ocorre pelo fato de que se a relação da grandeza 1 para a grandeza dois ser inversa, ou seja, quando X foi para Y aumentou e quando A foi para B diminuiu. Ou seja, em proporção podemos dizer que X ⋅ A = k, em que k é a constante da proporção. Do mesmo modo, podemos relacionar o Y com o B pela mesma constante: Y ⋅ B = k. Assim, é possível chegarmos a mesma equação feita na imagem acima.

Explicando o passo a passo da regra de três simples

Para ilustrar melhor esse método, usaremos o exemplo abaixo:

“Arnaldo está prestes a fazer aniversário e decide realizar uma festa com sua família. Para isso, ele realizará um churrasco para os seus convidados. Arnaldo sabe que para fazer um churrasco para sua família que reside em sua casa (ele, sua esposa e seus dois filhos), ele necessita de exatos 1,5 kg de carne. Portanto, quantos kg de carne serão necessários para que não falte e nem sobre comida no aniversário de Arnaldo, sabendo que 20 pessoas irão comer o churrasco e todas comem a mesma porção? ”.

Passo 1: interpretação

O primeiro passo ao lidar com um problema desse tipo é interpretar o que se pede. Portanto, perceba que o problema de Arnaldo é saber quantos kg de carne serão necessários para 20 pessoas comerem. Além disso, sabe-se que para 4 pessoas é preciso de 1,5 quilogramas de carne.

Nesse resumo do exemplo, podemos entender que há uma relação das 4 pessoas para o 1,5 kg de carne. Além disso, há uma relação entre as 20 pessoas para a quantidade de carne que essas 20 pessoas irão comer, no qual chamamos de x, em kg.

Passo 2: identificar as grandezas e montar a regra de três

Agora que você já identificou o problema e relacionou a quantia de pessoas com a quantidade de carne, resta encontrar as grandezas para poder montar a regra de três.

As grandezas nada mais são do que unidades contáveis, como por exemplo, peso, velocidade, tempo, temperatura, entre várias outras.

Você pôde notar duas grandezas no exemplo: a quantia de pessoas em unidades e a quantia de carne em kg. Sabendo disso, podemos organizar os dados em uma tabela, onde uma coluna será a quantia de pessoas e outra será a quantia de carne. Lembre-se que 1,5 kg de carne está relacionado com 4 pessoas e as 20 pessoas estão relacionadas com x kg de carne:

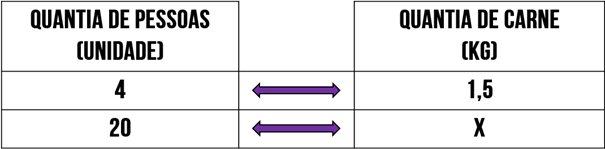
Note, neste instante, que as relações estão bem visíveis e, portanto, podemos identificar uma certa proporção.

Passo 3: identificar o tipo de proporcionalidade

Nesta etapa, você irá identificar qual é o tipo de proporção, se é direta ou indireta.

OBS: Lembrando que o nosso post de razão e proporção explica de forma detalhada por meio de exemplos a diferença entre relações diretamente ou inversamente proporcionais.

Sendo assim, perceba que a medida em que mais pessoas são convidadas é necessário mais comida para alimentar, e não menos. Dessa forma, temos uma grandeza diretamente proporcional e, sendo assim, podemos dizer, então, que se para 4 pessoas comem 1,5 kg de carne, 20 pessoas comerão mais ainda. Usamos setas apontando para o mesmo sentido quando a relação é direta:

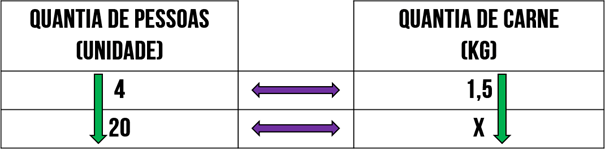
Ao descobrir o tipo de proporcionalidade, podemos então chegar a parte final da regra de três, a formulação da equação.

Passo 4: usar a regra de três para formular a equação

Para formular a equação e encontrar o valor x, ou seja, encontrar a quantia de carne para 20 pessoas, devemos usar a tabela criada e do tipo de proporção. Como a proporção desse exemplo é direta, então usamos a técnica de multiplicar cruzado, isto é, multiplicaremos uma diagonal e igualamos com a outra, veja abaixo:

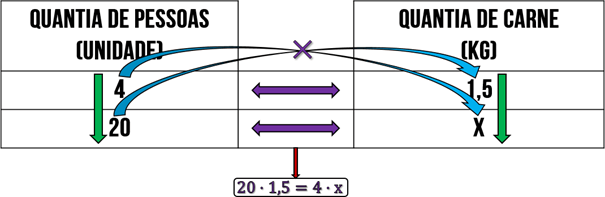
Com a equação pronta, podemos isolar a incógnita e obtermos a quantia de carne necessária:

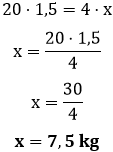
Dessa maneira, obtemos que para 20 pessoas comerem o churrasco de Arnaldo é necessário que ele asse 7,5 kg de carne. Perceba que, de fato, isso é verdade, pois podemos resolver esse exercício por meio de razão e proporção. Para isso, temos que lembrar as relações existentes entre a quantia de pessoas e a quantia de carne, 1,5 kg de carne para 4 pessoas é proporcional a x kg de carne para 20 pessoas, ou seja:

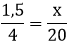
Ao realizarmos a “multiplicação cruzada”, obtemos a mesma equação que o método pela regra de três simples nos deu e, sendo assim, é por este motivo que esses dois conteúdos estão muito ligados.

Tipos de regra de três

Você deve ter notado que em momentos falamos regra de três e em outros falamos de regra de três simples. A regra de três simples é um dos tipos de regra de três, a mais comum e prática, usamos ela nos casos em que tratamos de duas grandezas. Além disso, há outro tipo, trata-se da regra de três composta e, nesse caso, teremos que olhar com mais cuidado as situações pois serão analisadas mais do que duas grandezas.

👉 Leia também:

Porcentagem: o que é, como calcular e exercícios resolvidos

Geometria espacial: tudo o que você precisa saber

Exemplos sobre regra de três simples

Agora que você já sabe o que é e como usar esse método de resolver questões, vamos exercitar com a ajuda de dois exemplos.

Exemplo 1

Para a produção de 250 biscoitos de polvilho são necessários 5 kg de polvilho azedo. Quantos kg de polvilho azedo será preciso para a produção de 1000 biscoitos?

Resolução:

Ao seguir os passos indicados, veremos que a interpretação do exemplo está clara: “5 kg de polvilho azedo para 250 biscoitos, por outro lado, quantos kg serão necessários para a produção de 1000 biscoitos? ”. Portanto, notamos que estamos lidando com uma relação diretamente proporcional, pois quanto mais biscoitos mais polvilho é necessário e, dessa forma, podemos montar a tabela com os dados obtidos:

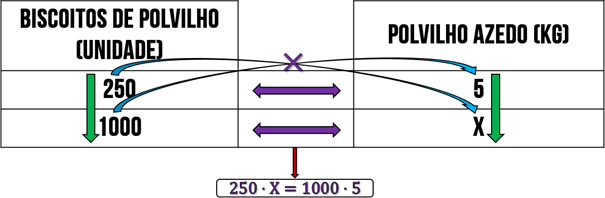
Com a equação formada, podemos isolar a variável e encontrar o valor de X:

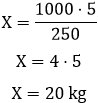
Por consequência, mostramos que a quantia necessária de polvilho azedo para a produção de 1000 biscoitos de polvilho são 20 kg.

Exemplo 2

Um motorista de ônibus levará os seus passageiros de uma cidade A até uma cidade B que distam 200 km uma da outra. A expectativa de viagem é de 2 horas e 51 minutos sem pausas. Entretanto, no final da viagem o cronômetro registrou um aumento de 21 minutos em relação a expectativa final da viagem. Dessa forma, calcule diferença entre a velocidade média esperada com a velocidade média real e assinale a opção aproximada:

OBS: Velocidade média é a razão entre a distância (km) e o tempo (horas).

a) 5,91 km/h

b) 6,21 km/h

c) 6,85 km/h

d) 7,65 km/h

e) 8,35 km/h

Resolução:

Veja que o enunciado pede a diferença entre a velocidade média esperada com a velocidade média real. O valor esperado da velocidade média é simples, pois, sabendo que a velocidade média é a razão entre a distância (200 km) e o tempo esperado (2 horas e 51 minutos, ou seja, 2 + 51/60 = 2,85 horas), obtemos:

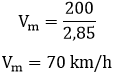
Perceba que, neste momento, temos o valor esperado da velocidade média. Dessa forma, podemos deduzir a velocidade média real por meio de uma regra de três simples. Para isso, observe que para o ônibus chegar no destino em 2 horas e 51 minutos (2,85 horas) ele deveria seguir uma velocidade média de 70 km/h. Todavia, o cronômetro registrou que o ônibus chegou 21 minutos a mais do que o esperado, ou seja, 3 horas e 12 minutos (3 + 12/60 = 3,2 horas) após a saída.

Sendo assim, obtemos uma relação entre a velocidade média e o tempo que é inversamente proporcional. Isso se deve ao fato que se a velocidade média aumentar o ônibus chegará mais rápido no seu destino, portanto, basta aplicar os dados na tabela:

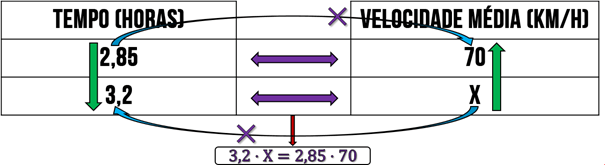
Isolando a incógnita:

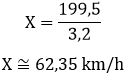
A diferença entre a velocidade média esperada e a velocidade média real é 70 – 62,35 = 7,65 km/h.