Medidas de tendência central: o que são e como caem no Enem

Olá, aprover! Neste artigo, vamos entender o que são as medidas de tendência central, mas, antes de nos aprofundar no assunto, é preciso conhecer o campo de estudo do qual elas fazem parte: a estatística.

Essa é uma ciência essencial para a interpretação e a análise de dados em diversas áreas do conhecimento. Por meio dela, é possível organizar, descrever e analisar informações quantitativas e qualitativas, permitindo-nos compreender padrões, tendências e relações entre variáveis.

O objeto de estudo da estatística são as variáveis e suas relações. As variáveis representam características que podemos medir e classificar em quantitativas ou qualitativas. Compreendê-las é importante para selecionar técnicas estatísticas adequadas e identificar padrões e relações nos dados.

Veja um exemplo de situação na qual a estatística pode ajudar:

Consideremos um diretor de escola que deseja identificar as idades dos alunos matriculados com o intuito de otimizar o planejamento de atividades e programas educativos. Ao coletar os dados de todos os estudantes, ele pretende avaliar se a distribuição etária na escola é representativa em relação à demografia da região em geral. Para isso, ele emprega as medidas de tendência central, como média, mediana e moda, a fim de capturar um valor central nas idades dos alunos e obter uma visão mais precisa do panorama etário da instituição.

O que são medidas de tendência central?

As medidas de tendência central desempenham papel valioso na estatística descritiva ao fornecerem uma representação concisa e significativa da distribuição dos dados. Por meio delas, conseguimos obter um valor que representa o centro dos dados, entendendo melhor a localização típica ou mais representativa das observações.

Essas medidas são essenciais para resumir grandes conjuntos de dados, facilitando a compreensão do comportamento geral da população ou da amostra em estudo. Quando as analisamos, podemos ganhar uma ideia melhor sobre as características centrais dos dados, tornando possível a identificação de padrões ou tendências e a comparação entre diferentes conjuntos de informações.

Conheça as principais medidas de tendência central

As três medidas de tendência central mais comuns são:

• média
• mediana
• moda

Vamos entender o que cada uma delas significa, como calculá-las e interpretar os seus valores?

Média aritmética simples

Uma das medidas estatísticas mais populares, a média aparece em vários contextos cotidianos e se destaca como uma ferramenta fundamental de análise. Ela está presente nas seguintes áreas:

• finanças
  a média é frequentemente mencionada em discussões sobre retornos de investimentos, taxas de juros e crescimento econômico;

• mídia
  notícias sobre economia, saúde, educação e outros assuntos costumar usar a média para apresentar estatísticas e tendências;

• esportes
  a média é utilizada para analisar estatísticas de desempenho de jogadores e equipes;

• estatísticas de vendas
  empresas calculam a média de vendas para avaliar como produtos e serviços;

• meteorologia
  previsões meteorológicas podem incluir a média histórica das temperaturas ou das precipitações para fornecer uma perspectiva sobre as condições climáticas;

• avaliações educacionais
  testes padronizados muitas vezes usam a média para relatar os resultados dos alunos.

A média aritmética representa o valor central de um conjunto de dados. Ela é obtida calculando a soma de todos os valores numéricos no conjunto e dividindo essa soma pelo número total de valores. Muitas vezes, a média é representada por um \(x\) com uma barra em cima \(\left( \overline{x}\right) \), sua fórmula pode ser expressa como na figura a baixo:

\(\overline{x}=\dfrac{x_1+x_2+x_3+\dots+x_n}{n}\)

Nesta fórmula, os valores \( x_1,\;x_2,\; ...,\;x_n\) representam os valores de cada elemento analisado e \(n\) representa quantidade de elementos.

Outra maneira de representar a fórmula da média é com o símbolo de somatório:

\(\overline{x}=\dfrac{\displaystyle\sum^{n}_{i=1}x_i}{n}\)

Ainda não compreendeu muito bem a ideia de média? Não se preocupe, vamos juntos ver um exemplo:

Exemplo de problema utilizando média aritmética

Carlos comprou três camisetas e pagou os seguintes preços: R$ 25, R$ 30 e R$ 20. Qual é a média aritmética dos preços das camisetas compradas por Carlos?

O primeiro passo é notar que Carlos comprou 3 camisetas, logo, o número de elementos que estamos calculando é 3. Além disso, sabemos o valor de cada camiseta, assim podemos realizar a sua soma:

Soma dos valores das camisetas = R$ 25 + R$ 30 + R$ 20 = R$ 75

Sabendo que a soma das camisetas resulta em R$ 75, basta dividir pela quantidade de camisetas, que é 3:

\(\dfrac{75}{3}\) = R$ 25

Assim, sabemos que Carlos gastou, em média, 25 reais em cada camiseta. Note que a fórmula apresentada anteriormente foi utilizada seguinte maneira:

\(\overline{x}=\dfrac{\text{R}\$\;25+\text{R}\$30+\text{R}\$20}{3}=\text{R}\$25\)

Média aritmética ponderada

A média ponderada é bem parecida com a média aritmética, a diferença é que cada valor das suas variáveis tem o que chamamos de peso. Assim, variáveis com pesos maiores possuem uma influencia maior sobre o resultado final da média ponderada.

Ela é especialmente útil quando diferentes elementos têm diferentes níveis de importância ou contribuição para a média final. Por exemplo, em um sistema de avaliação acadêmica, as notas podem ser ponderadas pelo número de créditos do curso. Dessa maneira, cursos com mais créditos têm um impacto maior na média final do estudante.

Para realizar o cálculo da média ponderada, devemos saber tanto o valor de cada variável como o valor de seus respectivos pesos. Denotando os valores das variáveis por \( x_1,\;x_2,\; ...,\;x_n\) e os seus respectivos pesos por \( p_1,\;p_2,\; ...,\;p_n\) temos a seguinte fórmula da média ponderada:

\(\overline{x}=\dfrac{x_1\cdot p_1+x_2\cdot p_2+x_3\cdot p_3+\dots+x_n\cdot p_n}{p_1+p_2+p_3+\dots p_n}\)

Não se esqueça de que n representa o número total de elementos no conjunto de dados.

Outra maneira de representar a fórmula da média ponderada é por meio de somatórios:

\(\overline{x}=\dfrac{\displaystyle \sum^{n}_{i=1}x_i\cdot p_i}{\displaystyle \sum ^{n}_{i=1}p_i}\)

Talvez, você tenha olhado para a fórmula e ficado com esta cara aqui 👇

Não entre em pânico! Se o seu foco são os vestibulares, no geral, eles não esperam que você saiba a fórmula desta maneira, mas é bom estar atento para não ser pego desprevenido! 😉

Exemplo de problema utilizando média ponderada

A tabela a seguir demonstra as notas de Ana no primeiro semestre na disciplina de matemática:

Categoria	Nota	Peso
Prova 1	8,5	3
Prova 2	7,5	3
Trabalho	5,0	2
Seminário	7,0	2

Sabendo que média é calculada de forma ponderada e Ana precisa ter pelo menos 6 na média para não ficar de recuperação responda, Ana ficou de recuperação?

Para calcular a média ponderada devemos primeiramente multiplicar cada nota pelo seu respectivo peso e somá-los:

\(8,5 \cdot 3 + 7,5 \cdot 3 + 5,0 \cdot 2 + 7,0 \cdot 2 = 72\)

Agora, devemos calcular a soma de todos os pesos:

\(3 + 3 + 2 + 2 =10\)

Com os valores obtidos, basta utilizar o resultado da soma das notas multiplicada pelo seu peso e dividir pela soma dos pesos:

\(\dfrac{72}{10}=7,2\)

Dessa maneira a média das notas de Ana é 7,2 e como 7,2 é maior que 6 Ana não ficou de recuperação. Note que a fórmula apresentada anteriormente foi utilizada seguinte maneira:

\(\overline{x}=\dfrac{8,5\cdot 3+7,5\cdot 3+5,0\cdot 2+7,0\cdot 2}{3+3+2+2}=\dfrac{72}{10}=7,2\)

Moda

A moda é uma medida de tendência central que representa o valor que ocorre com mais frequência em um conjunto de dados. Em outras palavras, a moda é o elemento que aparece mais vezes dentro do conjunto de observações. Algumas utilizações comuns da moda são:

• dados de votação
  em uma eleição, a moda pode representar a escolha mais popular entre os eleitores, ajudando a identificar o vencedor com base na preferência mais frequente;

• avaliações de produtos
  ao analisar avaliações de produtos, a moda pode mostrar qual é a classificação mais comum dada pelos consumidores, destacando a opinião predominante.

Você já ouviu a expressão "tal roupa está na moda"? A palavra remete à tendência do vestuário, ou seja, muitas pessoas estão utilizando a peça. E a ideia de moda é justamente esclarecer o elemento mais frequente de um conjunto.

A moda é especialmente útil quando se lida com dados de contagem, como categorias de produtos, cores ou números inteiros. Diferente da média, não se tem um fórmula específica para a moda, você precisa analisar o conjunto de dados e saber identificar qual o valor da moda.

Exemplo de problema utilizando moda

A tabela a seguir mostra a frequência de idades das pessoas que trabalham em uma fábrica

Idade	Frequência
20	15
25	12
30	8
35	10
40	5

Qual a idade predominante nesta fábrica?

Este exemplo é bem simples de resolver! Ao analisar a tabela, notamos imediatamente que a idade com a maior frequência é 20 anos, logo, sabemos que a moda da idade dos trabalhadores da fábrica é 20 anos.

É importante ressaltar que um conjunto de dados pode ter mais de uma moda, caso dois ou mais valores ocorram com a mesma frequência máxima. Nesse caso, o conjunto é chamado de bimodal (duas modas), trimodal (três modas) ou multimodal (mais de três modas). Observe um conjunto de dados fictícios:

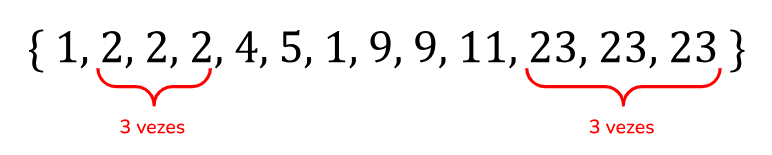
Perceba que o valor 2 e o valor 23 aparecem 3 vezes e são os elementos mais presentes no conjunto de dados, logo, eles se caracterizas como bimodal (duas modas).

O número 2 e o número 23 estão na moda! 😎

Outra ponto importante da moda é a sua interpretação gráfica, quando o gráfico possui um eixo de frequência, observe:

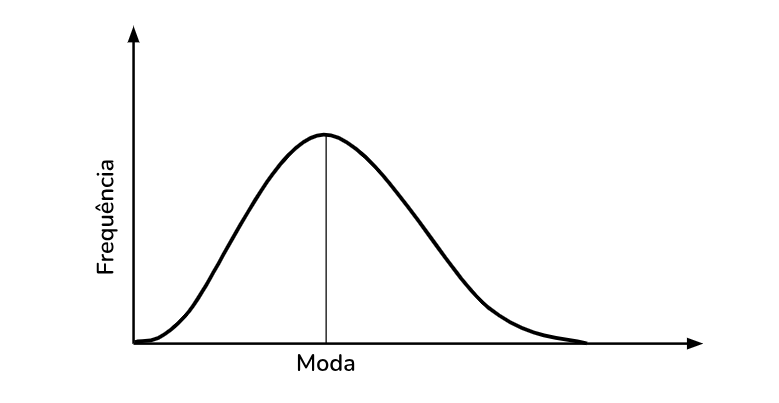
Note que o eixo da frequência relativa está na vertical, assim, a moda fica no ponto de maior altura do gráfico, representando o elemento que mais aparece ou possui maior frequência.

Mediana

A mediana é uma medida de tendência central que representa o valor central de um conjunto de dados que se organiza em ordem crescente ou decrescente. Isso quer dizer que a mediana é o valor que divide o conjunto de dados em duas partes iguais, com metade dos valores abaixo dela e metade acima dela.

Vale ressaltar que a ordenação em ordem crescente ou decrescente também é chamada de rol.

A mediana é particularmente útil quando se lida com conjuntos de dados que podem conter valores extremos (outliers), pois ela não é tão sensível a esses valores como a média aritmética.

Como calcular a mediana

Mediana é o valor que se encontra exatamente no meio de um conjunto de dados ordenado. Para calculá-la, siga estes passos:

• organize os dados em ordem crescente ou decrescente (rol);
• se o número de dados for ímpar, a mediana é o valor do meio;
• se o número de dados for par, a mediana é a média dos dois valores centrais

Problema utilizando mediana com número de elementos ímpar

Encontre a mediana do conjunto de dados a seguir, a qual representa a quantidade de ligações recebidas pelo telemarketing de uma empresa: 12, 17, 9, 22, 15

Note que o conjunto de dados possui uma quantidade de elementos ímpar (5 elementos), assim, a mediana será o elemento do meio.

Passo 1: organize os dados em ordem crescente: 9, 12, 15, 17, 22

\(9,\;12,\;\underbrace{15}_{\text{valor do meio}},\;17,\;22\)

A mediana é o valor do meio, que é 15.

Problema utilizando mediana com número de elementos par

Uma empresa possui os seguintes dados de idade (em anos) de seus 10 funcionários: 32, 28, 35, 41, 24, 29, 37, 48, 26, 31. Calcule a mediana das idades dos funcionários.

Note que o conjunto de dados possui uma quantidade de elementos par (10 elementos), assim, a mediana será a média dos dois valores do meio.

Passo 1: organize os dados em ordem crescente: 24, 26, 28, 29, 31, 32, 35, 37, 41, 48

\(24,\;26,\;28,\;29,\;\underbrace{31,\;2}_{\text{valores do meio}},\;35,\;37,\;41,\;48\)

Passo 2: como o número de dados é par (10 dados), a mediana é a média dos valores do meio, assim:

\(\dfrac{31+32}{2}=\dfrac{63}{2}=31,4\)

A mediana das idades do funcionários da empresa é 31,4.

Neste problema, entendemos que metade dos funcionários tem idade menor que 31,4 anos e a outra metade tem idade maior que 31,4 anos.

🚨Nunca se esqueça: o primeiro passo para calcular a mediana é organizar os elementos em rol! 🚨

👉 Leia também:

Regra de três: simples, composta, como calcular e exercícios

Geometria espacial: tudo o que você precisa saber

Como as medidas de tendência central caem no Enem e nos vestibulares?

As medidas de tendência central são frequentes nas questões de Matemática do Enem. Além de calcular a média, a mediana e a moda, as provas procuram avaliar a capacidade dos estudantes em compreender como essas medidas funcionam e como elas estão presentes em diferentes contextos.

Veja como as medidas de tendência costumam estar nas questões:

• comparação e contraste das medidas
  as provas podem pedir que os candidatos comparem e contrastem a média, a mediana e a moda, em situações nas quais as medidas são usadas para descrever diferentes aspectos de um conjunto de dados. É necessário interpretar quando uma medida pode ser mais apropriada do que outra.

• análise de contextos do mundo real
  o Enem busca vincular as medidas de tendência central a contextos do mundo real. Questões podem apresentar cenários envolvendo dados de pesquisas, estudos sociais, economia ou saúde e solicitar a interpretação das medidas nesses cenários.

• raciocínio crítico e tomada de decisão
  os candidatos podem ser desafiados a usar seu raciocínio crítico para tomar decisões com base nas medidas de tendência central, com questões em que é necessário escolher uma estratégia a partir das informações fornecidas pelas medidas. Isso destaca a importância de não apenas fazer cálculos, mas interpretar os resultados.

Para se sair bem nas questões que envolvem medidas de tendência central, é fundamental, além de memorizar as definições e as fórmulas, compreender como elas funcionam. 😀

Exercícios de medidas de tendência central

Confira alguns exercícios de medidas de tendência central:

Exemplo 1

(Enem)  O gráfico apresenta a taxa de desemprego (em %) para o período de março de 2008 a abril de 2009, obtida com base nos dados observados nas regiões metropolitanas de Recife, Salvador, Belo Horizonte, Rio de Janeiro, São Paulo e Porto Alegre.

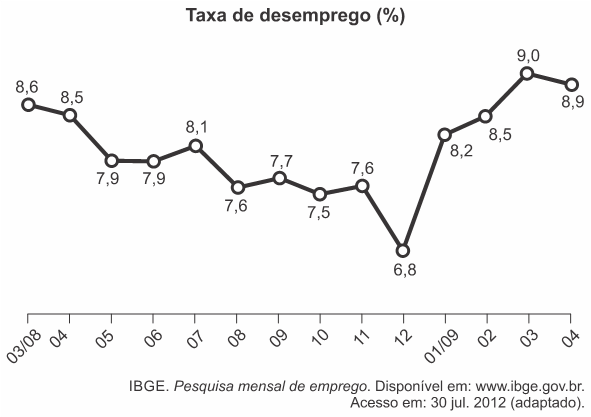
A mediana dessa taxa de desemprego, no período de março de 2008 a abril de 2009, foi de

a) 8,1%
b) 8,0%
c) 7,9%
d) 7,7%
e) 7,6%

Exemplo 2

(Fac. Albert Einstein - Medicina) Pedro e Luiza estão jogando cartas, sendo que, em cada carta está escrito algum número inteiro e positivo. Cada um inicia o jogo com 5 cartas e informa ao adversário a média dos números de suas cartas. No início do jogo, Pedro avisou que a média de suas cartas era 6 e Luiza avisou que a média de suas cartas era 4. Na primeira rodada Pedro passou uma carta para Luiza e Luiza passou uma carta para Pedro que estava escrito o número 1.

Se a média das cartas que Pedro passou a ter ficou igual a 4,8, o número da carta que Pedro passou para Luiza era

a) 4
b) 5
c) 6
d) 7 

Resposta [D]
Primeiramente, calculamos a média das cartas inicias de Luiza e Pedro:

Média Pedro - sendo x o valor da soma das 5 cartas inicias de Pedro temos que:
x/5 = 6 → x = 30

Média Luiza - sendo y a soma das 5 cartas inicias de Luiza e aplicando o mesmo raciocínio porem com os valores de Luiza, temos que:
y/5 = 4 → y = 20

Sabendo as médias das cartas inicias agora podemos calcular o valor após as trocas de cartas.
Sendo z o valor da carta que Pedro tirou e entregou para Luiza, temos que:
(x-z+1)/5 = (30 - z + 1)/5 = (21 - z)/5 = 4,8 Logo z = 7

Assim, o número da carta que Pedro passou para Luiza era 7.

Exemplo 3

(Upe-ssa)  Segundo matéria do Caderno Cidades do Jornal do Commercio, publicada em 8 de maio de 2016, um relatório oficial de assaltos a coletivos entre janeiro e abril de 2016 apontou os locais e as linhas de ônibus que mais sofreram esse tipo de violência no período citado.

Com base nessas informações, analise o gráfico publicado na referida matéria.

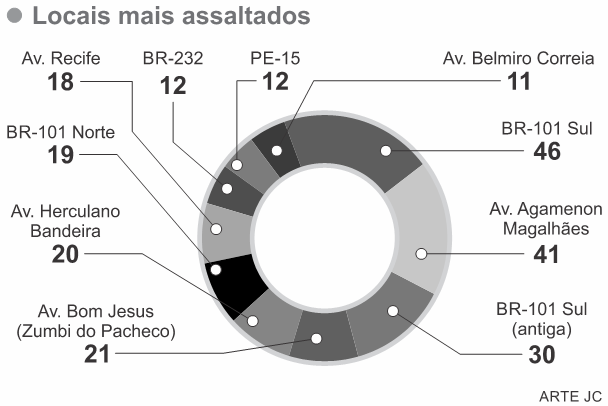
De acordo com o gráfico, a média, a mediana e a moda do número de assaltos por local são, respectivamente:

a) 19; 20 e 12.
b) 23; 19,5 e 12.
c) 19; 12 e 46.
d) 23; 12 e 19.
e) 19,5; 12 e 18.

Resposta [B]
A média, moda e mediana são três medidas estatísticas que ajudam a descrever e resumir um conjunto de dados. Elas representam diferentes aspectos da distribuição dos valores nesse conjunto. Assim, utilizando as respectivas fórmula e estratégias para encontrar as medidas de tendência central, temos:
Média - (11 + 12 + 12 + 18 + 19 + 20 + 21 + 30 + 41 + 46)/10 = 23

Mediana - ordenando os dados em rol temos: 11, 12, 12, 18, 19, 20, 21, 30, 41, 46.
Por se tratar de um conjunto com 10 elementos e 10 ser um número par, precisamos calcular a média aritmética dos elementos do meio, que são 19 e 20. Assim:
(19 + 20)/2 = 19,5 = Mediana

Moda - o único elemento que aparece mais de uma vez no conjunto de dados é o 12 aparecendo 2 vezes, logo 12 é a moda.

Dessa maneira, a média, a mediana e a moda do número de assaltos por local são, respectivamente: 23; 19,5 e 12.