O que é juros simples e como calcular

Os juros simples é um regime de capitalização muito importante para a matemática financeira, tanto é que ele faz parte da ementa escolar e dos conteúdos a serem cobrados tanto no ENEM quanto na maioria dos vestibulares. Além disso, o juro simples é semelhante aos juros compostos, outro regime amplamente utilizado para capitalização de forma exponencial. Ou seja, por ser exponencial, é mais vantajoso do que os juros simples.

Lembrando que ao final deste post você poderá baixar um eBook com questões sobre o assunto para exercitar tudo o que te ensinamos aqui!

Juros

Para entender como calcular os juros simples, devemos compreender que esse é um método de receber capital através do tempo estando sem o próprio dinheiro. Isso significa que em um empréstimo bancário, por exemplo, o banco cobrará uma taxa pelo tempo que você ficou usando o dinheiro dele. Ou seja, denominamos essa taxa por juros.

Em tese, o exemplo acima explica na prática os juros, dessa forma, podemos aprofundar esse conceito partindo para o cálculo de juros simples.

Cálculo dos juros simples

Para calcular os juros simples, devemos relembrar a ideia de que ele é calculado de acordo com o período do tempo com que o dinheiro foi emprestado, aplicado, etc. Além disso, para expressar a ideia do cálculo de diferentes exercícios que você verá pela frente, mostraremos três exemplos distintos de situações que podemos utilizar os juros simples. Primeiramente, você verá como calcular em uma dívida, após isso, como funciona em uma aplicação financeira e, por fim, em um empréstimo bancário.

Antes de demonstrarmos os exemplos, veremos que a fórmula dos juros simples é igual para todos os exemplos, ela é determinada como:

J = C₀ ⋅ i ⋅ t

Em que os juros são representados por J, o capital inicial por C₀, a taxa por i e o tempo por t. Além disso, sabe-se que o montante, representado por M, é a soma do capital inicial mais os juros, logo:

M = C₀ + J

M = C₀ + C₀ ⋅ i ⋅ t

Por fim, basta evidenciar o capital inicial para chegarmos em:

M = C₀ ⋅ (1 + i ⋅ t)

Juros simples em uma dívida

Para entender os juros simples nessa situação, suponha que uma pessoa tenha realizado uma compra de R$ 1.000,00 em uma loja e parcelou em dez prestações de R$ 100,00 cada. Essa loja admite uma taxa de 1% de juros simples a cada dia que passa após o vencimento de uma parcela.

Desse modo, suponha que essa pessoa pagará a primeira parcela após um dia do vencimento desta. Portanto, passado um dia do vencimento, ela pagará 1% de taxa a mais sobre o valor da parcela, ou seja, R$ 100,00 ⋅ 1% = R$ 1,00. Nesse sentido, se a pessoa pagasse dois dias após o vencimento, então, ela pagaria duas vezes a taxa sobre o valor da parcela, ou seja, R$ 100,00 ⋅ 2 ⋅ 1% = R$ 2,00. Consequentemente, se a pessoa fosse pagar após t dias, então ela iria pagar t vezes a taxa sobre o valor da parcela, isto é, R$ 100,00 ⋅ t ⋅ 1%.

Veja que podemos generalizar os juros para qualquer valor da parcela (C₀) e sobre qualquer taxa (i), ou seja:

J = C₀ ⋅ i ⋅ t

Observe que estamos calculando apenas o valor a mais nesse momento. Para calcular o valor total da parcela após t dias, deveremos incluir o valor original da parcela e somar com os juros, logo, R$ 100,00 + R$ 100,00 ⋅ t ⋅ 1%.

Generalizando o valor total (M) para qualquer valor da parcela (C₀) e para qualquer taxa (i), obtemos:

M = C₀ + C₀ ⋅ i ⋅ t

Aplicando o fator comum:

M = C₀ ⋅ (1 + i ⋅ t)

De modo geral, chamamos M de montante, C_0­ de capital inicial, i de taxa (no valor decimal), t do tempo passado após a operação e J do valor dos juros.

Juros simples em uma aplicação

Suponha que numa aplicação financeira, você aplique um valor de R$ 1.000,00 em seu banco. Por outro lado, o banco aplica um rendimento de 1% ao mês no regime de juros simples. Isso significa que a cada mês que passa o valor total aplicado receberá um acréscimo de 1% do valor aplicado. Ou seja, no primeiro mês o acréscimo será de 1% sobre R$ 1.000,00 que é R$ 10,00, logo, o valor total ficará R$ 1.010,00 no primeiro mês.

Do mesmo modo, passados dois meses da aplicação, o valor dos juros será duas vezes a taxa de 1% sobre o valor inicial da aplicação, isto é, 2 vezes R$ 10,00 de taxa. Portanto, o valor final no segundo mês da aplicação é R$ 1.020,00. Semelhante a isso, ao deixar aplicado o valor inicial por t meses, você obterá t vezes a taxa de 1% sobre o valor aplicado, isto é, t ⋅ R$ 10,00.

Perceba que, diferente dos juros compostos, em que a taxa é aplicada sobre o último valor, nos juros simples a taxa é sempre aplicada sobre o valor inicial. Além disso, o montante após t meses, em uma taxa i, em decimal, e um capital C₀, temos:

M = C₀ + C₀ ⋅ i ⋅ t

Colocando C₀ em evidência:

M = C₀ ⋅ (1 + i ⋅ t)

Da mesma maneira, o juro simples é calculado por:

J = C₀ ⋅ i ⋅ t

Juros simples em um empréstimo

Neste último caso, vejamos que é semelhante aos juros simples em uma dívida, pois se você pede um empréstimo, posteriormente você terá de pagar. Portanto, suponha que você necessite de um empréstimo bancário no valor de R$ 1.000,00 e pagará esse empréstimo em dez parcelas, ou seja, R$ 100,00 cada. Por outro lado, o banco aplicará uma taxa de 1% no regime de juros simples sobre as parcelas.

Nesse caso, veja que o banco aplica 1% sobre as parcelas, ou seja, haverá uma taxa de 1% sobre o valor de R$ 100,00, logo, R$ 1,00 a mais por mês. Desse modo, em vez de você quitar o empréstimo pagando R$ 100,00 por mês, você pagará R$ 101,00 por mês e, no total, R$ 1.010,00.

No primeiro mês, você pagará apenas uma parcela de R$ 101,00, como o valor da parcela inicialmente era de R$ 100,00 então os juros aplicados foram R$ 1,00. Por outro lado, no segundo mês você já pagou R$ 101,00 da primeira parcela e mais R$ 101,00 da segunda, isso significa que dos R$ 202,00 pagos, R$ 2,00 são acréscimos, ou seja, duas vezes o valor da primeira parcela. Esse processo se repete e chegamos nas mesmas fórmulas descritas nos outros exemplos, em que os juros simples são J = C₀ ⋅ i ⋅ t e o montante M = C₀ ⋅ (1 + i ⋅ t).

Distinção entre os exemplos

Nos três exemplos vocês puderam perceber que a fórmula não muda em nenhuma situação, mas exibimos três diferentes contextos que podem ocorrer em exercícios para que você possa interpretar de maneira correta. Note que nas situações de dívidas e empréstimos, a taxa incide sobre as parcelas. De outra forma, nas aplicações, a taxa incide sobre o valor colocado na aplicação. Portanto temos que tomar cuidado com qual capital inicial usar em cada exercício. É possível identificar as diferenças de acordo com a tabela abaixo:

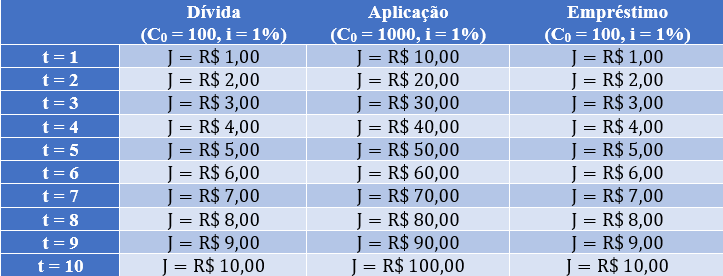
Veja que interpretar o problema é importantíssimo para entender com qual capital usarmos.

Exemplos de juros simples

Veremos exemplos de exercícios que lhe ajudaram a tirar de letra esse assunto.

Exemplo 1:

Maria empolgada com o lançamento de um celular que ela queria, realizou um empréstimo no valor de R$ 5.220,00 para pagar em parcelas mensalmente iguais durante um ano e meio. O banco por sua vez, aplicou uma taxa de 4% ao mês no regime de juros simples sobre cada parcela. O valor que o banco obteve de juros foi de

a) R$ 175,50

b) R$ 186,60

c) R$ 197,70

d) R$ 208,80

e) R$ 219,90

Resolução:

Primeiramente devemos analisar que o capital inicial são as parcelas. Como cada parcela é dividida mensalmente igual então devemos dividir o valor total do empréstimo pelo número dos meses. Como um ano e meio possui 18 meses, logo, = R$ 290,00 por parcela.

Dessa forma, como o R$ 290,00 representa nosso capital inicial, 18 meses é o tempo e a taxa é 4%, podemos descobrir o valor dos juros pela fórmula:

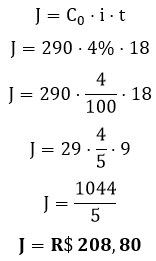
Portanto, a alternativa correta é a letra D.

Exemplo 2:

Pedro deseja investir uma quantia de R$ 4.500,00 em seu banco. Além disso, o banco oferece uma rentabilidade de 1,2% ao mês no regime de juros simples. Dessa forma, se Pedro deixar essa quantia aplicada durante 2 anos, o montante resgatado na retirada é

a) R$ 5.133,00

b) R$ 5.321,00

c) R$ 5.449,00

d) R$ 5.654,00

e) R$ 5.796,00

Resolução:

Como 2 anos representam 24 meses, podemos aplicar todos os dados do enunciado na fórmula do montante:

Logo, a opção correta está na letra E.