Juros compostos: veja como calcular, fórmulas e exemplos práticos

Os juros compostos, assim como os juros simples, são conteúdos introdutórios da matemática financeira e, dessa forma, são extremamente necessários para o entendimento de todos os conceitos posteriores desse ramo da Matemática.

Além disso, saber o que é e entender como calcular o juro composto é de extrema importância para a sua vida, pois esse assunto faz parte da sociedade como um todo. As principais aplicações dos juros compostos são em transações comerciais e bancárias, como por exemplo: pagamentos atrasados, financiamentos, entre outras formas de usá-lo.

Introduzindo os juros compostos

Anteriormente, explicamos as principais aplicações dos juros compostos no nosso cotidiano. A partir disso, podemos explicar por que usar esse regime de capitalização e como ele é capaz de gerar lucro.

Primeiramente, temos que entender que juros compostos é um método de obtenção de lucro, isto é, uma maneira de gerar riqueza e garantir ganho monetário. Sendo assim, isso explica o nosso primeiro questionamento feito no parágrafo anterior. Dessa maneira, resta demonstrar a vocês, como obtemos esse lucro.

Exemplo

Imagine um banco comum, cuja função principal é armazenar dinheiro de uma população. Partindo desse ponto, e supondo que o banco apenas guarda dinheiro das pessoas, então, ele não gera lucro. Dessa forma, o banco deve desenvolver métodos para ganhar dinheiro para realizar as suas manutenções e possivelmente ganhar lucro, entre elas, estão algumas taxas: de cadastro no banco; de saques; da manutenção da conta; de depósitos; de transações para outras contas, etc.

Perceba que apenas com isso, o banco já consegue receber uma boa quantia, entretanto, essas taxas não são a principal forma de obtenção de lucro em um banco, mas sim, os juros que o banco recebe com empréstimos ou financiamentos.

Note que a palavra empréstimo, remete a emprestar e, dessa maneira, é um tanto estranho a maneira de pensar como o banco pode ganhar dinheiro emprestando. Sendo assim, surge a ideia de juros, podendo ser simples ou compostos.

Juros

Como visto acima, os juros são a forma em que o banco mais consegue arrecadar dinheiro e, portanto, vamos entender como isso é possível. Para isso, suponha que uma pessoa realize um empréstimo bancário no valor de R$1000,00 e, além disso, essa pessoa desejará quitar essa dívida nos próximos 10 meses pagando uma parcela por mês. Perceba que, de forma lógica, a pessoa pagaria R$100,00 por mês e então sua dívida seria quitada, correto? Em partes sim, porém, o banco, para conseguir lucro, atribui uma taxa de um determinado valor sobre cada parcela. Essa taxa sobre o valor da parcela é o que chamamos de juros.

Dessa maneira, é possível fazer a primeira associação: como os juros representam o lucro que o banco obteve, então, o juro é o valor que a pessoa pagou no total com as taxas menos o valor do empréstimo.

Juros = Valor total com taxas - Valor do empréstimo

O valor total com as taxas chamamos de montante (M) e o valor do empréstimo chamamos de capital inicial (C₀), além disso, representaremos os juros pela letra J. Assim:

J = M - C

Tipos de juros: simples e compostos

Como explicitado no final da introdução de juros compostos, há dois tipos de juros: simples e compostos. A principal diferença entre eles é que os juros simples são taxas fixas sobre a parcela inicial. De forma distinta, os juros compostos são taxas fixas que se aplicam de acordo com a parcela anterior.

Para entender a diferença entre eles, suponha o exemplo anterior e que o banco aplique uma taxa de 10% ao mês para a quitação da dívida. Dessa forma, como R$100,00 é o valor da parcela, então, no primeiro mês, os juros representariam 10% desse valor. Isto é, portanto, R$10,00, resultando em um montante de R$110,00 no primeiro mês.

Como funciona nos juros simples?

Nos juros simples, a segunda parcela representa 10% do valor inicial, ou seja, 10% de R$ 100,00, portanto, o valor da segunda parcela é igual ao da primeira e, consequentemente, todas as parcelas terão o mesmo valor de R$ 110,00. Sabendo disso, como são 10 parcelas, então a pessoa pagará 10 vezes R$ 110,00 gerando um total de R$ 1100,00 de retorno ao banco e, de maneira lógica, o lucro obtido pelo banco é R$ 1100,00 – R$ 1000,00 = R$ 100,00.

Como funciona nos juros compostos?

Por outro lado, nos juros compostos, a segunda parcela representa 10% sobre o valor da parcela anterior. Isto é, 10% sobre o valor de R$110,00 (primeira parcela). Isso significa que o valor que a pessoa pagaria nesse mês seria de R$110,00 mais 10% desse valor. Ou seja, R$121,00, pois 10% de R$110,00 é R$11,00. Perceba que, nesse caso, os valores das parcelas serão diferentes a cada mês, mas os juros representaram sempre 10% da parcela paga no mês anterior.

Veja a tabela comparando os valores pagos a cada mês e o total arrecadado pelo banco no final dos 10 meses:

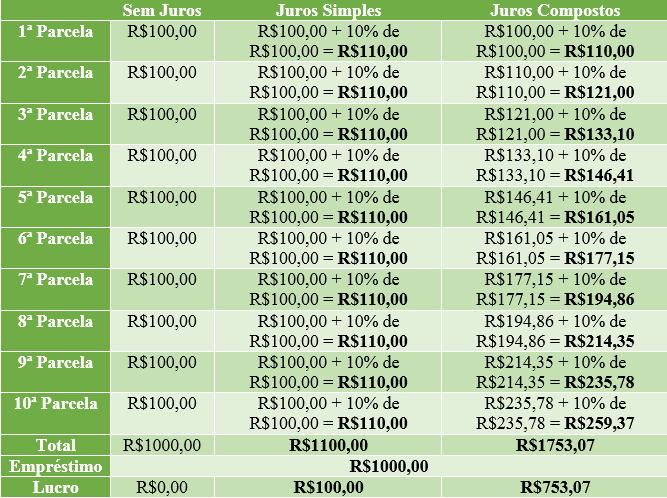
É possível analisar, também, de forma gráfica:

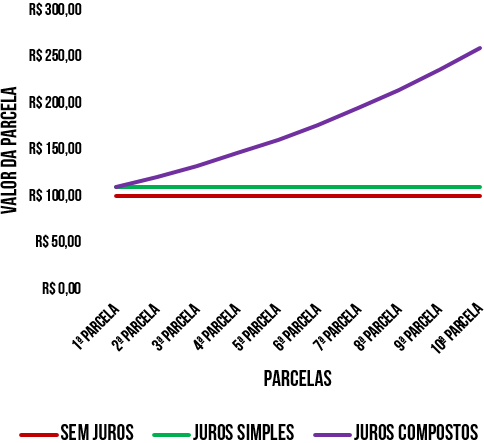
Note, na tabela, que a diferença do lucro que o banco arrecadou com juros simples e com juros compostos: um valor superior a R$ 650,00. Além disso, no gráfico, percebemos que o valor da parcela sem juros é constante, assim como, na de juros simples. Por outro lado, no regime a juros compostos, o gráfico cresce de forma exponencial. Dessa forma, é possível afirmar que os juros compostos são mais vantajosos do que os juros simples. Sendo assim, vamos entender como calculá-lo e realizar alguns exemplos.

Como calcular os juros compostos?

É de imediato pensar que há uma fórmula para calcular os juros compostos, pois percebemos um padrão na sua composição, portanto, exibimos abaixo a demonstração, em passos, de como calcular juros compostos.

Passo 1: primeiro montante

Dado uma aplicação financeira em uma conta bancária, com um determinado valor que chamaremos de capital inicial (C₀). Além disso, supondo que o banco rende esse capital mensalmente a uma taxa de x%, podemos afirmar, então, que o montante desse capital após o primeiro mês (C₁) é a soma do capital inicial com x% desse mesmo capital, isto é:

C₁ = C₀ + C₀ ⋅ x%

Note que essa fórmula nos remete a primeira associação feita de juros, em que o juro é a diferença entre o montante e o capital inicial, isto é, J = M – C₀.

Além disso, é perceptível que podemos isolar o montante da mesma forma que conclusão que obtemos acima, ou seja, M = C₀ + J. Por consequência, note que os juros equivalem a C₀ ⋅ x% e, portanto, podemos afirmar que os juros são:

J = C₀ ⋅ x%

OBS: Perceba que o montante nesse caso é equivalente a C­₁, pois ele é resultado do mesmo processo explicado na tabela.

Passo 2: segundo montante

Posteriormente, no segundo mês, em juros compostos, percebemos que a taxa x% será aplicada sobre o C₁, com isso o montante acumulado para o segundo mês, seria de:

C₂ = C₁ + C₁ ⋅ x%

Perceba, nesse momento, que podemos substituir C_1­ pelo valor que determinamos no início, isto é:

C₂ = (C₀ + C₀ ⋅ x%) + (C₀ + C₀ ⋅ x%) ⋅ x%

Note, ainda, que no interior dos parênteses, podemos colocar C₀ em evidência (se você não sabe como colocar números em evidência ou realizar o fator comum, recomendamos a leitura do nosso post sobre produtos notáveis), e obtermos o seguinte resultado:

C₂ = (C₀ ⋅ (1 + x%)) + (C₀ ⋅ (1 + x%)) ⋅ x%

Ademais, é possível colocarmos termos em evidência novamente, pois temos uma soma em que possuímos fatores comuns, observe abaixo:

C₂ = (C₀ ⋅ (1 + x%)) + (C₀ ⋅ (1 + x%)) ⋅ x%

C₂ = (C₀ ⋅ (1 + x%)) ⋅ (1 + x%)

Repare, neste instante, que como todos os fatores estão multiplicando, logo, é possível retirarmos os parênteses:

C₂ = C₀ ⋅ (1 + x%) ⋅ (1 + x%)

Finalmente, veja que podemos simplificar a igualdade acima por:

C₂ = C₀ ⋅ (1 + x%)²

Passo 3: comparando montantes e generalizando

Sabendo os valores do primeiro e segundo montantes, podemos relacioná-los tal como a sentença abaixo:

C₁ = C₀ + C₀ ⋅ x% e C₂ = C₀ ⋅ (1 + x%)²

Até agora não apareceu nada não é mesmo? Porém, ao colocarmos o C₀, da primeira equação, em evidência, resultamos em:

C₁ = C₀ ⋅ (1 + x%) e C₂ = C₀ ⋅ (1 + x%)²

É possível notar que a diferença entre C₁ e C₂ é que em C₂ a taxa se aplica duas vezes e, C₁, apenas uma vez. Além disso, ao expandir esses processos para os próximos meses, verificamos um padrão, em que o montante após n meses é a aplicação do capital inicial C₀ vezes a taxa elevado ao mesmo número n, portanto:

C_n = C₀ ⋅ (1 + x%)ⁿ

Simplificadamente, usamos a letra i para representar nossa taxa em valor decimal, pois é o valor que usamos para realizar contas com porcentagem, isto é, . Sendo assim, a fórmula do montante e dos juros compostos é a seguinte:

M = C₀ ⋅ (1 + i)^t e J = M – C₀

Perceba que M é o montante, C₀ é o capital inicial, i é a taxa de juros e t é o tempo aplicado. Além do mais, lembre-se que, sempre, a taxa de juros i e o tempo t devem estar na mesma unidade, ou seja, exemplo: “taxa de 2% ao ano”, significa que o tempo deve estar em ano(s) também.

Exemplos de juros compostos

Agora que você descobriu como se chega na fórmula de juros compostos, veremos alguns exemplos de como prosseguir em exercícios que pedem o montante, o capital inicial, a taxa de juros e o tempo de aplicação:

Exemplo com montante de juros compostos

No ano de 2005, João realizou um financiamento para a compra de sua casa no valor de 60 mil reais. O banco, então, atribuiu o pagamento em parcelas anuais durante 180 meses a uma taxa de juros compostos de 2,5% ao ano. Dessa forma, a quantia a mais que João irá pagar pela casa é aproximadamente:

OBS: Considere 1,025³⁰ ≈ 2,1 e que ≈ 1,45.

a) R$13.000,00

b) R$21.000,00

c) R$27.000,00

d) R$49.000,00

e) R$87.000,00

Resposta: [C]

João realizou um financiamento no valor de 60 mil reais, isso significa que esse valor é a quantia inicial. Além disso, o banco atribuiu o pagamento em parcelas anuais durante 180 meses, isto é, anos, portanto, João pagará o financiamento em 15 parcelas. Finalmente, o banco, para lucrar, inseriu um regime de capitalização a juros compostos de 2,5% ao ano, isto é, a cada ano o valor será 2,5% a mais que o da última parcela. Dessa forma, o valor que João pagou a mais pela sua casa é a quantia de juros e, para encontrá-la, devemos, primeiramente, encontrar o valor do montante após a quitação da dívida, isto é o valor após 15 parcelas, então:

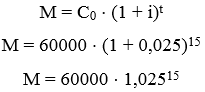
Observe que, geralmente, os enunciados disponibilizam dados nas questões. Nesse caso, foi dado que 1,025³⁰ ≈ 2,1 e que  ≈ 1,45. Note que 1,025³⁰ é o mesmo que (1,025¹⁵)² e, portanto podemos igualar ao 2,1:

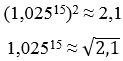
Perceba, então, que é dado no enunciado por 1,45, dessa forma, podemos substituir 1,025¹⁵ por 1,45:

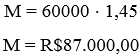
Como o enunciado pede o valor de juros que ele cobrou, então:

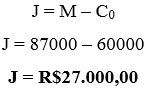
Exemplo com capital inicial de juros compostos

Vanessa decidiu aplicar uma quantia em um investimento bancário sobre o regime de juros compostos à uma taxa de 7% ao mês, durante 3 anos e meio. Ao final desse período, Vanessa obteve um lucro de R$14.553,00. Dessa maneira, determine a quantia aproximada que Vanessa aplicou no seu investimento.

OBS: Considere 1,07¹⁴ ≈ 2,58.

Resposta: R$ 900

Do enunciado, sabemos que Vanessa aplicou um capital no regime de juros compostos à uma taxa de 7% ao mês num período de 3,5 ⋅ 12 = 42 meses e gerou R$14.553,00. Sabendo disso, podemos determinar a quantia que Vanessa aplicou usando a fórmula de juros compostos, portanto:

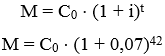
Observe que para calcular o montante, somamos o capital inicial mais os juros em cima dele, dessa forma, como os juros foram a quantia de lucro que Vanessa obteve, podemos substituir M por 14553 + C_0­:

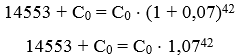
Note que, pelo enunciado, 1,07¹⁴ ≈ 2,58, portanto, perceba que 1,07⁴²= (1,07¹⁴)³, ou seja, 1,07⁴² ≈ 2,58³ ≈ 17,17. Dessa forma:

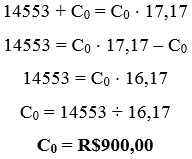
Exemplo com taxa de juros de juros compostos

Paulo comprou um carro financiado, a juros compostos, pelo seu banco. Sabendo que o valor do carro era de 33 mil reais e que no final do pagamento das 24 parcelas mensais o banco arrecadou 5 mil reais de juros. Determine a taxa de juros mensais, aproximada, que o banco de Paulo realizou para o financiamento e assinale a alternativa que melhor representa o resultado.

OBS: Utilize 1,00589 como aproximação de 1,1515^1÷24

a) 0,449%

b) 0,473%

c) 0,532%

d) 0,589%

e) 0,678%

Resposta: [D]

Pelo enunciado, o valor do carro é 33 mil reais, sendo assim, o capital inicial é 33 mil reais. Além disso, o banco arrecadou 5 mil reais de juros, portanto o montante deve ter sido 38 mil reais. Por fim, o número de parcelas é 24, que foram pagas mensalmente. Dessa forma, sabendo que a taxa também é mensal, resta saber o valor dela. Para isso, podemos substituir os valores na fórmula dos juros compostos, isto é:

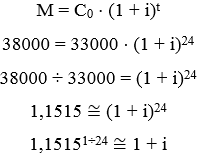
Note que o enunciado deu 1,00589 como aproximação desse valor, portanto:

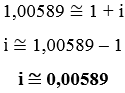
Exemplo com o tempo de capitalização de juros compostos

Para a compra de seu carro, Maria realiza um empréstimo bancário no valor de 25 mil reais a uma taxa de juros compostos de 2,5% ao mês. Sabendo que ao pagar a última parcela, o banco obteve, no total, 7 mil reais de juros, determine, aproximadamente, o número de meses que Maria levou para quitar sua dívida.

OBS: Considere log_1,025­1,28 ≈ 10

Resposta: 10 meses

Como o enunciado pede o número de meses que Maria levou para quitar a dívida de um empréstimo a juro composto, tendo o capital inicial (R$25.000,00), montante (M = C₀ + J = 25.000,00 + R$7.000,00 = R$32.000,00) e o valor da taxa mensal (2,5%), dessa forma, podemos montar a fórmula:

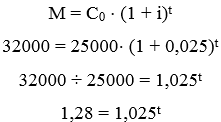
Observe que, nessa situação, encontramos uma equação exponencial de bases distintas e, quando isso ocorre, a solução para isso é aplicar logaritmo e suas propriedades nos dois lados da equação. Além disso, note que o enunciado nos deu uma afirmação importantíssima: “Considere log_1,025­1,28 ≈ 10”, dessa forma, o melhor dos casos é aplicar o logaritmo de base 1,025 nos dois lados da igualdade:

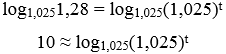
Utilizando as propriedades do logaritmo, podemos notar que:

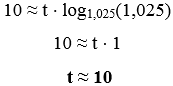
Perceba que, nos exemplos em que o enunciado pede o tempo de capitalização, é de extrema importância ter conhecimentos sobre logaritmos e propriedades dos logaritmos.