Progressão geométrica (PG): como calcular e fórmulas

Progressão geométrica é uma sequência numérica onde cada termo, a partir do segundo, é o termo anterior multiplicado por uma razão constante q. Mas essa é apenas uma definição resumida de um conceito importante para o Enem e grandes vestibulares.

E para ajudar você a aprender tudo sobre esse assunto, suas fórmulas e como calcular termos e razões, desenvolvemos esse conteúdo especial, com exemplos do cotidiano.

Por isso, vamos começar com uma pergunta simples: você aceitaria trabalhar em um emprego que o salário inicial é um centavo de real, porém, a cada mês, o seu salário dobra? Para entender se essa proposta salarial é boa, você precisa entender o que é uma progressão geométrica! Vamos descobrir como fazer esse cálculo?

O que é uma PG? Veja alguns exemplos

Semelhante ao que ocorre na progressão aritmética - onde cada termo é a soma constante de um valor ao anterior -, a progressão geométrica define cada termo por uma multiplicação de um valor constante ao termo anterior. Ou seja:

\[ a_{n+1} = a_ {n} \cdot q \]

onde \( a_{n} \) é o \(n\)-ésimo termo da sequência e \(q\) é o que chamamos de razão da progressão geométrica.

Exemplificando toda essa teoria, uma PG que tem como termo inicial \( a_1 = 1 \) e razão \(q = 3\) forma a seguinte sequência:

\[ \left\{ 1, 3, 9, 27, 81, 243, 729, \dots \right\} \]

A seguir, vamos ver as principais propriedades sobre progressões geométricas e aprender a identificar cada um de seus parâmetros com precisão.

Propriedades das progressões geométricas

Como a progressão geométrica é resultado de uma multiplicação sucessiva de termos iguais, muitas propriedades da multiplicação e da potência são herdadas por essas sequências. Algumas propriedades de PG são:

• Igualdade do produto entre termos equidistantes: admita o seguinte exemplo \( \left\{ 1, 2, 4, 8, 16, 32, 64, \right\} \). Ao multiplicarmos os termos \(1\) e \(32\), obtemos o mesmo resultado que na multiplicação entre \(2\) e \(16\), e ainda, entre \(4\) e \(8\) pois esses termos são equidistantes, como se eles tivessem um mesmo centro;

• Uma propriedade interessante é que se trabalharmos com um número ímpar de termos, a nossa sequência terá um valor central, e o quadrado desse valor satisfaz a propriedade acima, basta reparar que \(2\cdot 8 = 16 = 4^2 \);

• O termo central é também a média geométrica dos termos, pois \( \sqrt[7]{1\cdot 2 \cdot 4 \cdot 8 \cdot 16 \cdot 32 \cdot 64} = \sqrt[7]{2^{21}} = 8 \). O mesmo vale para quando o número de termos for par, a diferença é que a média geométrica dos termos da sequência será a média geométrica dos dois termos centrais;

• E caso você não saiba precisamente o valor da razão de uma progressão geométrica, basta dividir dois termos consecutivos \( \dfrac{a_{n+1}}{a_n} \).

Fórmula do termo geral de uma PG

Por definição, um próximo termo de uma PG é dado pelo produto do termo anterior com a razão, ou seja, \( a_{n+1} = a_n \cdot q \).

Repare como temos um problema ao dependeremos sempre do termo anterior, pois imagine que você precisa calcular o 50º termo de uma PG de razão 2. Para isso, você precisa encontrar o 49º termo, pois \( a_{50} = 2 \cdot a_{49} \).

Agora, você precisa encontrar o 48º termo porque você não conhece o valor de \( a_{49} \), e assim por diante.... Seria muito mais interessante conhecermos o primeiro termo e determinar qualquer outro a partir do primeiro, sem precisar passarmos pelos termos intermediários, não é mesmo?

Considere uma PG onde o primeiro termo é \( a_1 \) e a razão é \( q \). Iremos aqui construir a fórmula geral da PG, e temos o seguinte:

\[ \begin{eqnarray} a_1 &=& a_1 \\ a_2 &=& a_1 \cdot q \\ a_3 &=& a_2 \cdot q \\ a_4 &=& a_3 \\& \vdots & \\ a_n &=& a_{n-1} \cdot q \end{eqnarray} \]

Podemos ir substituindo cada termo anterior para reduzirmos o termo geral ao primeiro elemento de nossa sequência

\[ \begin{eqnarray} a_1 &=& a_1 \\ a_2 &=& a_1 \cdot q \\ a_3 &=& ( a_1 \cdot q ) \cdot q = a_1 \cdot q^2 \\ a_4 &=& (a_1 \cdot q^2) \cdot q = a_1 \cdot q^3 \\& \vdots & \\ a_n &=& (a_1 \cdot q^{n-2}) \cdot q = a_1 \cdot q^{n-1} \end{eqnarray} \]

Dessa forma, a equação geral da progressão geométrica é dada por:

\[ a_{n-1} = a_n \cdot q^n \]

👉 Leia também

Regra de três: simples, composta, como calcular e exercícios

Razão e proporção: propriedades e exercícios

Geometria espacial: tudo o que você precisa saber

Classificação das progressões geométricas

As progressões geométricas podem ser classificadas em função de sua taxa de crescimento e em função de sua finitude.

Dizemos que uma PG é finita, quando possui finitos termos, como \( \{ 2, 6, 18, 54 \} \). Por outro lado, dizemos que uma PG é infinita quando ela possui infinitos termos, por exemplo, \( \{1, 2, 4, 8, 16, 32, \dots \} \).

A seguir, vamos entender as principais classificações das progressões geométricas.

PG crescente

Dizemos que uma progressão geométrica é crescente, quando um termo qualquer é maior do que o seu termo antecessor, e assim sucessivamente para todos os termos da sequência.

A progressão \( \{1, 2, 4, 8, 16, 32, \dots \} \) é dita crescente pois \(2 >1; 4 > 2; 8 > 4 \) e assim, comparando eternamente.

Para fazer uma análise precisa sobre o crescimento de uma progressão geométrica, devemos trabalhar com 2 termos gerais consecutivos. Dessa forma, a PG será crescente se

\[ a_n < a_{n+1} \]

Outra forma de observarmos se uma PG é crescente é pelo valor de sua razão. Quando a razão \( q > 0 \), temos que a progressão geométrica será crescente. Em nosso exemplo, a razão é \( q = 2 > 0 \).

PG decrescente

De forma semelhante, dizemos que uma progressão geométrica é decrescente quando cada termo é menor do que o seu antecessor. A PG \( \{ 81, 27, 9, 3, 1 \} \) é decrescente, pois \( 27 < 81; 9 < 27; 3 < 9\) e \( 1 < 3 \).

Para casos onde a sequência é finita, você até pode comparar os termos um por um, porém esse processo se torna muito trabalhoso e demorado quanto mais termos uma PG tiver. E se houver infinitos termos, teríamos que ficar comparando infinitamente.

Desse modo, devemos sempre analisar a relação entre termos gerais consecutivos. Dizemos que uma PG é decrescente quando

\[ a_n > a_{n+1} \]

Fazendo uma análise do comportamento da PG em função de sua razão, temos que a progressão geométrica será decrescente quando \( 0 < q < 1 \). Realizando a divisão de dois termos consecutivos, temos que a razão de nosso exemplo é \( q = \dfrac{1}{3} \), que por sua vez está entre \( 0 \) e \(1\).

PG oscilante

Assim como nós, as progressões geométricas também possuem "alterações de humor". Ora elas estão positivas e animadas, ora estão negativas e para baixo. Isso se dá em relação ao sinal de sua razão.

Brincadeiras à parte, quando uma progressão geométrica possui razão \( q < 0 \), os sinais dos seus termos ficarão em alternância. Observe o comportamento da PG onde o termo inicial é \( a_1 = 2 \) e sua razão é \( q = -3 \). Os seus termos serão:

\[ \{ a_1 = 2, a_2 = -6, a_3 = 18, a_4 = -54, \dots \} \]

Conforme a regra de potências, quando uma base negativa é elevada a um expoente par, o resultado é positivo. Já quando a base negativa é elevada a um expoente ímpar, o resultado é negativo.

PG constante

Relembrando um pouquinho as propriedades da multiplicação, temos que \( 1 \) é o elemento neutro da multiplicação, ou seja, qualquer número multiplicado por \(1\) resulta no próprio número.

Dito isso, uma progressão geométrica será constante quando a sua razão for igual ao elemento neutro da multiplicação, em outras palavras, temos que \( q = 1 \).

Considere a PG onde \(a_1 = 5\) e \(q = 1\), os seus termos serão

\[ \{ 5, 5, 5, 5, \dots \} \]

Uma PG que é quase constante é quando a razão \(q = -1\). Dessa forma, ela será constante se olharmos apenas para os índices pares, ou apenas para os índices ímpares.

De nosso exemplo anterior, a PG completa é \( \{ 5, -5, 5, -5, \dots \} \). Se separarmos em índices pares e índices ímpares, teremos duas sequências onde, de forma disjunta, serão constantes \(5\) e \(-5\).

Soma dos termos de uma PG

Pelo fato de todos os termos de uma PG serem escritos em função do primeiro termo, conseguimos estabelecer uma relação entre a soma dessas sequências.

Tal soma pode ser finita ou infinita, e aqui iremos apresentar um conceito que pode até assustar você, mas não há o que temer!

Somas finitas de progressões geométricas

Primeiro, vamos trabalhar com as somas finitas de progressões geométricas. Como o próprio nome diz, queremos somar apenas alguns termos de cada progressão, quantidade essa que pode ser \(2, 3, 10, 1001928318273981 \), depende muito do que você deseja realizar ou do que o problema está pedindo.

Mas não se preocupe, você não vai precisar realizar essa soma de forma arcaica!

Sabemos que os termos de uma progressão geométrica são \( \{ a_1, a_1\cdot q, a_1 \cdot q^2, a_1 \cdot q^3 \dots \} \). Ao realizarmos a soma desses valores, temos que

\[ \begin{eqnarray} a_1 + a_2 + a_3 + \cdots + a_n &=& a_1 + a_1 \cdot q + a_1 \cdot q^2 + \cdots a_1 \cdot q^{n-1} \\ a_1 + a_2 + a_3 + \cdots + a_n &=& a_1 \cdot \left( 1 + q + q^2 + q^3 + \cdots + q^{n-1} \right) \end{eqnarray} \]

Essa expressão algébrica que surgiu dentro do parênteses tem um detalhe muito interessante: se você multiplicar essa expressão por \(q - 1\), é possível simplificar os termos e reescrevê-la como:

\[ \left( 1 + q + q^2 + q^3 + \cdots + q^{n-1} \right) \cdot (q - 1) = q^n - 1 \]

Mas atenção! ⚠️ Não podemos sair por aí multiplicando coisas sem termos certeza de que se trata do elemento neutro da multiplicação! Para isso, vamos multiplicar o lado direito de nossa igualdade da soma da PG por \( \dfrac{q-1}{q-1} = 1 \). Dessa forma,

\[ \begin{eqnarray} a_1 + a_2 + a_3 + \cdots + a_n &=& a_1 \cdot \left( 1 + q + q^2 + q^3 + \cdots + q^{n-1} \right) \cdot \dfrac{q-1}{q-1} \\ a_1 + a_2 + a_3 + \cdots + a_n &=& \dfrac{a_1 \cdot (q^n - 1)}{q-1} \end{eqnarray} \]

Temos então que a soma de \(n\) termos de uma PG é dada pela expressão:

\[ S_n = \dfrac{a_1 \cdot \left( q^n - 1\right) }{q-1} \]

Portanto, cada vez que você precisar somar uma PG finita, basta que você conheça o primeiro termo dessa PG, qual a sua razão, e quantos termos você irá somar.

Exemplo de soma finita de uma PG

Vamos resolver um exemplo para fixar as ideias! Considere a PG \( \{ 1, 2, 4, 8, 16, 32, 64, 128, 256 \} \), temos que o primeiro termo é \(1\), e para encontrar a razão, basta dividirmos dois termos consecutivos: \(q = \dfrac{2}{1} = 2 \). Temos à disposição, nove termos a serem somados. Dessa forma, a expressão resulta em:

\[ S_9 = \dfrac{1 \cdot ( 2^9 - 1) }{2 - 1} = \dfrac{512 - 1}{1} = 511 \]

💡 Repare que sempre que somarmos de modo finito, o resultado será um valor finito e mensurável, um número assim como estamos acostumados.

Somas infinitas de progressões geométricas

Quando as somas são infinitas, temos duas possibilidades:

• a soma resulta em um valor numérico;
• a soma "explode".

Calma! Progressões geométricas são inofensivas. O sentido de "explodir" a soma é que o resultado fica tão grande (tanto positivo como negativo) que não temos mais como mensurar o seu valor. Nesse caso, costumamos dizer que a soma tende ao infinito, ou que se aproxima do infinito ( \( \infty \) ).

Esse processo irá ocorrer sempre que a razão da PG for maior do que (1) ou menor do que \(-1\). De forma resumida, quando \( | q | > 1 \).

Agora, no caso de somas que resultam em um valor numérico, vamos fazer um exercício de abstração. Imagine que você adiciona coisas infinitamente a um todo e esse todo não se altera, quase como se essas coisas - por mais que diferentes - fossem vários zeros.

Quando uma soma infinita atinge um certo valor numérico mensurável, ou seja, que conseguimos dizer com exatidão o seu valor, dizemos que essa soma converge para tal valor.

Para que a soma infinita de uma PG atinja esse valor de convergência, precisamos que a razão \(q\) esteja entre \(-1\) e \(1\) (lembrando que deve ser diferente de zero). Essa condição é necessária, pois quanto mais aumentarmos a potência, mais próximo de \(0\) a potência se tornará, fazendo com que cada soma afete menos o resultado final.

A formulação de infinitude é algo complexo para abordarmos aqui, mas imagine que duas coisas são tão próximas e parecidas que, ao olharmos de forma geral, não há diferenças.

Semelhante a um floco de neve, ao vê-los caindo do céu, não se percebe diferença entre eles. Porém, ao olharmos de forma microscópica, nenhum é exatamente igual ao outro, porém é uma diferença tão insignificante que assumimos que eles são iguais.

Exemplo de cálculo de soma infinita de PG

Pela fórmula da soma finita \( S_n = \dfrac{a_1 \cdot \left( q^n - 1 \right) }{q-1} \), considere que o seu valor \(n\) irá crescer e crescer sem parar. Como o \(q\) é um valor diferente de zero que está entre \(-1\) e \(1\), por exemplo \(q = 0,5\), quanto maior for o valor de \(n\), menor será o resultado de \(0,5^n\), onde em um certo momento esse resultado será tão pouco significante que iremos "considerar" que é igual a zero.

Dessa forma, a expressão para a soma infinita é:

\[ S_{ \infty } = \dfrac{a_1 \left( q^n - 1 \right)}{q-1} \\ S_{ \infty } = \dfrac{a_1 \left( 0 - 1 \right) }{q-1} \\ S_{ \infty } = \dfrac{- a_1}{q-1} \\ S_{ \infty } = \dfrac{a_1}{1-q} \]

👉 Leia também

Matemática no Enem 2024: assuntos que mais caem na prova

Geometria analítica: o que é, principais conceitos e fórmulas

Geometria plana: principais conceitos, fórmulas e exercícios

Curiosidade: você aceitaria um salário de um centavo?

No início dessa publicação, mencionamos um emprego que o salário inicial seria de um centavo e que, a cada mês, o seu salário iria dobrar. Com todo o conhecimento que você tem agora sobre progressões geométricas, você aceitaria esse emprego?

Você pode estar pensando que não vale muito apena essa proposta e, de fato, inicialmente o salário é muito pequeno. Porém, se você der tempo ao tempo, seu salário irá alcançar proporções inimagináveis.

Confira abaixo qual seria o seu salário após dois anos (ou 24 meses) de trabalho:

\[ a_{24} = 0,01 \cdot 2^{23} = 0,01 \cdot 8 388 608 = \text{ R\$ } 83 886, 06\]

Nada mal receber mais que R$ 80 mil por mês, não é mesmo?

É claro que essa situação é totalmente hipotética e, constitucionalmente, seria impossível contratar qualquer pessoa com um salário inicial de um centavo. O valor é quase nada, mas, mês após mês, a constância pode ganhar proporções gigantescas.

Resumo: progressão geométrica

Bastante conteúdo, não é mesmo? Então vamos sintetizar tudo que estudamos!

• Uma progressão geométrica é uma sequência numérica onde o próximo valor da progressão é dado pelo produto de um valor constante, que denominamos por razão \(q\) com o valor do termo antecessor: \[ a_n = a_{n-1} \cdot q \]
• Como consequência dessa primeira formulação, temos a fórmula geral do termo da PG, que é dada pela expressão: \[ a_n = a_1 \cdot q^{n-1} \]
• As progressões geométricas podem ser classificadas como crescentes, quando a sua razão \(q\) for maior do que \(1\); decrescente, quando a razão \( q \) satisfaz \( 0 < q < 1 \), constante quando a razão for igual a \(1\) e alternada quando a potência for negativa.
• Quando a progressão geométrica é finita, usamos a expressão \[ S_n = \dfrac{a_1 \cdot \left( q^n - 1 \right)}{q - 1} \]
• Para as progressões geométricas de infinitos termos, quando \( -1 < q < 1, \text{ e } q \neq 0\), temos a expressão \[ S_{ \infty } = \dfrac{a_1}{1-q} \]

Como a PG cai no Enem e vestibulares

Se você está na preparação para o ingresso na universidade, pode fazer isso se preparando para os vestibulares ou para o Enem. Assim, entender a diferença entre essas provas é crucial para direcionar seus estudos e garantir a aprovação.

Os vestibulares costumam cobrar progressões geométricas de uma forma mais técnica e teórica, exigindo que o aluno tenha conhecimento das propriedades, fórmulas e aplicações em contextos menos contextualizados e mais diretos ao ponto.

Já o Enem costuma cobrar questões de progressões geométricas de uma forma bem contextualizada com algum problema do cotidiano ou alguma situação geométrica. Dessa maneira, o exame exige a habilidade de identificar padrões e aplicar a multidisciplinaridade.

Apesar do Enem cobrar de uma forma menos teórica os conteúdos, e em particular as progressões, nada o impede de colocar uma questão mais técnica. Na edição do Enem 2023, por exemplo, tivemos uma questão bem interessante abordando as propriedades e conhecimentos sobre progressões geométricas:

Exemplo de progressão geométrica no Enem

(Enem 2023) O esquema mostra como a intensidade luminosa decresce com o aumento da profundidade em um rio, sendo L₀ a intensidade na sua superfície.

Considere que a intensidade luminosa diminui, a cada metro acrescido na profundidade, segundo o mesmo padrão do esquema.

A intensidade luminosa correspondente à profundidade de 6 m é igual a

a) \( \dfrac{1}{9} L_0 \)

b) \( \dfrac{16}{27} L_0 \)

c) \( \dfrac{32}{243} L_0 \)

d) \( \dfrac{64}{729} L_0 \)

e) \( \dfrac{128}{2187} L_0 \)

Resposta: [D]
A sequência de intensidades luminosas corresponde a uma progressão geométrica de razão \( \dfrac{2}{3} \). 

Sendo assim, a intensidade luminosa correspondente à profundidade de 6 m (sétimo termo da PG) é igual a:

\[ \begin{eqnarray} a_n &=& a_1 \cdot q^{n-1} \\ a_7 &=& L_0 \cdot \left( \dfrac{2}{3} \right)^{7-1} \\ a_7 &=& L_0 \cdot \dfrac{2^6}{3^6} \\ a_7 &=& \dfrac{64}{729} \cdot L_0 \end{eqnarray} \]

Exemplo de progressão geométrica nos vestibulares

(Fuvest 2024) Uma Árvore Pitagórica é uma figura plana que é construída por etapas. Na Etapa 1, ela começa com um quadrado de lado 1 cm. Na Etapa 2, constroem-se dois quadrados acima do quadrado da Etapa 1, de tal forma que a medida de seus lados seja igual à medida dos catetos do triângulo retângulo isósceles que possui hipotenusa igual ao lado do quadrado da Etapa 1. Na Etapa 3, aplica-se a Etapa 2 em cada um dos novos quadrados obtidos, e assim por diante. Ou seja, em cada nova etapa, aplica-se a etapa anterior em cada um dos novos quadrados obtidos. A figura a seguir exibe as quatro primeiras etapas da construção da Árvore Pitagórica.

A partir de qual etapa da construção o lado de cada um dos novos quadrados obtidos fica, pela primeira vez, menor do que 1 décimo de milésimo do lado do quadrado da Etapa 1?

Note e adote: \( log_{10}(2) = 0,3 \)

a) 26

b) 27

c) 28

d) 29

e) 30

Resposta: [C]
A partir de um quadrado de lado L, é formado um triângulo de lado: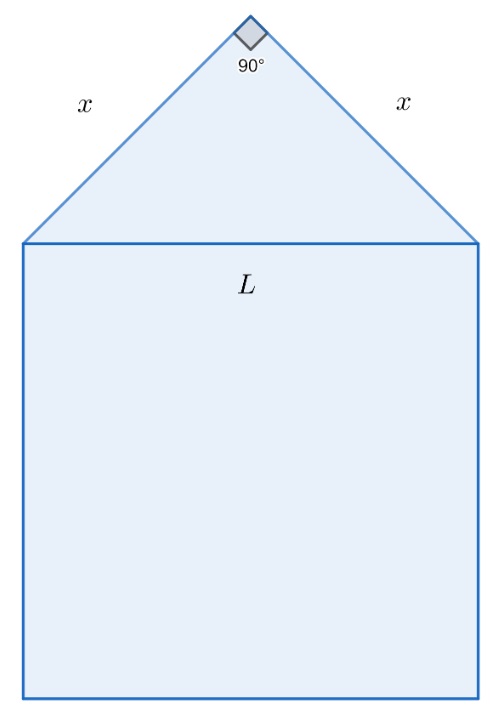



\[ \begin{eqnarray} L^2 &=& x^2 + x^2 \\ L^2 &=& 2x^2 \\ x &=& \dfrac{L}{\sqrt{2}} \end{eqnarray} \]
Ou seja, os lados dos triângulos formados são termos de uma progressão geométrica de razão \(\dfrac{1}{\sqrt{2}} = 2^{-\frac{1}{2}} \). Dessa forma, devemos ter:

\[ \begin{eqnarray} a_1 \cdot q^{n-1} &\leq & \dfrac{1}{10} \cdot \dfrac{1}{1000} \\ 1 \cdot \left( 2^{-\frac{1}{2}} \right)^{n-1} &\leq & \dfrac{1}{10000} \\ 2^{-\frac{n-1}{2}} &\leq & 10^{-4} \\ log \left( 2^{-\frac{n-1}{2}} \right) &\leq & log \left( 10^{-4} \right)  \\ -\dfrac{n-1}{2} \cdot log(2) &\leq & -4 \cdot log(10) \\ \dfrac{n-1}{2} \cdot 0,3 &\geq & 4 \\ n &\geq & 27,666 \dots \end{eqnarray} \]
Dessa forma, a partir da 28ª etapa da construção o lado de cada um dos novos quadrados obtidos fica, pela primeira vez, menor do que 1 décimo de milésimo do lado do quadrado da Etapa 1. Portanto, resposta C.

🥇 Quer se preparar para o Enem e vestibulares com quem mais entende do assunto? A plataforma Aprova Total é a maior especialista no ensino digital e tem as melhores videoaulas e professores!