Geometria analítica: o que é, principais conceitos e fórmulas
Entenda como funciona essa área da Matemática que estuda formas e princípios geométricos sob a perspectiva da álgebra, e saiba como esse assunto aparece no Enem e vestibulares

Acessibilidade
A geometria analítica é a responsável pelo estudo de pontos, retas e circunferências, através de equações e representações analíticas sobre os elementos da geometria plana e espacial.
A palavra "analítica" traz um sentido de que os elementos possuem "endereço". Isso é, na geometria analítica, a posição - ou coordenadas - é muito importante e conseguimos diferenciar pontos através de sua estrutura algébrica. Já na geometria plana, a posição em que o ponto se encontra é irrelevante, pois é baseada em axiomas (verdades matemáticas absolutas).
Para entender a fundo como isso funciona, aperte os cintos e embarque nessa aventura interdisciplinar entre geometria e álgebra. A seguir, vamos estudar as propriedades dos objetos geométricos, a aplicação dos conceitos, equações e fórmulas, e resolver os exercícios dos principais vestibulares e do Enem. Vamos nessa?
NAVEGUE PELOS CONTEÚDOS
O que é geometria analítica? Como ela é dividida?
A geometria analítica é uma subárea da álgebra linear que se responsabiliza pelo estudo analítico dos objetos geométricos como retas, pontos e planos.
Também conhecida como geometria de coordenadas, é um ramo da matemática que combina a álgebra linear e a geometria euclidiana. Essa fusão permite o estudo de figuras geométricas usando um sistema de coordenadas e os princípios da álgebra e do cálculo. Ao fazer isso, ajuda a analisar e resolver problemas geométricos.

Diferente da geometria plana e espacial, onde estudamos os mesmos objetos com uma abordagem axiomática (através de teoremas, postulados e axiomas), na geometria analítica, fazemos o estudo voltado às coordenadas de cada ponto, o que faz com que essa geometria seja muito mais "contas".
Conceitos fundamentais de geometria analítica
Assim como tudo na Matemática, precisamos de conceitos muito bem definidos para a construção teórica. E na geometria analítica, não é diferente! Por isso, vamos apresentar os principais conceitos dessa área.
Plano Cartesiano
O plano cartesiano tem como origem o produto cartesiano (o que justifica o seu nome) entre os conjuntos dos reais \( \mathbb{R} \times \mathbb{R} = \mathbb{R}^2 \). Sua estrutura é formada por duas retas perpendiculares que definimos como os eixos reais.
Esses dois eixos irão dividir nosso plano cartesiano em quatro partes, que chamamos de quadrantes. Como elementos desse plano, temos os pontos \( (x_0, y_0) \), onde \( x_0 \in \mathbb{R} \) (no primeiro conjunto real) e \( y_0 \in \mathbb{R} \) (no segundo conjunto real).
Cada entrada dos pontos se chama coordenadas e dizemos que \( x_0 \) pertence ao eixo das abscissas \(x\) e \( y_0 \) pertence ao eixo das ordenadas \(y\).
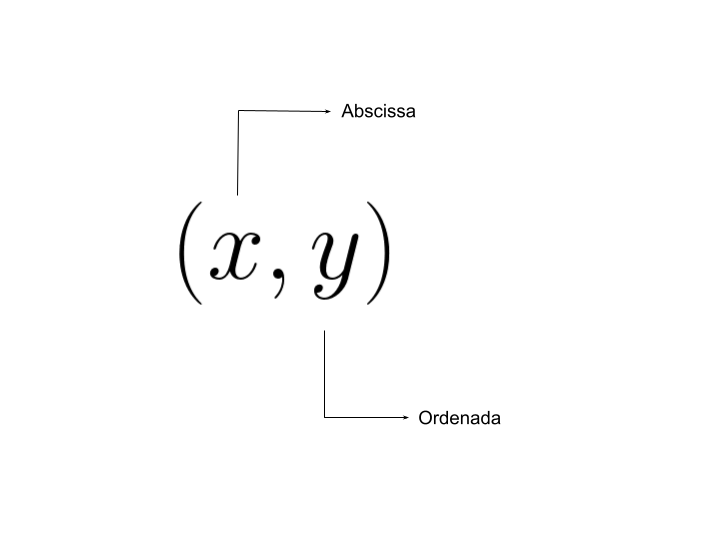
Outra base muito importante é a \( \mathbb{R}^3 \) que daremos o nome de espaço. Sua construção é dada ao inserirmos uma dimensão no plano cartesiano que já estudamos, o que nos abre um leque de possibilidades de formas, posições e propriedades.
Temos agora os eixos \(x\) e \(y\) que já estamos habituados, e também o eixo \(z\) que nos dará a noção de volume, conhecido como eixo das cotas.
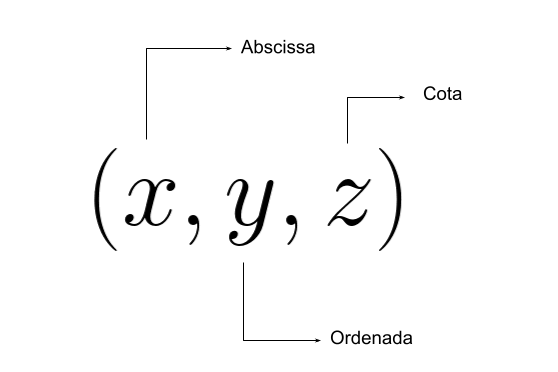
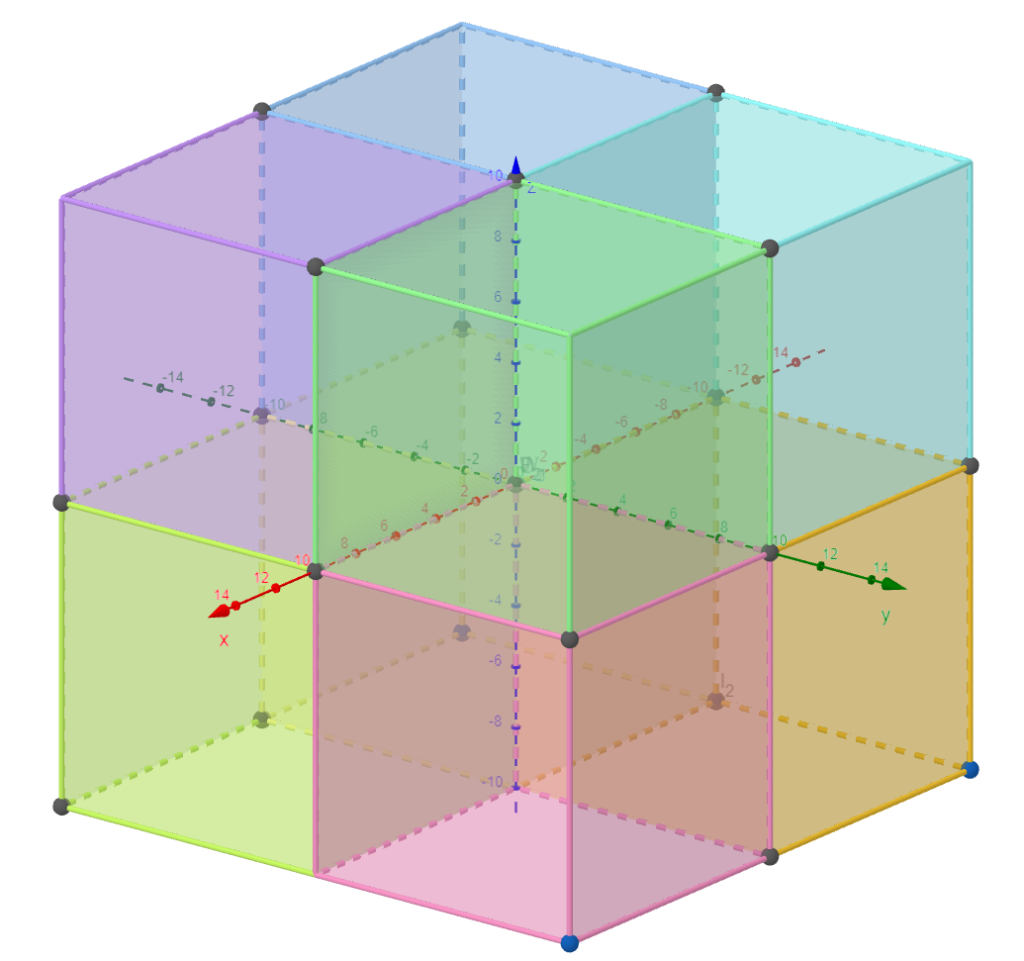
Anteriormente, no plano cartesiano, nossos eixos dividiam o plano em quatro partes das quais chamamos de quadrantes. Agora, os eixos irão dividir o espaço em oito partes onde cada uma será chamada de octante.
Coordenadas cartesianas
Como explicamos acima, cada ponto tem suas coordenadas que pertencem a cada eixo correspondente. Como cada coordenada é um valor real \( (\mathbb{R}) \), existem três possibilidades para cada entrada:
- positiva: \( x_0 > 0\);
- nula: \(x_0 = 0\);
- negativa: \(x_0 < 0\).
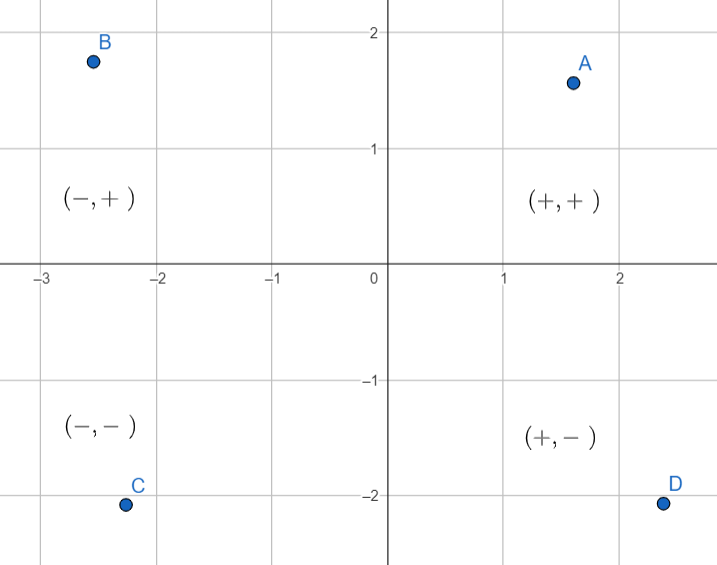
Cada valor de \(x\) ou de \(y\) irá nos dizer em qual dos quadrantes nosso ponto se encontra.
- Se \(x_0, y_0 > 0\), então o ponto está no primeiro quadrante.
- Se \(x_0 < 0, y_0 > 0\) então o ponto está no segundo quadrante.
- Se \(x_0, y_0 < 0\), então o ponto está no terceiro quadrante.
- Se \(x_0 > 0, y_0 < 0\) então o ponto está no quarto quadrante.
Mas e se uma das coordenadas for exatamente igual a zero? Bom, nesse caso, isso significa que nosso ponto não está em nenhum quadrante, mas sim em cima de um os eixos.
Se a coordenada \(x\) for nula, então ele estará sobre a reta \(y\). E caso \(y\) seja igual a zero, nosso ponto se encontra no eixo \(x\). Observe a imagem abaixo que descreve o que falamos.
Ponto
O ponto é uma estrutura primária, elemento do produto cartesiano \( \mathbb{R} \times \mathbb{R} = \left\{ (x, y) \text{ tal que } x, y \in \mathbb{R} \right\} \). É um elemento adimensional, ou seja, não possui dimensão.
Se você analisar a aparência da representação de um ponto, terá um círculo, que por sua vez possui duas dimensões (altura e largura), correto? Mas que fique claro que o ponto em si não tem dimensão, porém não conseguimos desenhar algo sem dimensão. Por isso, essa representação é feita por meio de círculos.
🎲 Nos próximos tópicos, iremos demonstrar como a união de vários pontos pode formar figuras que possuem dimensões.
Vetor
Agora que já sabemos o que são pontos e sua estrutura, somos capazes de construir vetores. Um vetor é um objeto geométrico que possui três características:
- Norma: um tamanho que pode representar uma força ou uma distância;
- Direção: responsável por dizer para qual caminho uma partícula se move;
- Sentido: em um sentido de direção, o ponto pode se mover para a "direita" ou "esquerda".

Dados dois pontos distintos \( A (x_0, y_0), B(x_1, x_2) \), definimos o vetor \( \vec{AB} \) pela diferença entre os pontos \( \vec{AB} = B - A = ( x_1 - x_0, y_1 - y_0) \). Outra notação muito comum na literatura é a notação em letras minúsculas \( \vec{u} \).
Reta
Da geometria plana, temos que por dois pontos passam uma única reta, o que é verdade independentemente da abordagem. Porém, na geometria analítica, conseguimos caracterizar a reta em forma de conjunto:
\[ r = \left\{ X \in \mathbb{R}^2 | X = A + \lambda \cdot \vec{AB} \right\}, \lambda \in \mathbb{R} \]
A expressão \( X = A + \lambda \cdot \vec{AB} \) é a equação vetorial da reta, mas leia matematicamente o que significa essa equação! Nosso \(X\) é um ponto do plano cartesiano, assim como \(A\), onde \(A\) é o ponto inicial de nossa reta, \( \vec{AB} \) é chamado vetor diretor de nossa reta e \( \lambda \) é o parâmetro que irá variar para que \(X\) seja, de fato, um ponto da reta.
A partir dessa equação, definiremos outras três equações da reta que são muito importantes.
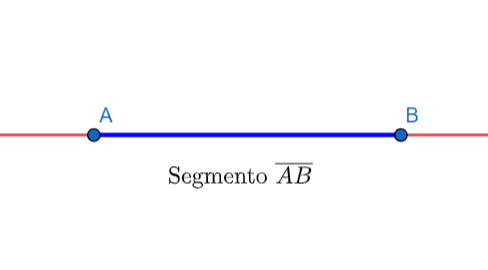
Segmento de reta
Sabemos que um segmento é apenas um pedaço da reta delimitado entre dois pontos. De forma analítica, podemos definir o segundo conjunto:
\[ \overline{AB} = \left\{ X \in \mathbb{R}^2 | X = A + \lambda \cdot \vec{AB}, \lambda \in [0, 1] \right\} \]
Como você pode observar, pouca coisa se alterou da equação da reta para a equação do segmento, afinal, um segmento é um pedaço da reta. A única diferença é que nosso parâmetro \(\lambda\) está limitado entre zero e um. Dessa forma, obteremos apenas o segmento que começa em \(A\) e termina em \(B\).
👉 Leia também
Matemática no Enem: o que você deve saber para ir bem na prova
Vença o medo da Matemática com essas dicas de estudo
Distância entre dois pontos
Já sabemos que por dois pontos, podemos determinar um vetor. Estamos agora interessados apenas em seu tamanho. Observe, na figura abaixo, que para calcular a distância entre dois pontos, iremos nos ater à coordenada de cada um deles. Assim, temos uma espécie de triângulo retângulo.
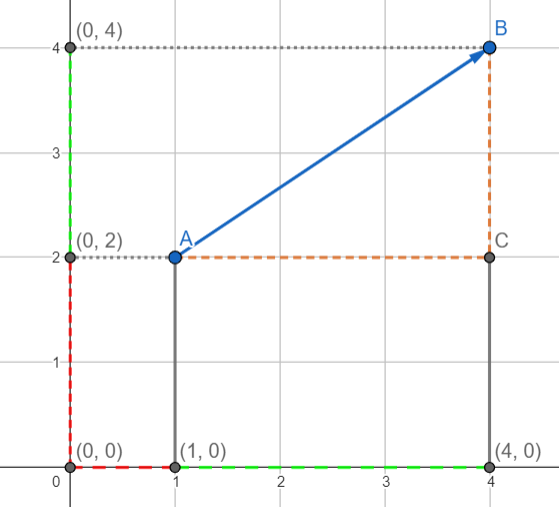
Pelo teorema de Pitágoras, sabemos que o quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
\[ a^2 = b^2 + c^2 \\ \\ a = \sqrt{b^2 + c^2} \]
Feita essa analogia, temos que \( a = || \vec{AB} || = d(A, B), b = x_1 - x_0, c = y_1 - y_0 \), e assim
\[ d(A, B) = \sqrt{(x_1 - x_0)^2 + (y_1 - y_0)^2} \]
Mas não queremos ver você simplesmente decorando fórmulas, vamos pensar juntos e ler matematicamente a equação acima. A distância entre dois pontos precisa passar pelos seguintes passos:
- Encontrar o vetor \( \vec{AB} \);
- Calcular o quadrado das coordenadas de \( \vec{AB} \);
- Somar o valor dos quadrados das coordenadas;
- Calcular a raiz dessa soma.
Dessa forma, temos uma maneira geral de calcular distâncias sem ficarmos presos à notação e à "decoreba".
Equação fundamental da reta
Uma equação muito importante é a equação fundamental da reta, que será muito presente também nas funções do primeiro grau. Veja:
\[ y - y_0 = m \cdot (x - x_0) \]
Onde \( (x_0, y_0) \) é o ponto inicial de nossa reta e \(m\) um número real que nos diz o quão inclinada nossa reta se encontra. Mais ainda, conseguimos escrever uma expressão para \(m\). Considere \( (x_0, y_0), (x_1, y_1) \) pontos distintos que pertencem à reta, então \(m\) será dado pela expressão
\[ m = \dfrac{y_1 - y_0}{x_1 - x_0} \]
Não que seja uma coincidência, mas você se recorda quando falamos sobre a distância entre pontos que poderíamos construir um triângulo retângulo com a "sombra" do segmento definido entre dois pontos
Se você reparar, \(y_1 - y_0 \) é o tamanho do cateto oposto e \(x_1 - x_0\), o cateto adjacente. Assim, a tangente do ângulo é dada por
\[ tg(\alpha ) = \dfrac{\text{cat. oposto}}{\text{cat. adjacente}} \\ \Rightarrow m = tg(\alpha ) \]
Isso não é uma coincidência, justamente pela formação do triângulo retângulo da projeção dos pontos em seus eixos coordenados.
Coeficiente angular
O \(m\) que definimos anteriormente é conhecido como coeficiente angular, ou seja, uma constante que define o ângulo que a reta forma com os eixos, mais especificamente o eixo \(x\). E assim, temos três possibilidades:
- \( m > 0 \rightarrow \) a reta será crescente;
- \( m = 0 \rightarrow \) a reta será constante;
- \( m < 0 \rightarrow \) a reta será decrescente.
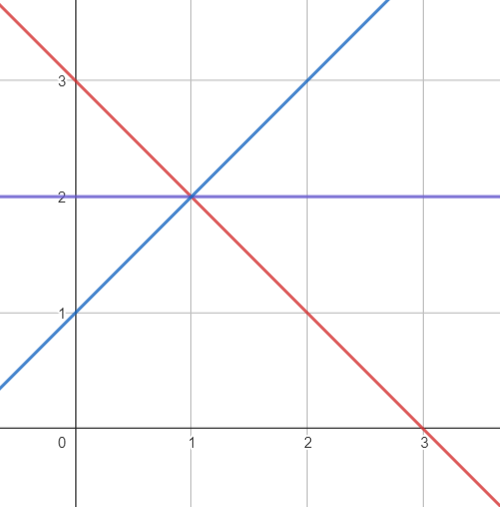
Posições relativas
Como cada reta e plano possuem posições e inclinações diferentes, cada um desses casos nos gera propriedades interessantes. Vamos ver juntos quais são elas?
Entre planos
Entre dois planos, temos as seguintes possibilidades de posições:
- planos concorrentes, que sempre irão se encontrar formando um reta;
- planos paralelos, em que ainda temos a possibilidade de planos diferentes ou coincidentes.

Entre retas
Para a posição entre duas retas, temos os seguintes casos:
- Paralelas: assim como os planos paralelos, temos a possibilidade delas serem diferentes, ou seja, não terem pontos em comum, ou serem coincidentes, e assim, todos os pontos são comuns.
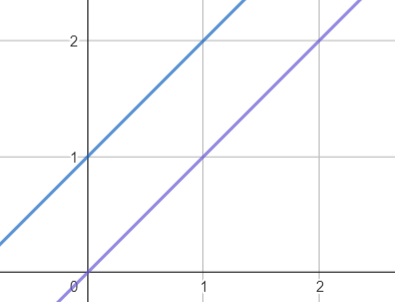
- Transversais: quando não são paralelas, dizemos que as retas são concorrentes, o que irá gerar dois casos. As concorrentes, quando as retas possuem apenas um ponto em comum, e as reversas, retas transversais que não possuem pontos em comum.
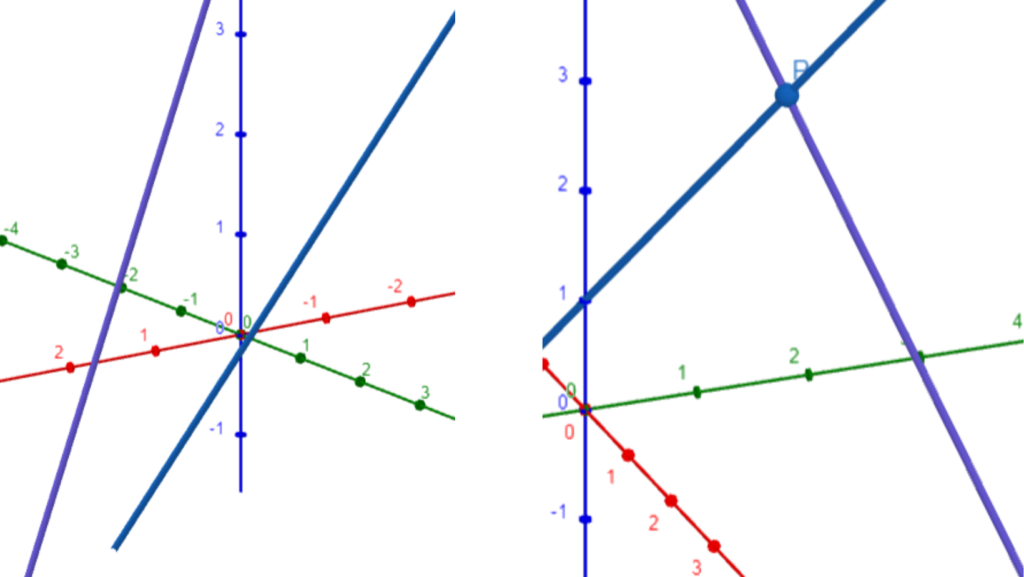
Entre ponto e reta
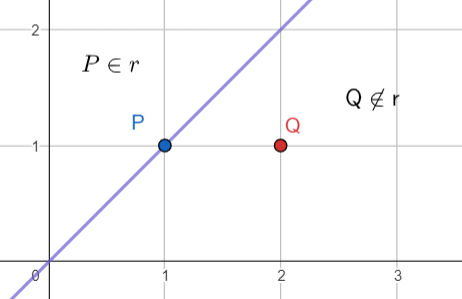
Quando falamos em posições relativas entre reta e ponto, temos apenas duas possibilidades:
- o ponto pertence a reta, ou seja, suas coordenadas satisfazem a equação fundamental da reta;
- o ponto não pertence a reta e, no caso, não irá satisfazer a equação fundamental da reta.
Principais fórmulas da Geometria Analítica
Traremos aqui as principais fórmulas (de forma resumida) para que você tenha sempre em mãos quando estiver estudando. Vale até fazer uma nota autoadesiva, beleza? 📝
Fórmulas de distância
- Distância entre dois pontos \(A(x_1, y_1)\) e \(B(x_2, y_2)\): \( d(A, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \);
- Distância entre ponto e reta \(A(x_1, y_1)\) e \( r: ax + by + c = 0\): \( \dfrac{| x_1 \cdot a + y_1 \cdot b |}{\sqrt{a^2 + b^2}} \)
Equação da reta
- Equação fundamental da reta: \( y - y_0 = m \cdot (x - x_0) \), onde \( m = \dfrac{y_1 - y_0}{x_1 - x_0} \)
- Equação geral da reta: \( ax + by + c = 0 \)
- Equação vetorial: \( X = A + \lambda \cdot \vec{AB} \)
- Equação paramétrica: \( \begin{cases} x = x_0 + \lambda \cdot u \\ y = y_0 + \lambda \cdot v \end{cases} \)
- Equação paramétrica: \( \dfrac{x - x_0}{u} = \dfrac{y - y_0}{v} \)
Fórmulas de cônicas
- Circunferência: \( (x - x_0)^2 + (y - y_0)^2 = r^2 \)
- Elipse: \( \dfrac{(x - x_0)^2}{a^2} + \dfrac{(y - y_0)^2}{b^2} = 1 \) ou \( \dfrac{(x - x_0)^2}{b^2} + \dfrac{(y - y_0)^2}{a^2} = 1 \)
- Parábola: \( (x - x_0)^2 = 2p(y - y_0) \) ou \( (y - y_0)^2 = 2p(x - x_0) \)
- Hipérbole: \( \dfrac{(x - x_0)^2}{a^2} - \dfrac{(y - y_0)^2}{b^2} = 1 \) ou \( \dfrac{(x - x_0)^2}{b^2} - \dfrac{(y - y_0)^2}{a^2} = 1 \)
👉 Leia também
Dicas fundamentais para interpretar gráficos e tabelas
Medidas de tendência central: o que são e como caem no Enem
Circunferência, parábola e cônicas
Outra grande área de estudos da geometria analítica são as famosas cônicas e, aqui, encontraremos circunferências, parábolas, elipses e hipérboles. De forma geral, cada uma dessas figuras se chama lugar geométrico, que é basicamente o conjunto que satisfaz alguma condição geométrica.
Circunferência
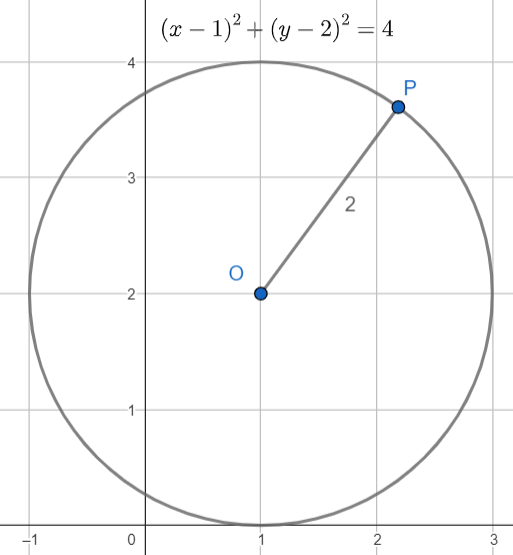
A circunferência é o lugar geométrico dos pontos equidistantes de um ponto \(O\). Sim, parece confuso, mas vem com a gente, pois nós vamos dar mais sentido para essa frase!
Considere um ponto \( O(0,0) \) a origem do nosso plano cartesiano e considere uma distância \(d = 5 \). Observe que o ponto \( (5, 0) \) satisfaz essa distância, o que significa que ele pertence ao lugar geométrico da circunferência.
Agora, \( (5, 0) \) é o único ponto que satisfaz essa distância? Não mesmo! Todos os pontos que satisfizerem a equação abaixo pertencerão ao lugar geométrico da circunferência.
\[ x^2 + y^2 = 5^2 \]
De forma geral, para uma distância \(d\), o lugar geométrico da circunferência será os pontos que satisfazem a equação
\[ (x - x_0)^2 + (y - y_0)^2 = d^2 \]
Onde \( (x_0, y_0) \) é o centro de nossa circunferência e \(d\) será o raio de nossa circunferência.
Elipse
Temos agora um lugar geométrico que é muito semelhante à circunferência, porém um pouco "achatado". Estamos falando da elipse, onde agora não teremos um ponto central, mas dois pontos, que chamaremos de focos da elipse. Esses focos serão fundamentais para a construção do lugar geométrico da elipse.
Para a circunferência, o lugar geométrico eram os pontos com distância constante do centro. Agora, na elipse, temos uma ideia semelhante, porém em relação aos dois focos que mencionamos anteriormente.
Uma observação interessante a se fazer é que a elipse é obtida por um corte perpendicular a um cone agudo.
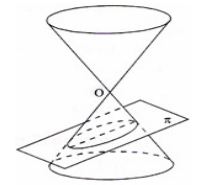
A elipse é o conjunto de todos os pontos para os quais a soma das distâncias a dois pontos fixos, chamados focos, é constante.
Vamos agora aos elementos da elipse:
- \( F_1\) e \(F_2\) são os focos da elipse que se encontram no maior eixo;
- Vértice da parábola são os dois pontos com maior distância entre si;
- Um ponto \(P\) que pertence à circunferência satisfaz à seguinte propriedade
\[ d(P, F_1) + d(P, F_2) = 2a \]
onde \(a>0\) é a distância dos vértices do eixo menor aos focos da elipse;
- A distância entre os focos é dada por \( d(F_1, f_2) = 2c \), com \(c>0\)
- O eixo menor mede 2b e é determinado pelos pontos \(B_1\) e \(B_2\)
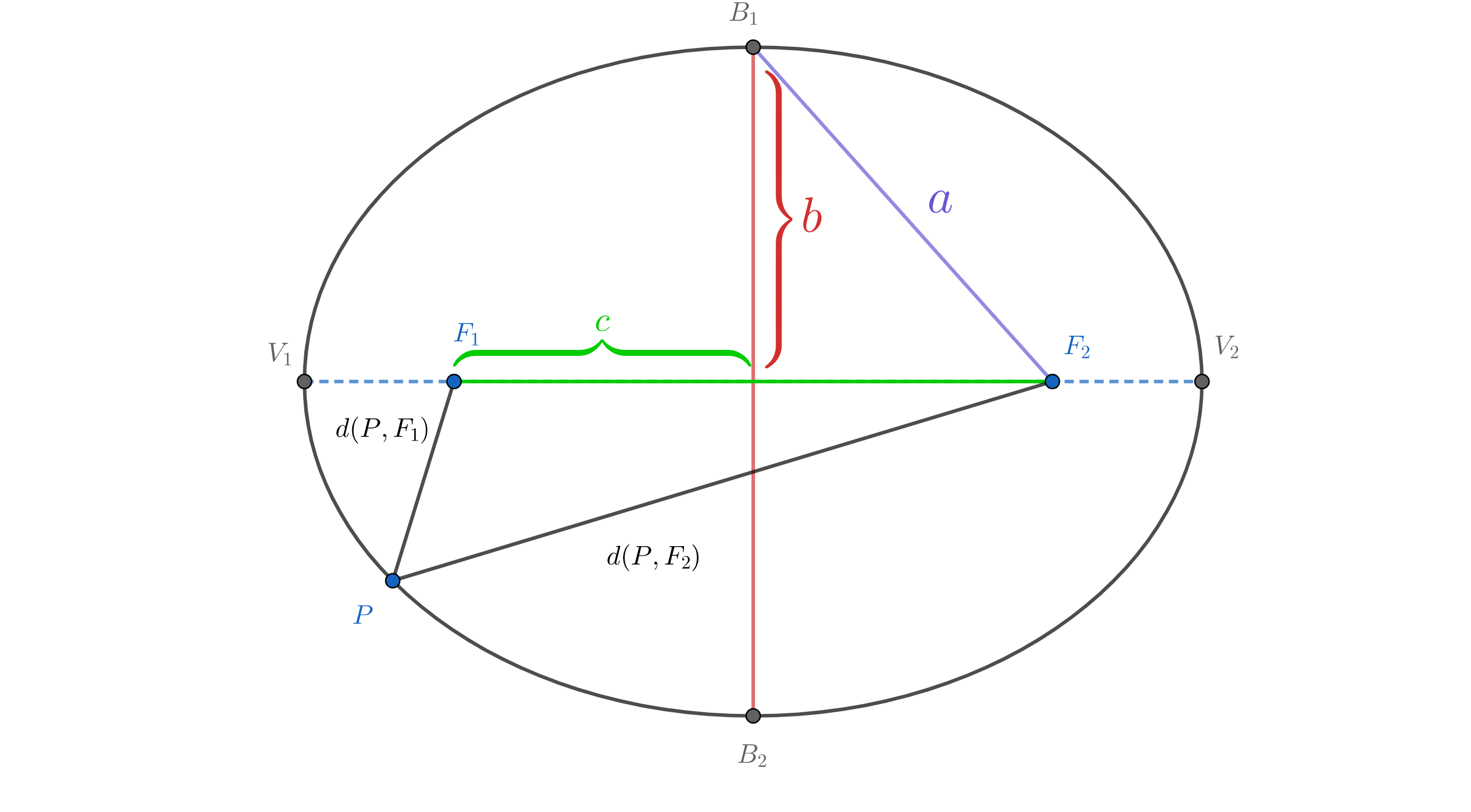
A equação reduzida da elipse, quando o eixo maior é paralelo ao eixo \(x\) é dada por
\[ \dfrac{(x- x_0)^2}{a^2} + \dfrac{(y-y_0)^2}{b^2} = 1 \]
Já quando o eixo maior é paralelo ao eixo \(y\), a equação reduzida da elipse é dada por
\[ \dfrac{(x- x_0)^2}{b^2} + \dfrac{(y-y_0)^2}{a^2} = 1 \]
Onde \( (x_0, y_0) \) é o centro da elipse.
Parábola
A parábola, muito estudada em funções do segundo grau, é o lugar geométrico dos pontos que estão equidistantes de um ponto fixo \(F\) (o foco) e de uma linha reta fixa \(d\) (a diretriz).
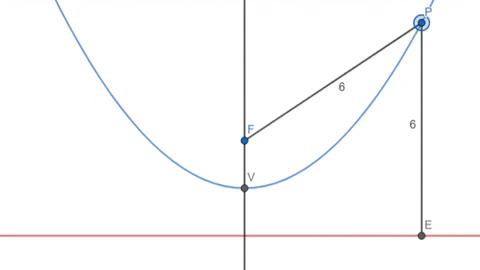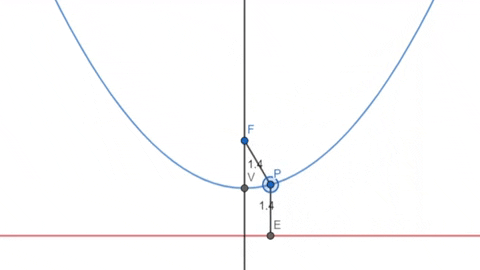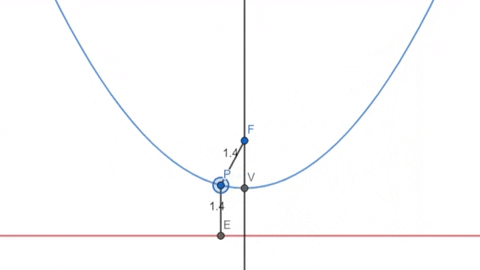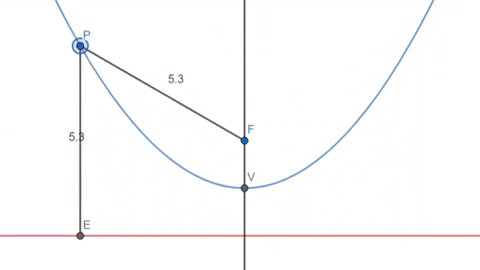
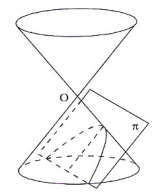
Assim como a elipse, podemos obter uma parábola cortando de forma perpendicular um cone reto.
Diferente da função do segundo grau, onde a equação precisa satisfazer as condições de funções, na geometria analítica, não temos essa necessidade, podemos ter:
- parábolas em pé, quando a reta diretriz é paralela ao eixo \(x\);
- deitadas, quando a reta diretriz é paralela ao eixo \(y\);
- e ainda parábolas oblíquas, quando a reta diretriz não é paralela a nenhum dos eixos.
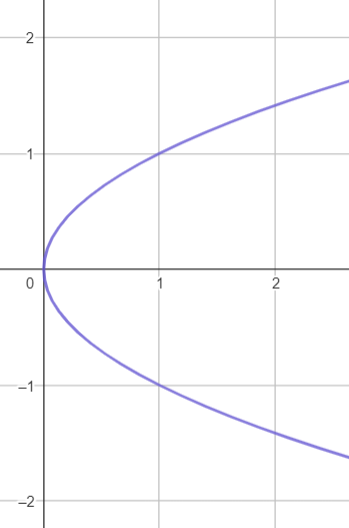
De forma geral, a equação reduzida da parábola é dada por:
- Diretriz paralela ao eixo \(y\):
- Foco à direita da diretriz: \( (y-y_0)^2 = 4p(x-x_0) \)
- Foco à esquerda da diretriz: \( (y-y_0)^2 = -4p(x-x_0) \)
- Diretriz paralela ao eixo \(x\):
- Foco acima da diretriz: \( (x-x_0)^2 = 4p(y-y_0) \)
- Foco abaixo da diretriz: \( (x-x_0)^2 = -4p(y-y_0) \)
Onde \(p\) é o ponto médio entre o foco \(F\) e a diretriz \(d\). Nesse ponto médio, encontra-se o vértice da parábola.
- Quando seu vértice tem coordenadas \( \left( x_v, y_v \right) \), o foco e diretriz serão \( F = \left( x_v \pm p, y_v \right) \) e a reta diretriz \( d: x = \mp p\);
- quando a diretriz \(d\) for paralela ao eixo \(x\) e ainda, \( F = \left( x_v, y_v \pm p \right) \) e a reta diretriz \( d: y = \mp p\), quando a diretriz \(d\) for paralela ao eixo \(y\).
Hipérbole
Por último, mas não menos importante, temos a hipérbole, figura gerada ao cortarmos um cone em suas duas folhas. Até agora, essa é a figura mais "diferente" das demais, por ter dois pedaços, ser aberta e possuir algo que nenhuma forma geométrica teve até agora, que são assíntotas.
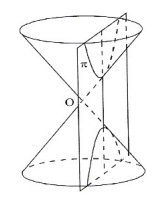
O lugar geométrico dos pontos do plano cujo valor absoluto da diferença de suas distâncias a dois pontos fixos \(F_1\) e \(F_2\) é constante e igual a \(2a\ , a > 0\), é uma hipérbole. Os pontos \(F_1\) e \(F_2\) são denominados focos.
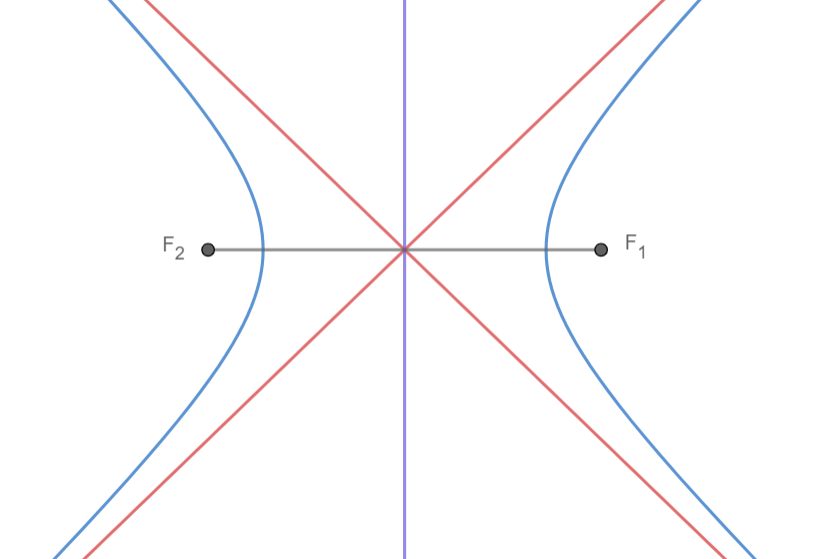
Onde \(F_1, F_2\) são os focos:
- o segmento cinza é o eixo principal, que contém os focos;
- a reta roxa é o eixo conjugado, que nos dá o eixo de simetria da hipérbole;
- as retas vermelhas são as assíntotas, retas que "guiam" a hipérbole e a limitam, de forma que a hipérbole nunca cruze ou toque a assíntota.
Como o eixo dos focos pode ser paralelo tanto ao eixo \(x\) como ao eixo \(y\), temos duas equações que descrevem nossa hipérbole:
- Quando o eixo principal é paralelo ao eixo \(x\)
\[ \dfrac{(x-x_0)^2}{a^2} - \dfrac{(y-y_0)^2}{b^2} = 1 \]
- Quando o eixo principal é paralelo ao eixo \(y\)
\[ \dfrac{(y-y_0)^2}{a^2} - \dfrac{(x-x_0)^2}{b^2} = 1 \]
Resumo: geometria analítica
Bastante coisa, não é mesmo? 😅 Mas não se preocupe! Para ajudar você a ficar fera e dominar esse conteúdo, a gente fez um resumo de geometria analítica. Confira!
Ponto
Objeto geométrico que pertence ao produto cartesiano \( \mathbb{R} \times \mathbb{R} \). Com mais de um ponto podemos calcular distâncias, formar retas, definir regiões, e a distância entre dois pontos \(A(x_1, y_1)\) e \(B(x_2, y_2)\) é dada por
\[ d(A, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Retas
As retas são um conjunto de pontos colineares, a sua principal equação é dada por
\[ y - y_0 = m \cdot (x - x_0) \text{ com } m = \dfrac{y_1 - y_0}{x_1 - x_0} \]
Circunferência
Importante figura geométrica, formada pelos pontos equidistantes de um centro \( O(x_0, y_0) \). Sua equação é dada pela expressão: \[ (x -x_0)^2 + (y - y_0)^2 = r^2 \] onde \(r = d(P, 0)\).
Como a geometria analítica cai no Enem e vestibulares
Você que está estudando para o vestibular precisa estar preparado para resolver as questões de geometria analítica. Por isso, fizemos um compilado de como as principais provas costumam cobrar esse conteúdo.
No Enem, geometria analítica não pertence ao Top 5 assuntos mais frequentes, mas isso não impede de termos questões desse tipo! Na prova de 2018, por exemplo, quatro exercícios usaram os conteúdos estudados aqui. E como o Enem 2023 não teve questões sobre o assunto, é provável que, em 2024, a gente encontre alguns exercícios do tema.
Assim, para estar bem preparado, você precisa ter boas noções sobre coordenadas e as principais posições relativas, estar familiarizado com as equações das principais formas geometrias, como retas e segmentos, circunferências e as demais cônicas da geometria analítica.
Já para os grandes vestibulares, esteja preparado para encontrar questões mais técnicas, que exigem um conhecimento aprimorado das noções geométricas e das operações algébricas. Neles, costumam cair questões para encontrar pontos comuns, como retas em intersecção com a circunferência.
Exemplo 1 - Enem
(Enem 2019) Um aplicativo de relacionamentos funciona da seguinte forma: o usuário cria um perfil com foto e informações pessoais, indica as características dos usuários com quem deseja estabelecer contato e determina um raio de abrangência a partir da sua localização. O aplicativo identifica as pessoas que se encaixam no perfil desejado e que estão a uma distância do usuário menor ou igual ao raio de abrangência. Caso dois usuários tenham perfis compatíveis e estejam numa região de abrangência comum a ambos, o aplicativo promove o contato entre os usuários, o que é chamado de match.
O usuário P define um raio de abrangência com medida de 3 km e busca ampliar a possibilidade de obter um match se deslocando para a região central da cidade, que concentra um maior número de usuários. O gráfico ilustra alguns bares que o usuário P costuma frequentar para ativar o aplicativo, indicados por I, II, III, IV e V. Sabe-se que os usuários \(Q\), \(R\) e \(S\), cujas posições estão descritas pelo gráfico, são compatíveis com o usuário \(P\) e que estes definiram raios de abrangência respectivamente iguais a 3 km, 2 km e 5 km.
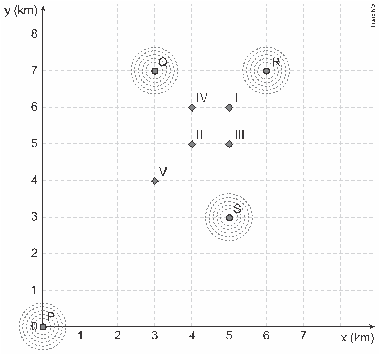
Com base no gráfico e nas afirmações anteriores, em qual bar o usuário P teria a possibilidade de um match com os usuários Q, R e S, simultaneamente?
a) I
b) II
c) III
d) IV
e) V
Resposta: [A]
Tem-se que \(Q = (3,7)\), \(R=(6,7)\), \(S=(5,3)\), \(I=(5,6)\), \(II=(4,5)\), \(III=(5,5)\), \(IV(4,6)\) e \(V =(3,4)\). Logo, como \(r_{P} = 3 km\), \(r_{Q} = 3 km\),\( r_{R}=2 km\) e \( r_{S}=5 km\) são os raios de abrangência, temos
\[ d(II,R) = 2 \sqrt{2} km > 2 km, \\ d(III,R) = \sqrt{5} km > 2 km, \\ d(IV,R) = \sqrt{5} km > 2 km, \\ d(V,R) = 3 \sqrt{2} km > 2 km \]
o que implica na escolha do bar I. Com efeito, pois \(d(I, R) = \sqrt2 km\), \(d(I, Q) = \sqrt5 km\) e \( d(I, S)=3 km\), ou seja, todos em match simultaneamente com \(P\).
Observação: \(d(M, N)\) denota a distância entre os pontos \(M=(x_M,y_M)\ e\ N=(x_N,y_N)\), de tal forma que \(d(M, N)=\sqrt{(x_M-x_N)^2+(y_M-y_N)^2}\).
Com isto, a resposta é A.
Exemplo 2 - Vestibular
(Ufsc 2023) Determine a soma dos números associados à(s) proposição(ões) correta(s).
01) Considere as retas \(r:ax+by+c_1=0\) e \(s:ax+by+c_2=0\) se \(d(r, s)\) representa a distância entre as retas \(r\) e \(s\), então \(d(r,s)=\dfrac{|c_1-c_2|}{\sqrt{a^2+b^2}}\)
02) Seja \(R\) a região do plano formada por todos os pontos cujas coordenadas satisfazem simultaneamente as inequações \(x+y \leq 0\), \(y-2 \geq 0\) e \(x+3 \geq 0\). O perímetro da região \(R\) é \(3+\sqrt{2}\).
04) Se os pontos \(A(−1,3)\) e \(B(5,1)\) são equidistantes de \(C(x, x)\), então \(x\) é ímpar.
08) Se uma parábola tem vértice na origem, eixo de simetria coincidindo com o eixo \(x\) e passa pelo ponto \(P(8,2)\), então uma equação que descreve essa parábola é \(x = 4y^2\).
16) Uma mediatriz é uma reta perpendicular a um segmento de reta e que passa pelo ponto médio desse segmento. Se a reta \(r\) é a mediatriz do segmento \(\overline{AB}\), sendo \(A(4,−1)\) e \(B(2,−7)\), então o ponto \(P(6,−5)\) pertence à reta \(r\).
32) Se os pontos \(A(5,0)\) e \(P(x, y)\) estão sobre uma elipse cujos focos são \(F_1(−3,0)\) e \(F_2(3,0)\), então o perímetro do triângulo \(PF_1F_2\) é \(16\).
Resposta: [01 + 16 + 32 = 49]
[01] Verdadeira. Da reta \(r\), obtemos:
\[ ax+by+c_1=0\Rightarrow y=-\frac{a}{b}x-\frac{c_1}{b} \]
Tomando \(x = 0\), obtemos um ponto da reta \(r\):
\[ y=-\frac{a}{b}\cdot0-\frac{c_1}{b}=-\frac{c_1}{b}\Rightarrow\left(x_r, y_r\right)=\left(0, -\frac{c_1}{b}\right) \]
Fazendo a distância deste ponto até a reta \(s\), chegamos a:
\[ d= \dfrac{\left| a \cdot 0 + b \cdot \left( -\frac{c_1}{b} + c_2 \right) \right|}{\sqrt{a^2 + b^2}} = \dfrac{\left| c_1 - c_2 \right|}{\sqrt{a^2 + b^2}}\]
[02] Falsa. O perímetro da região ilustrada na figura abaixo vale \( p=2+\sqrt{2}\)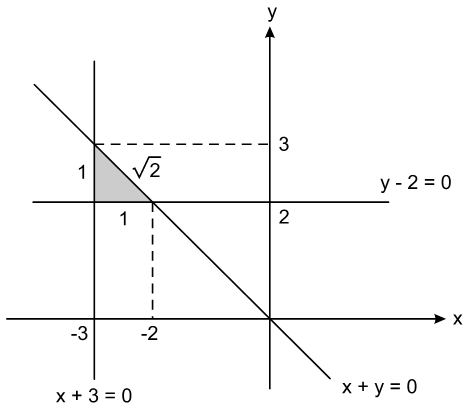
[04] Falsa. O valor de \(x\) é dado por:
\[ \begin{eqnarray} \sqrt{(x + 1)^2 + (x - 3)^2} &=& \sqrt{(x - 5)^2 + (x - 1)^2} \\ x^2 + 2x + 1 + x^2 - 6x + 9 &=& x^2 - 10x + 25 + x^2 - 2x + 1\\ 8x &=& 16 \\x &=& 2 \end{eqnarray} \]
Ou seja, \(x\) é par.
[08] Falsa. A parábola não contém o ponto P, pois:
\[ x = 4 y^2 \Rightarrow 8 = 4 \cdot 2^2 \Rightarrow 8 \neq 16 \]
Ou seja, a equação dada não pode representar a parábola descrita.
[16] Verdadeira. Ponto médio do segmento:
\[ (x_m, y_m) = \left(\frac{4+2}{2}, \frac{-1-7}{2}\right) = \left(3, -4\right) \]
Equação de \(r\):
\[ m_{AB} = \frac{-1+7}{4-2} = 3\Rightarrow m_r = -\frac{1}{3} \\ y + 4 = -\frac{1}{3} \cdot (x-3)\Rightarrow x + 3y = -9 \]
Substituindo o ponto dado:
\[ 6 + 3 \cdot (-5) = -9 \Rightarrow - 9 = - 9 \]
Logo, o ponto \(P\) pertence à reta \(r\).
[32] Verdadeira. Pela definição de elipse, temos que:
\[ \overline{PF_1} + \overline{PF_2} = \overline{AF_1} + \overline{AF_2} = 8 + 2 = 10 \]
Logo, o perímetro do triângulo vale:
\[ \overline{PF_1} + \overline{PF_2} + \overline{F_1F_2} = 10 + 6 = 16 \]
🥇 Quer se preparar para o Enem e vestibulares com quem mais entende do assunto? A plataforma Aprova Total é a maior especialista no ensino digital e tem as melhores videoaulas e professores!

