Progressão Aritmética (PA): conceitos, operações e exercícios

Progressões aritméticas são sequências numéricas importantes na Matemática. Aprenda as principais fórmulas e propriedades para aplicar nas questões do Enem e dos grandes vestibulares

11/01/2024

Oito bonecas russas azuis com cabelos loiro em sequência representando a progressão aritmética, em uma escala crescente

Acessibilidade

Considere a sequência numérica $(7, 20, 33, 46, 59, ... )$, você sabe dizer qual o próximo valor? Ou calcular a soma dos 100 primeiros termos? Esta publicação está aqui justamente para responder essas perguntas. Afinal, trata-se de uma progressão aritmética e questões assim fazem parte do estudo de sequências e progressões.

Vamos pensar em uma situação hipotética simples. Imagine que você está subindo uma escada, onde cada degrau tem a mesma altura. Cada passo que você dá é igual ao anterior, certo? Essa é a essência da progressão aritmética.

Ilustração de uma escada com degraus. Em cada degrau, um número específico, seguindo a sequência da adição do número 13. A sequência é 7, 20, 33, 46, 59 e 72.

Você começa com um número que chamamos de "termo inicial" e, a cada passo, adiciona sempre a mesma quantia isso é a "razão". É como se você estivesse caminhando com passos do mesmo tamanho. Logo, no caso da imagem acima, a cada degrau, adiciona-se a razão de valor 13.

NAVEGUE PELOS CONTEÚDOS

Progressão aritmética (PA) — definição

Progressão aritmética é uma sequência numérica onde a diferença entre cada par de termos consecutivos é sempre constante e igual à razão da PA. Esta característica faz com que a PA seja uma ferramenta fundamental em várias áreas da matemática e suas aplicações.

A representação de PA envolve uma sequência onde cada número é separado por vírgulas. Além disso, os números são comumente chamado de termos. Veja um exemplo:

A imagem representa a sequência (1, 2, 3, 4, 5, 6, 7, 8, ...). 1 é o primeiro termo. 2 é o segundo termo. ... representa que a progressão aritmética segue infinitamente

As progressões aritméticas também podem ser infinitas ou finitas:

PA Infinita - $(2,\; 4,\;6,\;8,\;...)$: possui infinitos termos.
PA Finita - $(3,\; 6,\;9,\;12)$: possui número limitado de termos.

Cada termo de uma PA é identificado pela posição que ocupa na sequência e, para representar cada termo, utilizamos uma letra (normalmente a letra a) seguida de um número que indica sua posição na sequência.

$\left(\underbrace{3}_{a_{1}},\;\underbrace{7}_{a_{2}},\;\underbrace{11}_{a_{3}},\;\underbrace{15}_{a_{4}}\right)$

Razão da PA

O valor da diferença entre quaisquer dois termos consecutivos é o que chamamos de razão da PA. Por exemplo, para encontrar a razão na PA $(4,\;7,\;10,\;13,\;16)$, devemos escolher dois termos consecutivos e subtraí-los -- lembrando que sempre deve-se utilizar o termo que está na maior posição menos o que está na menor posição. Desse modo, escolhendo $13$ e $10$, temos que $13-10=3$. Logo, a razão desta PA é 3.

A razão nem sempre é positiva. Note que na PA $(100,\;98,\;96,\;94,\;...)$, ao encontrar o valor da razão, temos que $98-100=-2$. Logo, a razão desta PA é $-2$.

Formalmente, podemos definir a razão com a seguinte expressão:

$r=a_{m+1}-a_{m},\;\;\forall m \in\mathbb{N}^*$

✅ Comumente, denotamos a razão da PA por $(r)$

Tipos de PA

Existem três tipos de progressões aritméticas e a classificação é referente ao valor que a sua razão admite. Veja abaixo a diferença entre elas.

Progressão aritmética constante

PA constante é aquela em que todos os termos são iguais. Assim sendo, sua razão é sempre igual a zero. Veja alguns exemplos de PAs constantes:

$(7,\; 7,\; 7,\; 7,\; 7,\; 7\;, …) \rightarrow r = 0$

$(100,\; 100,\; 100,\; 100,\; 100,\; 100\;, …) \rightarrow r = 0$

$(0,\; 0,\; 0,\; 0,\; 0,\; 0) \rightarrow r = 0$

Progressão aritmética crescente

PAs crescentes são todas aquelas em que os termos aumentam de tamanho à medida que a posição deles aumenta. Dessa forma, sua razão é maior que zero. Em outras palavras, a razão é positiva. Veja alguns exemplos de PAs crescentes:

$(1,\; 2,\; 3,\; 4,\; 5,\; 6\;, …) \rightarrow r = 1$

$(7,\; 10,\; 13,\; 16,\; 19,\; 22\;, …) \rightarrow r = 3$

$(100,\; 200,\; 300,\; 400,\; 500,\; 600\;, …) \rightarrow r = 100$

Formalmente, dizemos que PAs crescentes satisfazem a seguinte proposição:
$a_{n}<a_{n+1},\;\forall n \in \mathbb{N}^*$

Progressão aritmética decrescente

A PA decrescente é aquela em que os termos diminuem de tamanho à medida que a posição deles aumenta. Por isso, sua razão é menor que zero. Ou seja, a razão é negativa. Veja alguns exemplos de PAs decrescentes:

$(67,\; 60,\; 53,\; 46,\; 39,\; 32\;, …) \rightarrow r = -7$

$(20,\; 10,\; 0,\; -10,\; -20,\; -30\;, …) \rightarrow r = -10$

$(1000,\; 0,\; -1000,\; -2000,\; -3000) \rightarrow r = -1000$

✅ Dizemos que PAs decrescentes satisfazem a seguinte proposição:
$a_{n}>a_{n+1},\;\forall n \in \mathbb{N}^*$

Fórmula do termo geral da PA

A fórmula do termo geral da PA é uma equação que utilizamos para encontrar o valor de algum termo quando já sabemos o valor da razão e o valor de algum outro termo.

Existem duas maneiras usuais para representar a fórmula do termo geral da PA. A primeira é utilizando como referência o primeiro termo da PA. Portanto, a fórmula é dada por:

$a_n=a_1+(n-1)\cdot r$

Onde:

$a_{1}$: primeiro termo
$a_{n}$: $n$-ésimo termo
$n$: valor da posição do $n$-ésimo termo
$r$: razão da PA

A segunda maneira que podemos representar o termo geral é utilizando um termo qualquer como referência, não necessariamente precisa ser o primeiro termo:

$a_n=a_k+(n-k)\cdot r$

A única diferença é a mudança do índice 1 na primeira fórmula, pelo $k$ na segunda. Assim sendo, podemos concluir que sabendo a razão e um termo qualquer com sua respectiva posição, podemos encontrar o valor de qualquer termo que desejarmos.

Exemplo - Fórmula do termo geral da PA

Considere a P.A. $(17,\;19,\;21,\;...)$. Deseja-se descobrir o valor do termo que se encontra na posição de número 100. Portanto, qual é este valor?

Resposta: [215]
O primeiro passo é identificar que o valor do primeiro termo é $a_{1}=17$. O próximo passo é encontrar o valor da razão desta P.A. cujo é $19-17=2$. Assim como queremos saber o valor do termo de posição número $100$, temos que $n = 100$. Então temos:

$a_1=17$
$r=2$
$n=100$

Utilizando a fórmula do termo geral $a_{n}=a_1+(n-1)\cdot r$, temos que:
${a_{100}=17+(100-1)\cdot 2}$
$a_{100}=17+(99)\cdot 2$
$a_{100}=17+198$
$a_{100}=215$

Assim, o valor do 100º termo da P.A. $(17,\;19,\;21,\;...)$ é $215$.

Probabilidade: conceitos, cálculo e exercícios resolvidos

Matemática no Enem: o que você deve saber para ir bem na prova

Propriedades das progressões aritméticas

Existem duas propriedades das progressões aritméticas, a primeira e a segunda. Entenda como funcionam e de que forma são calculadas.

Primeira propriedade

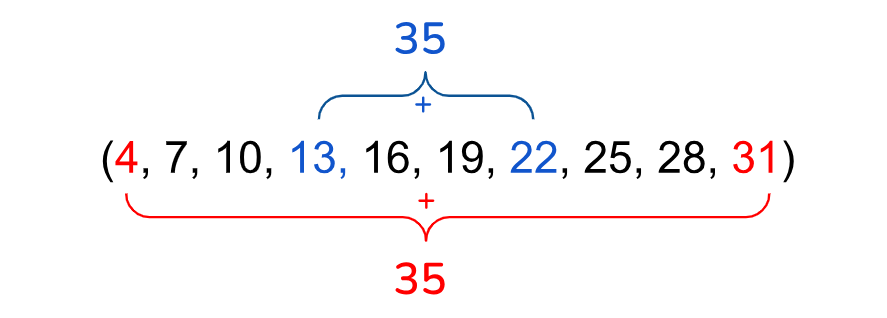
Dentro do universo de uma progressão aritmética finita, existe um padrão curioso: ao somar quaisquer dois termos que estão igualmente distantes das pontas, o resultado é sempre o mesmo que a soma dos termos extremos da sequência.

A imagem mostra a PA (4, 7, 10, 13, 16, 19, 22, 25, 28, 31). A soma dos valores 13 mais 22 é igual a 35. A soma dos termos mais extremos da sequência, 4 mais 31 também é igual a 35

Segunda propriedade

Quando temos uma progressão aritmética finita com uma quantidade ímpar de termos, algo fascinante acontece: o termo que fica exatamente no meio da sequência é igual à média aritmética dos termos que estão à mesma distância dele de ambos os lados. Esta intrigante característica flui naturalmente a partir da definição básica de uma PA.

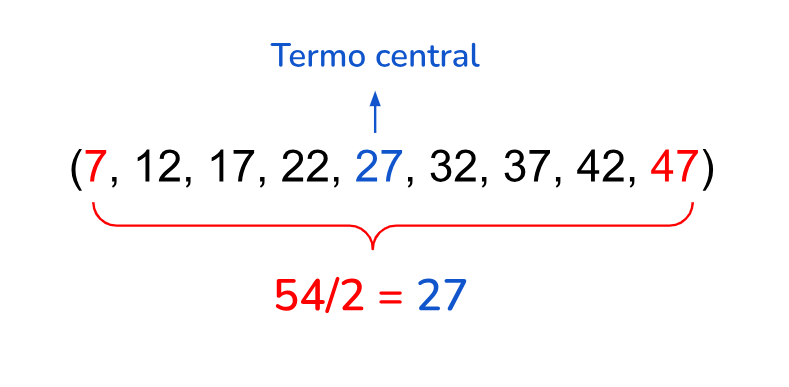
Dada a progressão aritmética finita (7, 12, 17, 22, 27, 32, 37, 42 e 47), o termo central é o 27. Somando os termos mais extremos 7 e 47 e fazendo a média aritmética temos 7 mais 47 igual a 54, dividido por 2 é igual a 27, o termo central

Dessa forma, como podemos visualizar na sequência acima, a soma dos extremos (7 + 47) é igual a 54. Ao fazer a média aritmética desta adição, resulta em 27, igual ao termo central da progressão aritmética.

Termo do meio da PA

Outra característica das progressões aritméticas é que, quando temos três termos consecutivos, podemos escrever o termo do meio como a média aritmética dos termos das pontas:

Considerando a sequência $(a_n,\;a_{n+1},\;a_{n+2})$, temos que:

$a_{n+1}=\dfrac{a_{n}+a_{n+2}}{2}$

Podemos utilizar tal relação para encontrar valores de termos de uma PA em questões em que só sabemos os valores dos termos nos extremos. Por exemplo, na PA $(5,\;x,\;11)$, utilizando a relação do termo médio, sabemos que o valor de $x$ é $(5+11)/2=8$.

Soma de termos de uma PA

Imagine a sequência de números $(1,\; 2,\; 3,\; 4,\; 5,\; ... ,\; 100)$. O que você faria para calcular a soma de todos os números desta sequência sem adicionar termo a termo? Este foi um problema apresentado ao matemático Karl Friedrich Gauss durante sua época na escola.

Retrato de Karl Friedrich Gauss (Imagem: Gauß-Gesellschaft Göttingen e.V./Wikimedia Commons)

Gauss notou que, ao somar os extremos desta sequência, sempre resultava no mesmo valor. Ele fez isto separando os valores em duas linhas da seguinte maneira:

1	2	...	49	50
100	99	...	52	51

Após isso, ele adicionou mais uma linha onde os valores representavam a soma dos termos que estavam na mesma coluna, ficando com:

	1	2	...	49	50
+	100	99	...	52	53
=	101	101	...	101	101

Assim, notando que o resultado da soma era sempre o mesmo, ele percebeu que a soma de todos os termos da sequência será a soma das 50 vezes que o número $101$ aparece. Dessa forma, $101\cdot 50$ resultando em $5050$.

Percebe-se que cada par de termo que foi somado na PA original se tornou um único valor. Neste caso, o $101$. Assim, conclui-se que a quantidade de vezes que o $101$ aparece é metade da quantidade de termos da PA original.

Então, pensando de forma genérica, podemos expressar a soma dos termos de uma PA qualquer com a seguinte expressão:

$S_n=\dfrac{(a_1+a_n)\cdot n}{2}$

Onde:

$S_n$: soma dos n termos.
$a_1$: primeiro termo.
$a_n$: $n$-ésimo termo.
$n$: posição do $n$-ésimo termo.

Exemplo - Fórmula da soma de termos de uma PA

Considere a P.A. $(17,\;19,\;21,\;…)$. Deseja-se descobrir o valor da soma dos 100 primeiros termos. Então, qual é este valor?

Resposta: [11.600]
Na P.A. $(17,\;19,\;21,\;...)$, temos que:

Primeiro termo: $a_1=17$
Razão: $r=2$
100º termo: $a_{100}=215$

Com tais informações, podemos utilizar a fórmula da soma dos termos de uma PA para encontrar o valor dos 100 primeiros termos da PA $(17,\;19,\;21,\;...)$. Aplicando a fórmula $S_n=\dfrac{(a_1+a_n)\cdot n}{2}$, temos que:

$S_n=\dfrac{(a_1+a_n)\cdot n}{2}$

$S_{100}=\dfrac{(17+215)\cdot 100}{2}$

$S_{100}=\dfrac{(232)\cdot 100}{2}$

$S_{100}=\dfrac{23200}{2}$

$S_n=11600$

Assim, a soma dos 100 primeiros termos da PA $(17,\;19,\;21,\;...)$ é 11600.

Resumo: progressão aritmética

Veja os principais pontos sobre o assunto:

Progressão aritmética (PA) é escrita como uma lista (1, 2, 3, 4, 5, 6, ...);
O símbolo $(...)$ significa que ela segue infinitamente. Logo, caracterizando-a como uma PA infinita;
Os termos são denotados por $a_n$ onde $n$ é o valor da sua posição;
Para encontrar a razão $r$ de uma PA, basta subtrair um termo qualquer do seu termo antecessor;
PAs constantes têm todos os termos iguais e razão igual a zero;
Nas PAs crescentes, os termos vão aumentando e sua razão é positiva;
Nas PAs decrescentes, os termos vão diminuindo e sua razão é negativa;
A fórmula do termo geral de uma PA é $a_n=a_1+(n+1)\cdot r$;
PAs finitas possuem a propriedade de que a soma dos termos dos extremos é igual a soma de dois termos que estão igualmente distantes das pontas;
PAs finitas com quantidade de termos ímpar têm a propriedade de que a soma dos termos dos extremos é igual ao termo central;
O termo central de três termos consecutivos é igual a média aritmética dos termos dos extremos;
A soma dos n primeiros termos de uma PA é igual a $S_n=\dfrac{(a_1+a_n)\cdot n}{2}$.

Como a PA cai no Enem e vestibulares

Nas questões do Enem, o conteúdo de progressão aritmética nunca é cobrado sozinho. Assim, muitas vezes, exige conhecimentos de geometria plana e espacial, além de uma boa interpretação para identificar os instrumentos da PA dentro do contexto do exercício.

Exemplo 1

(Enem 2018) A prefeitura de um pequeno município do interior decide colocar postes para iluminação ao longo de uma estrada retilínea, que inicia em uma praça central e termina numa fazenda na zona rural. Como a praça já possui iluminação, o primeiro poste será colocado a 80 metros da praça, o segundo, a 100 metros, o terceiro, a 120 metros, e assim sucessivamente, mantendo-se sempre uma distância de vinte metros entre os postes, até que o último poste seja colocado a uma distância de 1.380 metros da praça. Se a prefeitura pode pagar, no máximo, R$ 8.000,00 por poste colocado, o maior valor que poderá gastar com a colocação desses postes é

a) R$ 512.000,00.

b) R$ 520.000,00.

c) R$ 528.000,00.

d) R$ 552.000,00.

e) R$ 584.000,00.

Resposta: [C]
O objetivo é encontrar a quantidade de postes colocados para então assim descobrir o valor máximo pago pela prefeitura. Sabemos que o primeiro poste é colocado a uma distância de 80 metros do ponto inicial e após isto é colocado a cada 20 metros um novo poste, assim temos uma progressão aritmética com razão igual a 20 metros. Além disto sabemos que o primeiro termo está a 80 metros do ponto inicial, assim $a_1=80$, sabendo que o último poste está no final cujo o valor em metros do ponto inicial é 1380, assim sabemos que $a_n=1380$, utilizando a fórmula do termo geral da PA $a_n=a_1+(n+1)\cdot r$, substituindo os valores temos que:

$1380=80+(n-1)\cdot 20$
$1380=80+20n-20$
$1380=60+20n$
$1380-60=20n$
$1320=20n$

$n=\dfrac{1320}{20}$

$n=66$

Assim sabemos que serão colocados 66 postes, multiplicando por 8000 para saber o valor máximo temos que: $66\cdot 80000=528.000$

Exemplo 2

(Enem 2016) Sob a orientação de um mestre de obras, João e Pedro trabalharam na reforma de um edifício. João efetuou reparos na parte hidráulica nos andares 1, 3, 5, 7, e assim sucessivamente, de dois em dois andares. Pedro trabalhou na parte elétrica nos andares 1, 4, 7, 10, e assim sucessivamente, de três em três andares. Coincidentemente, terminaram seus trabalhos no último andar. Na conclusão da reforma, o mestre de obras informou, em seu relatório, o número de andares do edifício. Sabe-se que, ao longo da execução da obra, em exatamente 20 andares, foram realizados reparos nas partes hidráulica e elétrica por João e Pedro. Qual é o número de andares desse edifício?

a) 40

b) 60

c) 100

d) 115

e) 120

Resposta: [D]
Nesta questão, vamos considerar a sequência, os andares onde foram realizados reparos tanto por João e Pedro, assim sabemos que $a_1=1$, pois ambos fizeram reparos no primeiro andar, ao analisar a sequência dada pelo exercício podemos notar também que o próximo andar a receber reparos de ambos foi o andar 7, logo $a_2=7$. Subtraindo $7-1$ para encontrar a razão sabemos então que a razão da PA em questão é $6$. Como fomos informados que foram 20 andares que receberam ambos os reparos, temos então que descobrir o valor do $a_{20}$.
Utilizando a fórmula do termo geral da PA, temos que:

$a_{n}=a_1+(n-1)\cdot r$
$a_{20}=1+(20-1)\cdot 6$
$a_{20}=1+(19)\cdot 6$
$a_{20}=1+114$
$a_{20}=115$

Dessa forma, sabemos que o prédio possui 115 andares.

Exemplo 3

(Fuvest 2022) Uma empresa construiu um poço para armazenar água de reuso. O custo para construir o primeiro metro foi de R$ 1.000,00, e cada novo metro custou R$ 200,00 a mais do que o imediatamente anterior. Se o custo total da construção foi de R$ 48.600,00, a profundidade do poço é:

a) 15 m

b) 18 m

c) 21 m

d) 24 m

e) 27 m

Resposta: [D]
A frase presente no enunciado "custou R$ 200,00 a mais do que o imediatamente anterior" evidencia que é um problema de progressão aritmética porque temos somas iguais. Sabendo que o custo total foi R$ 48.600,00, temos a soma de todas as parcelas, onde n é o número de metros construídos, $S_n=48.600$. Como o preço pago pelo primeiro metro foi R$ 1.000,00 sabemos então que $a_1=1000$ e, de imediato, sabemos que a razão é 200.

Então, utilizando o termo geral, temos que: $a_n=1000+(n-1)\cdot 200=1000+200n-200=800+200n$

Assim, sabemos que $a_n =800+200n$

Utilizando a fórmula da soma dos n termos de uma PA, temos que:
$S_n=\dfrac{(a_1+a_n)\cdot n}{2}$

$48.600=\dfrac{(1000+800+200n)\cdot n}{2}$
$97200=1000n+800n+200n^2$
$200n^2+1800n-97200=0$

Dividindo tudo por 200, temos:

$n^2+9n+486=0$

Resolvendo a equação do segundo grau, temos que:
$n=(18,\;-27)$ porém, o valor negativo não convém, logo $n=18$

Dessa forma, a profundidade do poço é de 18 metros.

Quer estudar mais conteúdos de Matemática para o vestibular? Então conheça a plataforma do Aprova Total e conquiste a sua aprovação na universidade dos sonhos!