Probabilidade: conceitos, cálculo e exercícios resolvidos

Provavelmente, você já se perguntou quais as chance de ganhar na Mega-Sena. Ou até se, em meio a essa onda de calor que estamos vivendo, quais as chances de chover hoje. Podemos dizer que esses questionamentos são problemas de Matemática, especificamente do campo da probabilidade.

Ele busca estudar os experimentos aleatórios, ou seja, situações onde os resultados são incertos e variam a cada repetição. A teoria das probabilidades fornece um arcabouço sólido para lidar com essas incertezas e responder a tais perguntas de forma rigorosa. Ela nos ajuda a quantificar as chances e os riscos associados a diferentes eventos, o que permite tomar decisões fundamentadas.

O que é probabilidade?

A probabilidade é um conceito fundamental da Matemática que permeia inúmeras áreas do conhecimento, como a Economia, e também está em nosso cotidiano. Trata-se da medida da incerteza ou chance associada a um evento, que fornece ferramentas poderosas para tomar decisões nas situações em que o resultado é desconhecido ou imprevisível.

Por meio da análise probabilística, podemos modelar e compreender uma variedade de fenômenos complicados, desde previsões meteorológicas até avaliações de risco financeiro, algo essencial em um mundo onde a incerteza é a única constante.

Um exemplo de problema de probabilidade comum é o cálculo da probabilidade de obter um número específico de um dado não viciado de seis lados.

Conceitos importantes de probabilidade

Antes de partimos para problemas que envolvem probabilidade, precisamos estar atentos aos conceitos fundamentais que cercam este ramo.

Experimentos aleatórios

Um experimento aleatório é um processo ou evento cujo resultado não pode ser previsto com certeza antes de ser realizado. Em outras palavras, é uma situação de incerteza sobre qual resultado específico ocorrerá.

Como vimos, lançar um dado não viciado é um tipo de experimento aleatório. Antes de lançar o dado, você sabe que há seis possíveis resultados, representados pelos números de 1 a 6. No entanto, não conseguimos prever com certeza qual número específico vamos obter em um lançamento particular até que o dado seja jogado.

Outros exemplos de experimentos aleatórios incluem:

• lançar uma moeda justa para determinar se cai cara ou coroa;
• retirar uma carta de um baralho embaralhado para ver qual carta é escolhida;
• medir a temperatura de um paciente no hospital, uma vez que vários fatores podem influenciar a leitura.

Usamos a teoria das probabilidades para modelar e analisar experimentos aleatórios, o que permite calcular as chances de diferentes resultados ocorrerem e tomar decisões baseadas nessas probabilidades.

O contrário de experimento aleatório é o experimento determinístico. Sobre ele, nós sabemos qual será o resultado. Quer um exemplo? Sabemos que a água (sob pressão de 1 atm), ao aquecer até 100º C, entra em ebulição.

Espaço amostral

Espaço amostral é o conjunto de todos os casos possíveis em um experimento aleatório. Vejamos um exemplo para melhor entender este conceito.

Sabemos que um dado não viciado de seis lados, ao ser jogado possui 6 possibilidades de resultados, o resultado é o número da face voltada para cima.

Assim o espaço amostral deste experimento é representado como:

\(\left\{1,\;2,\;3,\;4,\;5,\;6 \right\}\)

O espaço amostral é uma parte fundamental na análise de probabilidade, pois ajuda a determinar as chances de cada resultado possível. Ao conhecer o espaço amostral e essa distribuição das probabilidades, é possível fazer previsões e decidir com base nos resultados de um experimento aleatório.

Espaços amostrais equiprováveis

O espaço amostral equiprovável é uma situação em que todos os resultados possíveis em um experimento aleatório têm a mesma probabilidade de ocorrência. Isso significa que, no experimento equiprovável, cada resultado individual tem a mesma chance de acontecer.

Vejo que o exemplo anterior é um espaço amostral equiprovável, pois independente do número desejado, ele tem sempre a mesma chance em relação aos outros.

Um exemplo com espaço amostral não equiprovável é a situação em que temos uma urna com 10 bolas de cor azul, 5 de cor vermelha e 2 de cor branca. Ao retirar um bola qualquer, sem olhar para a caixa, a chance de pegar uma bola azul é maior, pois há mais bolas dessa cor.

Eventos

Evento é a descrição de um subconjunto do espaço amostral. Em outras palavras, são casos específicos do espaço amostral.

Considere o experimento em que lançamos uma moeda duas vezes e desejamos obter, no primeiro lançamento, cara, e no segundo, coroa.

Primeiramente, construindo o espaço amostral deste experimento temos todos os possíveis casos:

\(\text{C}=\text{Cara}\)

\(\text{K}=\text{Coroa}\)

\(\text{Espaço Amostral}=\left\{\left(C,\;C\right),\;\left(C,\;K\right),\;\left(K,\;K\right),\;\left(K,\;C\right)\right\}\)

Agora, note que desejamos obter, no primeiro lançamento, cara, e no segundo, coroa - este caso em específico é o nosso evento:

\(\text{Evento}=\left\{\left(C,\;K\right)\right\}\)

O evento é um caso específico do espaço amostral, matematicamente falando, é um subconjunto do espaço amostral.

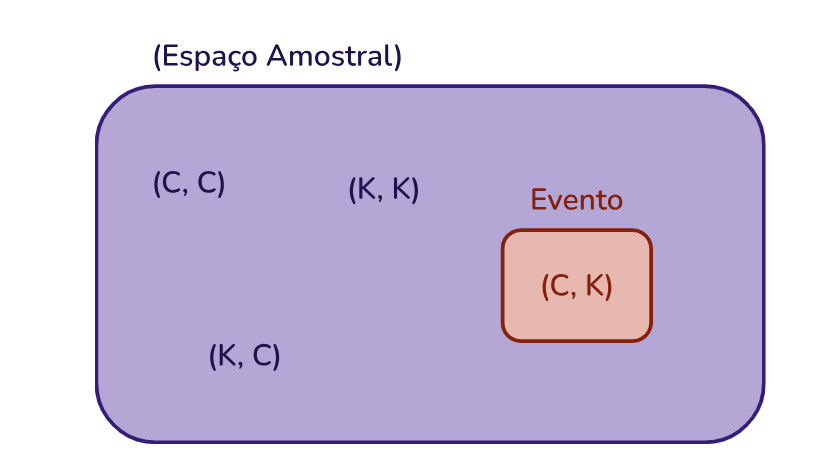
Agora podemos nos perguntar: qual é a chance de o evento acontecer? A resposta é 1/4, pois de todos os 4 casos possíveis, desejamos que apenas um deles aconteça.

Existem ainda situações em que os eventos têm nomes específicos, por possuírem certa característica em relação ao espaço amostral.

Evento certo: o evento é igual ao espaço amostral.

Exemplo: em um lançamento de dois dados de 6 lados, a soma de seus resultados ser maior que um.

Evento impossível: os eventos não contemplam nenhum caso do espaço amostral.

Exemplo: um dado de 6 lados, ao ser lançado, resultar em 7.

Evento complementar: os conjuntos de dois eventos formam todo o espaço amostral, além disso, a intersecção entre eles é vazia.

Exemplo: ao lançar um dado de 6 lados não viciado, os eventos são complementares se resultarem em um número par e em um número ímpar, pois a união dos dois contemplam todos os casos do espaço amostral.

Evento mutuamente exclusivo: a intersecção de dois eventos é vazia, ou seja, não podem ocorrer ao mesmo tempo.

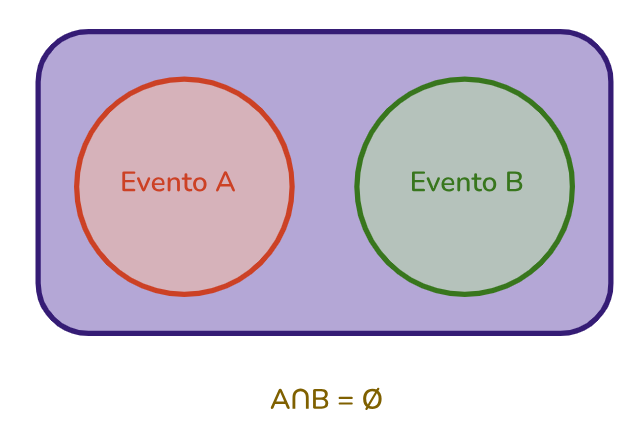
Exemplo: no lançamento de um dado de 6 lados, os resultados 5 e 6 são eventos mutuamente exclusivos, pois não podem ocorrer ao mesmo tempo

Cálculo de probabilidades

A fórmula para calcular uma probabilidade é relativamente simples e podemos encontrá-la ao dividir o número de eventos favoráveis e o número total de resultados possíveis.

Seja um evento \(A\) e um espaço amostral \(S\), a notação \(n(A)\) e \(n(S)\) se refere à quantidade de elementos nestes conjuntos, e P(A) se refere à probabilidade de o evento A acontecer dado pela fórmula:

\(\text{P(A)}=\dfrac{\text{n(A)}}{\text{n(S)}}=\dfrac{\text{Número de casos do evento}}{\text{Número de casos do espaço amostral}}\)

Os valores da probabilidade podem ser expressos em frações ou em porcentagens.

🚨 Não se esqueça de que o símbolo da porcentagem é "%" e ela é expressa em 1/100 🚨

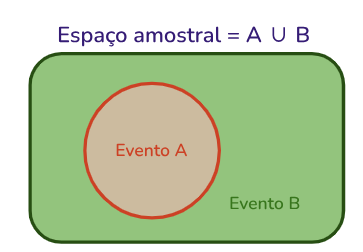
Probabilidade da união

Na probabilidade da união de dois eventos, denotada por \(P(A \cup B)\), queremos calcular a probabilidade de um evento A ou B ocorrer. Calculamos somando a probabilidade de A + a probabilidade do evento B, e precisamos subtrair deste cálculo os casos em que o evento A e o evento B acontecem ao mesmo tempo - o que é chamado da intersecção entre os dois eventos \(P(A\cap B)\).

Vejo no esquema a seguir:

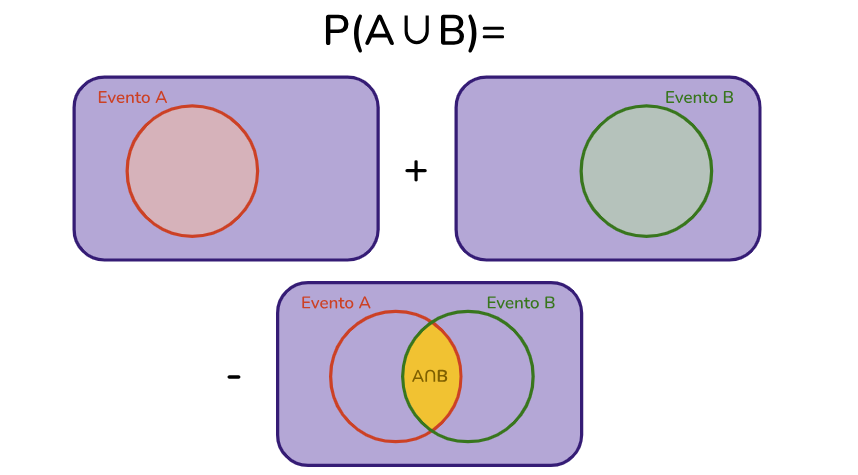
Perceba que a intersecção foi contabilizada duas vezes, por este motivo subtraímos ela uma vez.

Com base no diagrama acima temos que a fórmula para o cálculo da probabilidade da união de dois eventos é dada por:

\(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)

Para eventos que são mutuamente exclusivos, a intersecção é vazia, logo, podemos ignorá-la na fórmula:

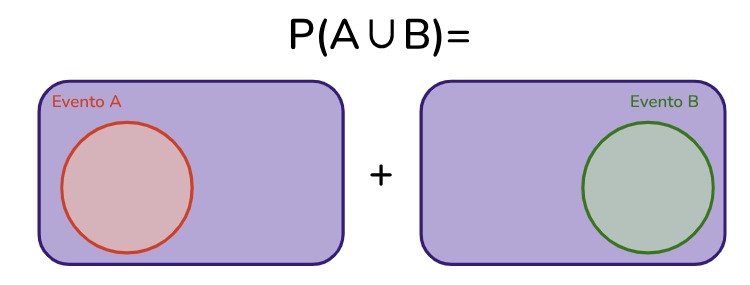
Neste caso, não contabilizamos a intersecção, pois ela é um conjunto vazio:

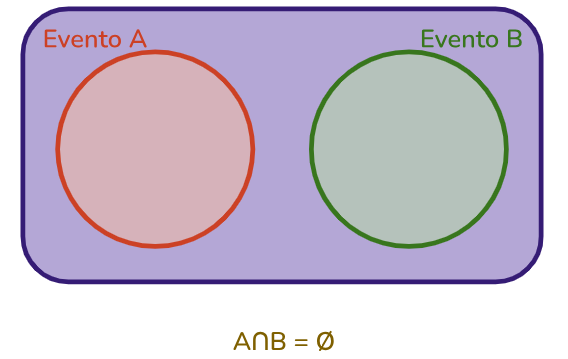
Assim a fórmula é dada por:

\(P(A\cup B)=P(A)+P(B)\)

Probabilidade complementar

Dois eventos são complementares quando a intersecção entre eles é vazia e a essa união contempla todos os casos do espaço amostral. Assim, seja A um evento complementar ao evento B, temos que:

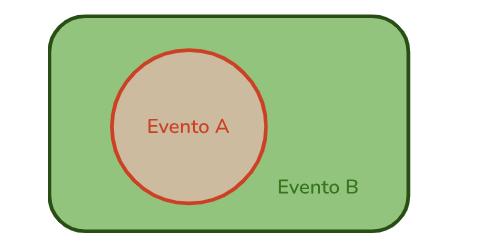
A notação para o complementar de um evento pode ser a letra do evento com uma barra encima:

\(\overline{A}\)

Além disto temos a seguinte relação:

\(P(\overline{A})=1-P(A)\)

Exemplo de eventos complementares

Considerando o experimento de lançar um dado de 6 lados não viciado e considerando o evento A ter como resultado um número menor ou igual a 3, temos que:

\(\text{Espaço amostral}=\left\{1,\;2,\;3,\;4,\;5,\;6\right\}\)

\(\text{Evento(A)}=\left\{1,\;2,\;3\right\}\)

\(\text{Evento}(\overline{A})=\left\{4,\;5,\;6\right\}\)

Perceba que o Evento A não possui nenhum caso igual ao seu complementar e a união de ambos resulta no espaço amostral caracterizando-os como eventos complementares.

Não se esqueça de que falar sobre "complementar" só faz sentido se o espaço amostral está bem estabelecido, pois, caso contrário, o complementar de um evento pode ser...

...o universo inteiro. 🤯

Probabilidade condicional

A probabilidade condicional é a probabilidade de um determinado evento ocorrer, sabendo que outro condicionante já aconteceu. Em dois eventos A e B, a probabilidade condicional é representada por \(P(A|B)\) e significa a probabilidade do evento A ocorrer, dado que o evento B ocorreu.

Podemos calcula-lo utilizando a seguinte fórmula:

\(P(A|B)=\dfrac{P(A\cap B)}{P(B)}\)

Vale ressaltar que os eventos A e B devem ter o mesmo espaço amostral.

Probabilidade da intersecção e eventos independentes

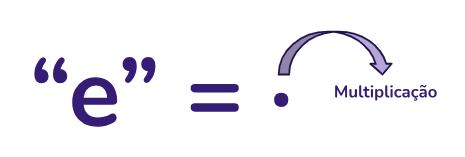
A probabilidade da intersecção, muitas vezes denotada como \(P(A \cap B)\), se refere à probabilidade de que de um evento A e um evento B aconteça. Em termos simples, é a chance de que ambos os eventos aconteçam ao mesmo tempo. A fórmula geral para calcular a probabilidade da intersecção é:

\(P(A\cap B)=P(B|A)\cdot P(A)=P(B)\cdot P(A|B)\)

Visualmente ele representa os casos comum entre os dois eventos:

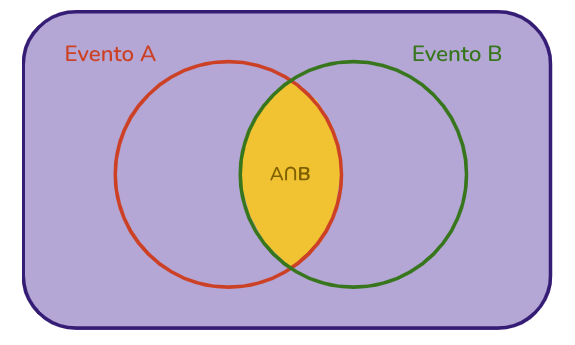
Se os eventos A e B forem independentes (ou seja, se a ocorrência de um não interferir na probabilidade de ocorrer outro), a fórmula para o cálculo da probabilidade da intersecção será dada por:

\(P(A\cap B)=P(A)\cdot P(B)\)

Exercícios resolvidos de probabilidade: Enem e vestibulares

Confira alguns exemplos de exercícios resolvidos sobre o tema:

Exemplo 1

(Espcex (Aman))  Numa sala existem duas caixas com bolas amarelas e verdes. Na caixa 1, há 3 bolas amarelas e 7 bolas verdes. Na caixa 2, há 5 bolas amarelas e 5 bolas verdes. De forma aleatória, uma bola é extraída da caixa 1, sem que se saiba a sua cor, e é colocada na caixa 2. Após esse procedimento, a probabilidade de extrair uma bola amarela da caixa 2 é igual a: 

a) 49/110
b) 51/110
c) 53/110
d) 57/110
e) 61/110

Resposta [C]
Temos dois casos a considerar:

i) retirada de uma bola amarela da caixa 1 e de outra amarela da caixa 2
Neste caso temos que a probabilidade de retirar uma bola amarela da primeira caixa é 3/10 e da segunda caixa é 6/11. Como neste caso estamos utilizando a conjunção "E" multiplicamos ambos os resultados:
3/10 · 6/11

ii) retirada de uma bola verde da caixa 1 e de uma amarela da caixa 2
Neste caso temos que a probabilidade de retirar uma bola verde da primeira caixa é 7/10 e retirar da segunda caixa uma bola amarela é 5/11. Como neste caso estamos utilizando a conjunção "E" multiplicamos ambos os resultados:
7/10 · 5/11

Desse modo, devemos somar ambos os resultados pois queremos um "OU" outro, a resposta é dada por: 3/10 · 6/11 + 7/10 · 5/11 = 53/110

Exemplo 2

(Enem PPL)  Para um docente estrangeiro trabalhar no Brasil, ele necessita validar o seu diploma junto ao Ministério da Educação. Num determinado ano, somente para estrangeiros que trabalharão em universidades dos estados de São Paulo e Rio de Janeiro, foram validados os diplomas de 402 docentes estrangeiros. Na tabela, está representada a distribuição desses docentes estrangeiros, por países de origem, para cada um dos dois estados.

	Argentina	Espanha	Cuba	Portugal	Venezuela	Total de docentes
São Paulo	112	60	28	9	30	239
Rio de Janeiro	29	40	46	36	12	163
Total	141	100	74	45	42	402

A probabilidade de se escolher, aleatoriamente, um docente espanhol, sabendo-se que ele trabalha em uma universidade do estado de São Paulo é

a) 60/402
b) 60/239
c) 60/100
d) 100/239
e) 279/402

Resposta [B]
Perceba que queremos saber a probabilidade de ser um espanhol sabendo que ele trabalha em uma universidade de São Paulo. Se A é o evento "docente espanhol" e B é o evento "trabalha em uma universidade do estado de São Paulo", então queremos calcular P(A|B).

Sabendo pela tabela, que o número de professores espanhóis que lecionam em São Paulo é: n(A ∩ B) = 60

Além disto sabemos o número de professores estrangeiros que trabalham em São Paulo é n(B)= 239.

Dado a fórmula de probabilidade condicional sabemos que:
P(A|B)=(n(A ∩ B))/(n(B))
=60/239

Exemplo 3

(UFPR) Um kit para impressão vem com oito cartuchos de tinta, de formato idêntico, para impressora. Nesse kit há dois cartuchos de cada uma das quatro cores diferentes necessárias para uma impressora caseira (ciano, magenta, amarelo e preto). Escolhendo aleatoriamente dois cartuchos desse kit, qual a probabilidade de se obter duas cores distintas?

a) 6/7
b) 1/12
c) 15/56
d) 1/48
e) 1/64

Resposta: [A]
Como são dois cartuchos de cada uma das quatro cores, não importa qual o cartucho pegar, a probabilidade de pegar outro cartucho da mesma cor é 1/7, pois há apenas mais um cartucho daquela cor dentre os 7 cartuchos que restaram. Desse modo, a probabilidade de pegar dois cartuchos de cores distintas é o complementar, ou seja 1 - 1/7 = 6/7