Cinemática: conceitos fundamentais, fórmulas e como cai no Enem
A cinemática é uma das áreas da Física que mais aparece no Enem. A partir dela, estudamos os movimentos das coisas! Confira quais exercícios podem ser cobrados nas provas

Acessibilidade
Nas provas de Física, a cinemática quase sempre dá as caras em posição de destaque, seja nos vestibulares em geral ou no Exame Nacional do Ensino Médio (Enem), em que esse é 4º assunto de maior incidência, representando 11,5% das questões.
A seguir, explicamos os conceitos básicos de cinemática e suas principais fórmulas, e você ainda lê um resumo de como o Enem cobra esse conteúdo.
NAVEGUE PELOS CONTEÚDOS
Introdução à cinemática: o que essa área da Física estuda?
A cinemática faz parte da mecânica, uma das grandes áreas da Física e a mais antiga. Ela estuda as situações de movimento e de repouso dos corpos. Então, com os conhecimentos de mecânica, podemos usar grandezas como velocidade, força e energia para estudar esses cenários.
No caso da cinemática, o objetivo é descrever o movimento dos corpos, mas sem se preocupar com suas causas. Em outras palavras, a cinemática nos permite conhecer a velocidade de um corpo, saber onde ele vai estar daqui a algum tempo, se ele tem aceleração, como é a trajetória de seu movimento e mais.
Com a frase "sem se preocupar com suas causas", queremos dizer que a cinemática apenas descreve o movimento, mas sem buscar suas origens e efeitos. Ou seja, não introduzimos conceitos como força e energia, pois isso fica a cargo de outras partes da mecânica.
Conceitos fundamentais de cinemática
Para começar bem os estudos de cinemática, precisamos aprender alguns de seus conceitos e fundamentos básicos. Isso é importante não somente para entender assuntos posteriores da área, mas para afiar a resolução de questões, já que o Enem e outros vestibulares cobram muitos desses conhecimentos básicos.
Referencial
Não apenas na cinemática, mas na Física como um todo, a ideia de referencial é muito importante: é a partir dele que analisamos a situação estudada e fazemos medidas daquilo que está acontecendo.
Um referencial é o sistema a partir do qual tomamos medidas, como posição, deslocamento e velocidade (que conheceremos nos próximos parágrafos), e utilizamos para analisar se um corpo está em movimento ou em repouso.
Espaço (posição)
O espaço (ou posição) de um corpo nos diz onde ele se encontra em um certo referencial. Isso já demonstra a importância de adotar um referencial, pois, ao determiná-lo e considerar marcações de posição (que podem ser imaginárias), podemos localizar qualquer outro corpo nesse referencial.
As marcações de quilômetros presentes na rodovia são um bom exemplo.

Medimos posições usando unidades de comprimento/distância, como o metro (que é a unidade no Sistema Internacional), o quilômetro e a milha.
Repouso e movimento
Você sabia que, do ponto de vista da Física, um corpo pode estar em repouso e em movimento ao mesmo tempo? Isso porque repouso e movimento dependem de um referencial.
Para certo referencial, um corpo está em repouso se sua posição não variar. Caso sua posição varie, dizemos que o corpo está em movimento. Assim, dependendo do referencial que usarmos, o corpo pode estar em movimento, mas em repouso em relação a outro referencial.
Se considerarmos, por exemplo, o motorista dentro do carro na foto abaixo, podemos dizer que ele está em repouso em relação ao referencial do carro, pois em relação ao carro, sua posição não varia (ele está parado).

Contudo, no referencial da estrada, o motorista está em movimento, pois ele está se movendo junto com o carro, que está em movimento em relação à estrada.
Trajetória
A trajetória de um corpo em movimento corresponde ao conjunto de todas as posições que ele ocupou ao longo desse movimento. É uma linha que indica seu “rastro”, por onde ele passou.
O rastro de fumaça deixado no céu por um avião indica a sua trajetória. Nem todo movimento deixa uma trajetória explícita como nesse caso. Às vezes, usamos uma linha imaginária para representar a trajetória de um corpo.
A ideia de referencial também é muito importante quando falamos de trajetória: um mesmo movimento pode ter trajetórias diferentes para dois referenciais distintos.

Por exemplo, no referencial do piloto, como ele está se movendo junto com o avião, a trajetória da hélice será circular. Entretanto, para o referencial de um observador parado no chão, a trajetória será diferente: além da hélice girar, o avião se desloca horizontalmente. A trajetória do ponto de vista do observador terá a seguinte forma:
Esse formato de “mola” é chamado de helicoidal. Ele é o resultado do movimento circular da hélice e de seu deslocamento horizontal.
Movimento progressivo e movimento retrógrado
Logo depois de determinar o referencial, podemos definir um sentido para ele. Veja no exemplo:
O carro está se movendo da esquerda para a direita ao longo de uma trajetória orientada com marcações de posição. A posição 0 m é a origem do referencial e é a partir dela que determinamos os outros valores de posição.
A partir da origem, o sentido que escolhemos para o referencial pode ser positivo ou negativo. Na imagem, todas as posições à direita da origem são positivas, então o sentido da esquerda para a direita é o sentido positivo (crescente) do referencial.
Da mesma forma, todas as posições à esquerda da origem são negativas, então o sentido da direita para a esquerda é o sentido negativo (decrescente) do referencial.
Quando um corpo se move no sentido positivo do referencial, dizemos que o movimento é um movimento progressivo. Se o corpo se mover no sentido negativo, o movimento é um movimento retrógrado ou regressivo. Esse tipo de classificação só depende de como escolhemos orientar o referencial.
Deslocamento escalar
Observe de novo a imagem do carro se movendo ao longo da trajetória orientada.
Veja que ele saiu da posição inicial s0 = -20 m e foi até a posição s = 30 m. As letras “s” são usadas para representar posição/espaço.
A esse movimento, podemos associar um deslocamento escalar (Δs), que corresponde à diferença entre as posições:
\[ \Delta s - s - s_0 \]
Assim, para o exemplo da imagem, o deslocamento escalar é Δs = 30 - (-20) = 30 + 20 = 50 m.
O deslocamento escalar também é chamado de variação da posição. No caso desse movimento, que já vimos ser um movimento progressivo, o deslocamento escalar tem sinal positivo. Caso o móvel realizasse um movimento retrógrado, o sinal do deslocamento escalar seria negativo, já que a posição s seria menor do que a posição s0.
É importante entender que deslocamento é uma grandeza vetorial, ou seja, possui módulo (valor), direção e sentido, podendo ser representado por um vetor. Entretanto, na cinemática em uma dimensão, é comum nos preocuparmos somente com o módulo e com o sentido.
Instante e intervalo de tempo
Definir tempo é uma tarefa extremamente complicada, pois tempo é considerado um conceito primitivo. Tentar dar uma definição precisa para tempo geralmente leva a raciocínios circulares, quando você usa um conceito para explicar o que é o próprio conceito.
O que entendemos sobre tempo é que é uma grandeza física escalar e que é uma forma de reconhecermos uma sequência correta de eventos a partir da ordem em que eles ocorrem.
A partir disso, a cinemática utiliza dois termos principais para falar de tempo: o instante e o intervalo de tempo.
Imagine o seguinte: voltando à mesma situação do carro, começamos a estudar seu movimento a partir da posição inicial s0 = -20 m. Quando o carro está passando por essa posição, é o momento em que ligamos um cronômetro para começar a contabilizar o tempo. Quando o carro passa pela posição s = 30 m, nós desligamos o cronômetro.
A ideia de instante (t) de tempo se refere a um tempo específico. Por exemplo: se o carro passou pela posição s = 0 m quando o cronômetro marcava 2 s, isso nos indica o instante em que o carro estava naquela posição.
Já a ideia de intervalo de tempo (Δt) remete a um conjunto de instantes. Podemos pensar no instante de t = 0 s até t = 2 s como um intervalo de tempo entre esses instantes.

Velocidade escalar média
A velocidade escalar média é uma grandeza que indica o quão rapidamente a posição de um móvel varia. Ela é dada pela razão entre o deslocamento escalar (Δs) e o intervalo de tempo (Δt) correspondente:
\[ v_M = \frac{\Delta s}{\Delta t} \]
Por ser a razão entre deslocamento e tempo, a unidade de velocidade escalar média será a razão entre uma unidade de deslocamento/distância e uma unidade de tempo. No Sistema Internacional, essa unidade é o metro por segundo (m/s). Também é comum trabalhar com quilômetro por hora (km/h).
No exemplo que vimos do carro, para ir da posição s0 = -20 m até a origem (s = 0 m), ou seja, para um deslocamento escalar de Δs = 20 m, o carro levou um intervalo de tempo de Δt = 2 s.
Podemos calcular a velocidade escalar média do carro a partir dessa definição:
\[ v_M = \frac{\Delta s}{\Delta t} \\
v_M = \frac{20}{2} \\
v_M = 10\ m/s
\]
Assim como aprendemos sobre o deslocamento escalar, podemos fazer uma consideração sobre a velocidade escalar média: velocidade é sempre uma grandeza vetorial, e não escalar.
No entanto, trabalhar com cinemática em uma dimensão possibilita tratar do conceito de velocidade média, em que não nos preocupamos com o caráter vetorial da velocidade.
As classificações em movimento progressivo e em movimento retrógrado também podem ser percebidas a partir da velocidade: se a velocidade é positiva, o móvel está indo no sentido positivo (movimento progressivo). Se é negativa, o móvel está indo no sentido negativo (movimento retrógrado).
⚠️ Alguns livros, vestibulares e professores definem velocidade escalar média como a razão entre a distância total percorrida (e não o deslocamento escalar) e o intervalo de tempo. Nesses casos, é importante entender como seu professor ou o vestibular que você quer fazer cobra esse conceito.
Velocidade escalar instantânea
A velocidade escalar média nos dá uma ideia da velocidade no percurso como um todo, mas não nos garante qual era o valor da velocidade do móvel em um instante específico. Para isso, consideramos a velocidade escalar instantânea, que indica a velocidade escalar em um dado instante.
Para calcular uma velocidade escalar instantânea, podemos pensar na razão Δs/Δt. Quanto menor for o intervalo Δt, mais próxima essa razão fica de um valor instantâneo da velocidade.
No Ensino Superior, usamos uma ferramenta matemática chamada limite, que permite calcular o valor exato de uma velocidade instantânea.
O velocímetro de um carro, por exemplo, marca valores de velocidades instantâneas do veículo.
Ponto material versus corpo extenso
Dizemos que um corpo é um ponto material quando suas dimensões não são relevantes na situação que estamos estudando. Quando calculamos a velocidade com que um carro viaja em uma rodovia, suas dimensões não importam, então podemos estudá-lo como se ele fosse um ponto.
Imagine que o mesmo carro vai ultrapassar um caminhão ou estacionar em uma vaga. Na situação de ultrapassagem, tanto o tamanho do caminhão quanto o do carro são importantes para calcularmos, por exemplo, o tempo de ultrapassagem. No caso do estacionamento, as dimensões do carro são relevantes para que ele ocupe corretamente a vaga.
Quando as dimensões do corpo são relevantes na situação que estudamos, dizemos que ele é um corpo extenso. Aqui, então, não podemos desprezar essas dimensões. Repare, a partir dos exemplos, que um mesmo corpo pode se comportar tanto como ponto material quanto como corpo extenso, dependendo da situação.
👉 Leia também:
Física no Enem: quais assuntos devem cair em 2023?
Ciências da Natureza: conheça 10 estratégias de estudo
Cinemática no Enem: como o assunto é cobrado?
Veja como o Enem aborda questões de cinemática, o 4º assunto de maior incidência nos últimos anos:
1. Movimento uniforme e velocidade média
O movimento uniforme (MU) ocorre com a velocidade escalar constante, ou seja, o móvel não fica mais rápido nem mais devagar ao longo do tempo: ele percorre espaços iguais em intervalos de tempo iguais. No Enem, muitas questões utilizam somente a definição de velocidade escalar média (vM = Δs/Δt).
Além disso, é importante saber trabalhar com unidades de velocidade, principalmente m/s e km/h. Lembre-se de que, para converter km/h em m/s, basta dividir o valor por 3,6 e, para fazer a conversão inversa, basta multiplicar por 3,6:
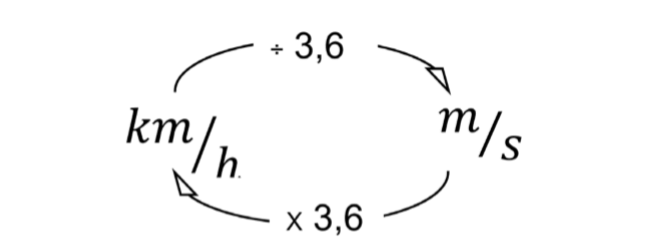
Exemplo
(Enem PPL 2013) Antes das lombadas eletrônicas, eram pintadas faixas nas ruas para controle da velocidade dos automóveis. A velocidade era estimada com o uso de binóculos e cronômetros. O policial utilizava a relação entre a distância percorrida e o tempo gasto, para determinar a velocidade de um veículo. Cronometrava-se o tempo que um veículo levava para percorrer a distância entre duas faixas fixas, cuja distância era conhecida. A lombada eletrônica é um sistema muito preciso, porque a tecnologia elimina erros do operador. A distância entre os sensores é de 2 metros, e o tempo é medido por um circuito eletrônico.
O tempo mínimo, em segundos, que o motorista deve gastar para passar pela lombada eletrônica, cujo limite é de 40 km/h, sem receber uma multa, é de:
a) 0,05
b) 11,1
c) 0,18
d) 22,2
e) 0,50
Resposta: [C]
Considerando a velocidade limite de 40 km/h, vamos usar a definição de velocidade média para calcular o tempo mínimo:
\[ v_M = \frac{\Delta s}{\Delta t} \\
\Delta t = \frac{\Delta s}{v_M}
\]
A distância Δs vale 2 m e a velocidade vM vale 40 km/h, mas precisamos converter para m/s para obter o tempo em s. Logo, devemos dividir por 3,6.
A razão 40/3,6 não fornece um resultado exato, então é útil manter na forma de fração, pois é possível simplificar ao longo do cálculo:
\[ \Delta t = \frac{2}{40/3,6} \\
\Delta t = \frac{2 \cdot 3,6}{40} \\
\Delta t = \frac{7,2}{40} \\
\Delta t = 0,18\ s
\]
Esse é um resultado exato, ou seja, não foi uma aproximação/arredondamento. Às vezes, manter na forma de fração uma divisão não-exata é uma boa escolha, como foi o caso desse exercício!
2. Movimento uniformemente variado
No movimento uniformemente variado (MUV) a velocidade escalar não é constante, ela varia de forma uniforme, ou seja, existe uma aceleração constante.
Os exercícios que cobram esse tipo de movimento no Enem geralmente estão contextualizados em acelerações de carros e trens, seja envolvendo aumento ou redução na velocidade escalar.
Dessa forma, é necessário encontrar uma das seguintes grandezas: velocidade (v), velocidade inicial (v0) aceleração (a), deslocamento (Δs) ou instante (t).
Existem três fórmulas que relacionam essas grandezas. Sendo assim, em cada exercício, utilize aquela que contém a grandeza que você procura e as que já estão presentes no enunciado da questão.
- \( s = s_0 + v_0 \cdot t + \frac{a \cdot t^2}{2} \) (Função horária da posição)
- \( v = v_0 + a \cdot t \) (Função horária da velocidade)
- \( v^2 = v_0^2 + 2 \cdot a \cdot \Delta s \) (Equação de Torricelli)
Exemplo
(Enem PPL 2020) Os acidentes de trânsito são causados geralmente por excesso de velocidade. Em zonas urbanas no Brasil, o limite de velocidade normalmente adotado é de 60 km/h. Uma alternativa para diminuir o número de acidentes seria reduzir esse limite de velocidade. Considere uma pista seca em bom estado, onde um carro é capaz de frear com uma desaceleração constante de 5 m/s2 e que o limite de velocidade reduza de 60 km/h para 50 km/h.
Nessas condições, a distância necessária para a frenagem desde a velocidade limite até a parada completa do veículo será reduzida em um valor mais próximo de
a) 1 m.
b) 9 m.
c) 15 m.
d) 19 m.
e) 38 m.
Resposta: [B]
Vamos identificar com (1) a situação antes da redução de velocidade e com (2) a situação após a redução de velocidade. Dessa forma, temos as seguintes informações:
v0(1) = 60 km/h = 17 m/s
v0(2) = 50 km/h = 14 m/s
a = - 5 m/s²
v = 0 m/s
É importante notar que o sinal negativo na aceleração indica que seu sinal é contrário ao da velocidade. Além disso, a velocidade v é nula porque, de acordo com o enunciado, o veículo para por completo.
Como queremos calcular distâncias e não temos informação do tempo, é interessante usar a equação de Torricelli. Vamos calcular, inicialmente, a distância de frenagem para a situação (1):
\[ v_{(1)}^2 = v_{0(1)}^2 + 2 \cdot a \cdot \Delta s_{(1)} \\
0^2 = 17^2 + 2 \cdot (-5) \cdot \Delta s_{(1)} \\
0 = 289 - 10 \cdot \Delta s_{(1)} \\
10 \cdot \Delta s_{(1)} = 289 \\
\Delta s_{(1)} = \frac{289}{10} \\
\Delta s_{(1)} = 28,9\ m \]
Fazendo a mesma coisa para a situação (2):
\[ v_{(2)}^2 = v_{0(2)}^2 + 2 \cdot a \cdot \Delta s_{(2)} \\
0^2 = 14^2 + 2 \cdot (-5) \cdot \Delta s_{(2)} \\
0 = 196 - 10 \cdot \Delta s_{(2)} \\
10 \cdot \Delta s_{(2)} = 196 \\
\Delta s_{(2)} = \frac{196}{10} \\
\Delta s_{(2)} = 19,6\ m \]
Por fim, como a questão quer a redução da velocidade, devemos tomar a diferença entre os valores encontrados:
\[ \Delta s = 28,9 - 19,6 \\
\Delta s = 9,3\ m \]
3. Queda livre e lançamento vertical
Calma lá, queda livre e lançamento vertical não são tipos de movimento uniformemente variado? Sim, você está certo! Porém, costumamos separar o estudo desses movimentos, pois diversos exercícios do Enem podem ser resolvidos usando apenas conceitos de gravidade, sem a necessidade do uso daquelas fórmulas que acabamos de ver.
Logo, nesses exercícios, tenha em mente que todo corpo em queda está sujeito a uma mesma aceleração, a aceleração da gravidade (g = 9,8 m/s², valor normalmente arredondado para 10).
Sendo assim, quando são soltos de uma mesma altura, desconsiderando a resistência do ar, todos os corpos, independentemente de suas massas, demoram a mesma quantidade de tempo para atingir o chão.
Exemplo
(Enem 2023) Um professor lança uma esfera verticalmente para cima, a qual retorna, depois de alguns segundos, ao ponto de lançamento. Em seguida, lista em um quadro todas as possibilidades para as grandezas cinemáticas.(Enem 2023) Um professor lança uma esfera verticalmente para cima, a qual retorna, depois de alguns segundos, ao ponto de lançamento. Em seguida, lista em um quadro todas as possibilidades para as grandezas cinemáticas.
*Grandezas com módulo nulo não têm sentido definido.
Ele solicita aos alunos que analisem as grandezas cinemáticas no instante em que a esfera atinge a altura máxima, escolhendo uma combinação para os módulos e sentidos da velocidade e da aceleração.
A escolha que corresponde à combinação correta é:
a) v = 0 e a ≠ 0 para cima.
b) v ≠ 0 para cima e a = 0.
c) v = 0 e a ≠ 0 para baixo.
d) v ≠ 0 para cima e a ≠ 0 para cima.
e) v ≠ 0 para baixo e a ≠ 0 para baixo.
Resposta: [C]
No ponto de altura máxima de um lançamento vertical, a velocidade é nula, pois é nesse ponto que há inversão no sentido do movimento. A aceleração, no entanto, é constante ao longo de todo o movimento, pois corresponde à aceleração gravitacional, que tem sempre direção vertical e sentido de cima para baixo.
4. Movimento circular uniforme
O movimento circular uniforme (MCU) é um movimento uniforme em que a trajetória é circular e a velocidade escalar do corpo é constante. Juntamente com movimento uniforme em geral, é o tema de cinemática que mais deu as caras no Enem nos últimos anos.
Nesse assunto, é importante focar nas grandezas velocidade linear (v), velocidade angular (ω) e raio de trajetória (R), e na relação entre elas:
\[ v = \omega\cdot R \]
Dessa forma, lembre-se de que a velocidade angular (ω) é medida em rotações por segundo (hertz) ou rotações por minuto (RPM), ou seja, ela mede quantos ciclos completos o corpo realiza por segundo.
A velocidade linear também pode ser representada a partir do raio (R) e da frequência (f).
\[ v = 2 \cdot \pi \cdot R \cdot f \]
Exercícios de MCU frequentemente são contextualizados em associações de polias ou de engrenagens, conforme a imagem:
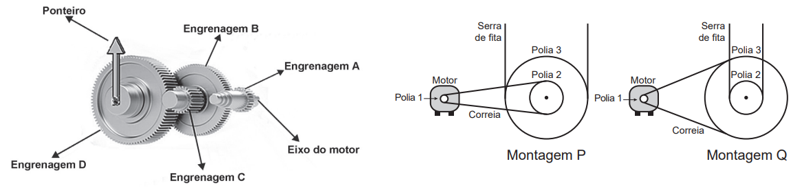
Lembre-se de que nesse tipo de exercício existem dois tipos de acoplamento: coaxial e tangencial:
- no acoplamento coaxial, as frequências, velocidades angulares e períodos são iguais;
- no acoplamento tangencial, as velocidades lineares são iguais.
Exemplo
(Enem 2016) A invenção e o acoplamento entre engrenagens revolucionaram a ciência na época e propiciaram a invenção de várias tecnologias, como os relógios. Ao construir um pequeno cronômetro, um relojoeiro usa o sistema de engrenagens mostrado. De acordo com a figura, um motor é ligado ao eixo e movimenta as engrenagens fazendo o ponteiro girar. A frequência do motor é de 18 rpm, e o número de dentes das engrenagens está apresentado no quadro.
A frequência de giro do ponteiro, em rpm, é
a) 1
b) 2
c) 4
d) 81
e) 162
Resposta: [B]
A Engrenagem B está acoplada tangencialmente à Engrenagem A, então suas velocidades lineares são iguais:
vB = vA
2πRBfB = 2πRAfA
Simplificando o “2π” dos dois lados: RBfB = RAfA, ou seja, a frequência de cada engrenagem é inversamente proporcional ao seu raio - quanto maior for o raio, menor será a frequência.
Além disso, o raio é proporcional ao número de dentes de cada engrenagem, que é a informação que temos, de modo que podemos escrever:
nBfB = nAfA
72 · fB = 24 · 18
fB = 432/72
fB = 6 RPM
A Engrenagem C e a Engrenagem B estão acopladas coaxialmente, logo, têm mesma frequência: fC = fB = 6 RPM. A Engrenagem D está acoplada tangencialmente à Engrenagem C, logo:
nDfD = nCfC
108 · fD = 36 · 6
fD = 218/108
fD = 2 RPM
Por fim, o ponteiro está acoplado coaxialmente à Engrenagem D, então sua frequência vale 2 RPM.
Resumo: cinemática
Confira abaixo um resumo dos tópicos mais importantes que aprendemos até aqui:
- Referencial: sistema a partir do qual tomamos medidas.
- Espaço (posição): representação de onde um corpo se encontra em um referencial.
- Repouso: estado em que a posição de um corpo não varia em um referencial.
- Movimento: estado em que a posição de um corpo varia em um referencial.
- Trajetória: conjunto de todas as posições que um móvel ocupa em um movimento.
- Movimento progressivo: ocorre no sentido positivo do referencial.
- Movimento retrógrado: ocorre no sentido negativo do referencial.
- Deslocamento escalar: diferença entre a posição final e a posição inicial de um movimento.
- Instante de tempo: refere-se a um tempo específico.
- Intervalo de tempo: refere-se a um conjunto de instantes.
- Velocidade escalar média: razão entre o deslocamento escalar e o intervalo de tempo.
- Velocidade escalar instantânea: valor exato da velocidade escalar em um dado instante.
- Ponto material: corpo cujas dimensões são irrelevantes para um determinado problema.
- Corpo extenso: corpo cujas dimensões importam para um determinado problema.
- Movimento uniforme: a velocidade escalar é constante.
- Conversão entre m/s e km/h: de km/h para m/s, dividimos por 3,6. De m/s para km/h, multiplicamos por 3,6.
- Movimento uniformemente variado: a velocidade escalar varia de forma uniforme, ou seja, a aceleração é constante.
- Queda livre: tipo de movimento uniformemente variado que ocorre na vertical e a aceleração é a gravidade.
- Movimento circular uniforme: movimento uniforme cuja trajetória é uma circunferência.




