Lançamento horizontal: tudo o que você precisa saber

Um lançamento horizontal consiste em arremessar horizontalmente um objeto, que passa a cair em trajetória parabólica. O "segredo" é que esse tipo de lançamento pode ser analisado como a composição de dois movimentos mais simples: um movimento uniforme e um movimento uniformemente variado.

Nesse post, você vai aprender o que é um lançamento horizontal, como podemos analisá-lo, quais são as suas equações e verá de que forma ele costuma aparecer nos vestibulares.

Como ocorre um lançamento horizontal?

Imagine que você dá um empurrão, na direção horizontal, em um objeto que está em cima de uma mesa. Uma bola, por exemplo. E se a bola alcançar a borda da mesa? Bom, sabemos que ela não vai seguir em linha reta, pois não há mais mesa abaixo dela. Ela também não cai para baixo como se tivesse sido solta de cima para baixo. Que tipo de movimento, então, essa bola realiza?

Para responder a isso, vamos precisar recorrer ao princípio da simultaneidade de Galileu. Esse princípio nos diz que o movimento de um corpo pode ser o resultado da composição de outros movimentos, que ocorrem simultaneamente.

Tá, mas como assim?

Vamos supor que podemos desprezar a resistência do ar e o atrito com a mesa. Assim, enquanto a bola se move sobre a mesa, as únicas forças que atuam sobre ela são o seu peso e a força normal que a mesa exerce. Quando a bola sai da mesa, essa força normal deixará de existir e apenas a força peso estará atuando.

É aí que entra a lógica de um lançamento horizontal: o peso da bola "puxa" ela para baixo, fazendo-a cair. Só que a bola já tinha uma velocidade na horizontal e não há motivo para que ela deixe de se mover horizontalmente. Como estamos desprezando a resistência do ar, não há uma força atuando sobre a bola nessa direção. Por inércia, ela permanecerá com essa velocidade.

No entanto, a força peso da bola continua atuando sobre ela. Dessa forma, ela também irá cair. Ao mesmo tempo em que ela continua indo "para a frente", ela está indo "para baixo".

Um lançamento horizontal nada mais é do que a superposição de dois movimentos que acontecem ao mesmo tempo: um movimento na horizontal e um movimento na vertical.

Movimento uniforme e movimento uniformemente variado

Vamos precisar lembrar um detalhe de vetores: podemos representar um vetor como sendo a soma de suas componentes na vertical e na horizontal. A velocidade é uma grandeza vetorial, então podemos usar essa lógica para a velocidade da bola.

Em cada instante do movimento, a velocidade da bola corresponde à soma vetorial da velocidade na horizontal com a velocidade na vertical.

Como vimos, na horizontal, não existem forças atuando sobre a bola. Assim, sua velocidade horizontal será constante, não aumentando e nem diminuindo, ao longo de todo o movimento. Em outras palavras: na horizontal, a bola descreve um movimento uniforme.

Já na vertical, sabemos que existe a força peso atuando, e ela é a força resultante sobre a bola. De acordo com a segunda lei de Newton, havendo uma força resultante atuando, há também uma aceleração envolvida. Nesse caso, a aceleração é a aceleração gravitacional (g). Dessa forma, na vertical, a bola cai de maneira acelerada, ou seja, na vertical, a bola descreve um movimento uniformemente variado (mais especificamente, uma queda livre).

Um movimento complexo como o de um lançamento horizontal pode ser simplificado se pensarmos nele como o resultado de dois movimentos mais simples que acontecem simultaneamente.

A trajetória de um lançamento horizontal

Se olhássemos essa bola sendo lançada horizontalmente, veríamos uma trajetória parabólica. Para um observador externo, em repouso, a trajetória de um lançamento oblíquo é um arco de parábola.

No entanto, a trajetória de um objeto depende do referencial. Nem sempre a trajetória de um objeto em lançamento horizontal vai ser uma parábola. Isso vai depender do referencial que está analisando.

Um exemplo clássico de lançamento horizontal nas questões de física é a situação onde um avião lança na horizontal um pacote com suprimentos. Se uma pessoa estivesse no solo, observando o avião no céu, quando o avião lançasse o pacote, essa pessoa perceberia uma trajetória parabólica do pacote.

Mas isso significa que qualquer pessoa veria essa trajetória? Não! Imagine um dos tripulantes do avião lançando o pacote. Ele apenas segura o pacote e, no momento adequado, o solta. Nesse caso, tanto o pacote quanto o avião têm a mesma velocidade horizontal. A diferença é que, ao ser solto, além de continuar indo para a frente, o pacote também irá cair.

Uma pessoa no solo, como vimos, veria uma trajetória parabólica. Mas o tripulante que o soltou, ao observar o movimento, veria apenas o pacote indo para baixo. Ele não perceberia que o pacote está se movendo horizontalmente, pois tanto ele quanto o pacote estão se movendo com a mesma velocidade horizontal!

Veja que, à medida em que o avião avança, o pacote avança a mesma distância horizontalmente. Além de avançar na horizontal, o pacote cai na vertical, proporcionando uma trajetória parabólica para um observador parado no chão e uma queda em linha reta para um observador no avião.

Equações de um lançamento horizontal

Vimos que um lançamento horizontal consiste em dois movimentos simultâneos: um movimento uniforme e um movimento uniformemente variado. A grande vantagem disso é que podemos analisar, individualmente, as equações para cada um desses movimentos.

Ao invés de fazer cálculos com a velocidade da bola, podemos fazer cálculos separados para cada um dos movimentos. Isso significa que vamos trabalhar com as componentes em x e em y da velocidade, e não com a velocidade em si. Bem melhor assim, né?

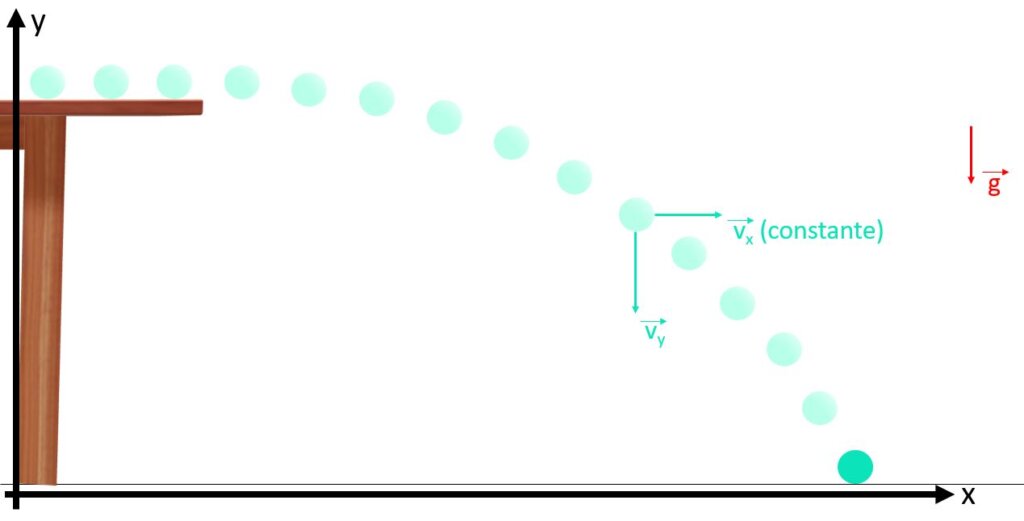
Uma dica muito importante: o movimento vertical é para baixo, então você vai precisar escolher se o sentido positivo do eixo y é para cima ou para baixo. Isso vai fazer com que alguns termos das equações levem o sinal de + ou de -.

Movimento horizontal (movimento uniforme)

Vamos analisar, primeiro, o movimento na horizontal. Ele tem a seguinte equação:

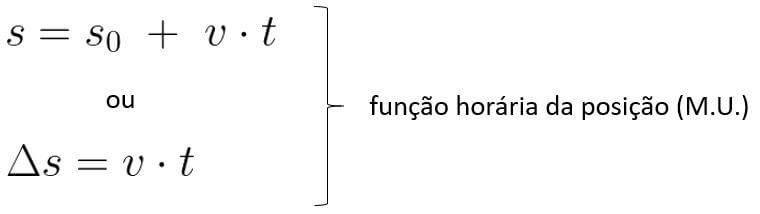
Podemos deixar essa equação com uma "cara" mais parecida com a de um lançamento horizontal. Basta chamar a variação da posição Δs de Δx. A velocidade v pode ser chamada de v_x, por ser a componente horizontal (na direção x) da velocidade. Temos então:

Movimento vertical (movimento uniformemente variado)

Agora para o movimento vertical, vamos usar as equações do movimento uniformemente variado:

Do jeito que fizemos antes, podemos mudar um pouco essas equações para que elas fiquem com a cara de um lançamento horizontal. Para isso, podemos chamar a variação da posição Δs de Δy. As velocidade v e v₀ podem ser chamadas de v_y e v_0y. Como a aceleração é a aceleração gravitacional, podemos trocar a por g:

Podemos ainda considerar v_0y igual a zero, já que no início do movimento, não havia velocidade vertical.

Tempo de queda

Um aspecto muito importante dos lançamentos horizontais é o tempo de queda do objeto, ou seja, quanto tempo ele leva, desde o lançamento, para chegar no chão. Existe uma equação própria para calcular o tempo de queda, mas antes é importante reparar em algumas coisas.

Primeiro: o tempo de queda não depende da massa do objeto, já que desprezamos a resistência do ar. Então não importa se o objeto é aerodinâmico ou não.

Segundo: o tempo de queda não depende da velocidade horizontal. A velocidade horizontal só vai contribuir para o quão longe o objeto vai (vamos ver isso logo em seguida), mas não interfere no tempo de queda. O tempo de queda só vai depender da altura de onde o objeto é lançado e da aceleração (que é a aceleração gravitacional e tem valor constante).

Para calcular o tempo de queda, usamos a seguinte equação:

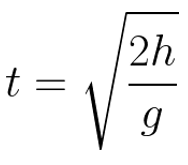
O termo h se refere à altura. Veja que essa equação não depende da massa do objeto e nem da velocidade horizontal.

Para chegar nessa equação, podemos usar a função horária da posição (do M.U.V.) e considerar a velocidade inicial (na vertical) igual a zero.

Alcance

Como vimos, a velocidade horizontal contribui para o quão longe o objeto vai chegar. Isso é chamado de alcance e, assim como o tempo de queda, costuma aparecer nas questões de vestibular.

O alcance também não depende da massa do objeto, já que estamos desprezando a resistência do ar. Ele vai depender da velocidade horizontal e da altura, já que a velocidade horizontal permite que o objeto percorra uma maior distância durante o movimento e uma maior altura permite o objeto se mover horizontalmente por mais tempo.

Podemos calcular o alcance usando a seguinte equação:

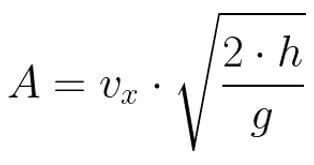
Para encontrar essa equação, usamos a função horária da posição (do M.U.). Chamamos Δx de A (o alcance) e, no lugar de t, colocamos a equação do tempo de queda.

Mas ei! O tempo de queda não foi calculado para o movimento vertical? Sim. Mas, como vimos que os dois movimentos acontecem ao mesmo tempo, o tempo de queda tem que ser o mesmo para os dois!

Quer se preparar para o Enem e vestibulares com quem mais entende do assunto?
A plataforma Aprova Total é a maior especialista no ensino digital e tem as melhores videoaulas e professores! Não deixe de conhecer os cursos Enem Hard e Super Med!