Movimento circular: princípios e aplicações

Olá, vestibulander, você sabia que movimento circular é um dos assuntos da cinemática que mais caem na prova de Física do Exame Nacional do Ensino Médio (Enem)? Neste post, ensinaremos tudo sobre o estudo do movimento circular, passando por seus princípios e aplicações.

Além disso, você terá a chance de entender tudo sobre a força centrípeta, e como ela se relaciona com outros conceitos da física. Ao final, reunimos exemplos de como o movimento circular costuma aparecer nas questões do Enem e dos principais vestibulares. E aí, vamos gabaritar Física? 😃

Introdução ao movimento circular

O movimento circular (MC) é caracterizado pela trajetória circular ou curvilínea realizada por um corpo. Para compreender melhor esse tipo de movimento, é fundamental considerar algumas grandezas importantes, como o período e a frequência.

O período, expresso em segundos (s), representa o intervalo de tempo necessário para que o corpo complete uma volta. Em outras palavras, é o tempo decorrido desde o início do movimento até o instante em que o corpo retorna exatamente à mesma posição e com a mesma direção.

Já a frequência, medida em hertz (Hz), indica o número de ciclos completos que o corpo realiza por unidade de tempo. Em outras palavras, representa quantas vezes a rotação ocorre em um segundo.
Matematicamente, o período e a frequência se relacionam:

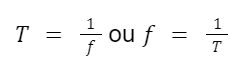
Entender as definições de período e frequência é essencial para o estudo do movimento circular. Agora, vamos aprender sobre os dois tipos de MC: o movimento circular uniforme e o movimento circular uniformemente variado.

Movimento circular uniforme (MCU)

O movimento circular uniforme é caracterizado pelo deslocamento de um corpo ao longo de uma trajetória curvilínea com velocidade constante.

Podemos observar diversos exemplos desse tipo de movimento no nosso cotidiano, como as pás do ventilador em funcionamento, o disco de vinil girando em um toca discos, as lâminas de um liquidificador em alta velocidade ou até mesmo a roda gigante em um parque de diversões quando atinge um estado estável de rotação.

Outro exemplo muito interessante de MCU é a rotação da Terra. Apesar de parecer que estamos em repouso em relação ao solo, na realidade, estamos em movimento constante de rotação.

Posição angular

A posição angular no movimento uniforme é uma medida da posição linear de um objeto em um movimento circular. Ela representa a quantidade de rotação do objeto em relação a um ponto de referência, geralmente o centro do círculo. Além disso, é expressa em radianos ou graus e varia de 0 a 2π radianos ou de 0 a 360° em uma volta completa ao redor do círculo.

Para calcular a posição angular em um movimento uniforme, utilizamos a seguinte fórmula:

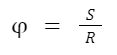
onde,

φ = ângulo (rad);

S = espaço percorrido (m);

R = raio da circunferência (m).

Deslocamento angular

No movimento circular uniforme, o deslocamento angular desempenha um papel fundamental na descrição da posição de um objeto em rotação. O deslocamento angular refere-se ao ângulo entre duas posições angulares, expresso em radianos. É calculado pela diferença entre as posições angulares inicial e final do objeto. Equivalentemente, utiliza-se:

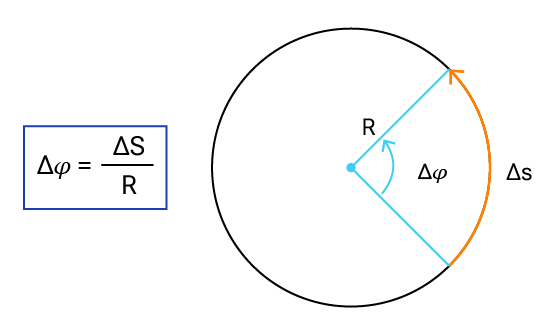
Ao contrário do deslocamento linear, que mede a distância percorrida em linha reta, o deslocamento angular considera a distância percorrida ao longo da circunferência, levando em conta a rotação.

Velocidade angular média

A velocidade angular média no movimento uniforme é uma medida da taxa média de variação do ângulo percorrido por um objeto em rotação ao longo do tempo. Podemos visualizá-la como a "velocidade de rotação" média do objeto.

Imagine-se em um carrossel: se você dá uma volta completa a cada 10 segundos, sua velocidade angular média seria de 1 volta a cada 10 segundos, ou seja, 0,1 voltas por segundo. Sendo assim, no movimento circular uniforme, a velocidade angular média é a quantidade de voltas percorridas em relação ao tempo decorrido.

É importante ressaltar que a velocidade angular média é uma grandeza escalar, medida em radianos por segundo:

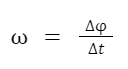
Ela nos permite compreender a rapidez com que um objeto está girando em média no decorrer de um intervalo de tempo, fornecendo uma medida quantitativa do movimento circular uniforme.

Função horária da posição do MCU

A posição do móvel no MCU pode ser dada pela fórmula:

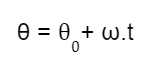
em que θ representa o ângulo no qual o corpo se encontra em determinado momento, θ₀ é o ângulo inicial do corpo na trajetória, ω é a velocidade angular e t é o tempo decorrido desde o início do movimento.

Movimento circular uniformemente variado (MCUV)

O movimento circular uniformemente variado ocorre quando um objeto se move em uma trajetória circular, mas sua velocidade angular não é constante. Isso significa que a velocidade com a qual o objeto gira ao redor do centro varia ao longo do tempo.

Aceleração angular média

A aceleração angular média no movimento circular uniformemente variado representa a taxa de variação da velocidade angular ao longo do tempo. Para entender isso de forma dinâmica, imagine-se em uma montanha-russa radicalmente emocionante:

À medida que o carrinho se aproxima de uma curva, você tem a sensação de estar grudado(a) no assento enquanto ele acelera rapidamente. Essa sensação é causada pela aceleração angular média, que está relacionada à rapidez com que o carrinho aumenta sua velocidade angular.

No entanto, quando o carrinho sai da curva e se move em uma linha reta, você perceberá uma diminuição gradual dessa sensação, indicando uma redução na aceleração angular média.

Em resumo, a aceleração angular média no movimento circular uniformemente variado contribui para a intensidade das sensações experimentadas durante o trajeto emocionante da montanha-russa.

A fórmula da aceleração angular (α) é desenvolvida a partir da variação angular da partícula:

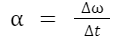
No movimento circular uniformemente variado, a aceleração angular (α) é diferente de zero, já no movimento circular uniforme, a aceleração angular será nula.

Função horária da posição e da velocidade do MCUV

A função horária do MCUV é uma fórmula matemática fundamental para descrever a posição de um objeto em movimento circular com aceleração angular constante. Ela nos permite determinar a posição angular θ de um objeto em relação ao seu ponto de partida em qualquer instante de tempo. A fórmula geralmente utilizada é:

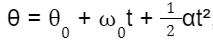
em que θ₀ é o ângulo inicial, ω₀ é a velocidade angular inicial, α é a aceleração angular constante e t é o tempo decorrido.

Com essas informações, podemos calcular a posição angular em qualquer momento do movimento.

Além da função horária da posição, a função horária da velocidade também pode ser utilizada. A função horária da velocidade no MCUV, é semelhante à função horária presente no movimento uniformemente variado (MUV), de trajetória retilínea.

Observe a seguir a fórmula que relaciona a variação angular, em radianos, com a diminuição ou aumento da velocidade angular:

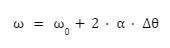
em que ω é a velocidade angular final, ω₀ é a velocidade angular inicial, α é a aceleração angular constante e Δθ é a variação angular.

Dinâmica do MCU e do MCUV

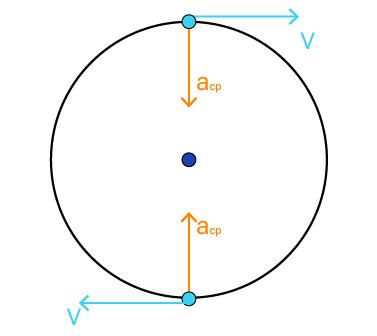
A força centrípeta desempenha um papel crucial tanto no MCU quanto no MCUV. No MCU, ela é responsável por manter um objeto em sua trajetória circular com velocidade angular constante.

Essa força se direciona para o centro da curva e é necessária para equilibrar a tendência do objeto de seguir uma trajetória em linha reta devido à sua inércia.

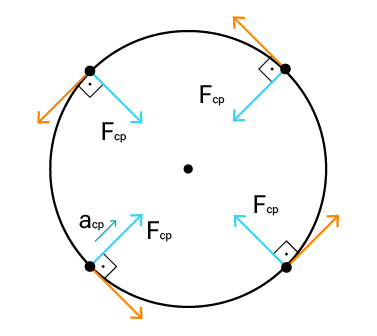
No MCUV, a força centrípeta também está presente e continua desempenhando o papel de manter o objeto na trajetória curva. No entanto, no MCUV, a velocidade angular do objeto varia, o que implica em uma aceleração angular constante.

A força centrípeta é calculada usando a fórmula:

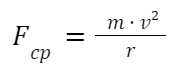
onde, F_cp é a força centrípeta, m é a massa do objeto, v é a velocidade tangencial e r é o raio da trajetória circular.

Em ambos os casos, a força centrípeta é fundamental para manter o objeto em movimento circular e é diretamente proporcional à massa do objeto e ao quadrado da velocidade tangencial.

Como o movimento circular aparece no Enem e vestibulares?

Movimento circular é um tema muito presente no Enem e vestibulares. Por se tratar de um assunto com inúmeras aplicações, o movimento circular costuma cair nas provas em questões práticas e interdisciplinares ou em questões bem conceituais.

Se liga nos exemplos que trouxemos para você praticar e bons estudos!

Exercício 1

(Enem) Um professor utiliza essa história em quadrinhos para discutir com os estudantes o movimento de satélites. Nesse sentido, pede a eles que analisem o movimento do coelhinho, considerando o módulo da velocidade constante.

Desprezando a existência de forças dissipativas, o vetor aceleração tangencial do coelhinho, no terceiro quadrinho, é

a) nulo.
b) paralelo à sua velocidade linear e no mesmo sentido.
c) paralelo à sua velocidade linear e no sentido oposto.
d) perpendicular à sua velocidade linear e dirigido para o centro da Terra.
e) perpendicular à sua velocidade linear e dirigido para fora da superfície da Terra.

Resposta: [A]
Como o módulo da velocidade é constante, o movimento do coelhinho é circular e uniforme, sendo nulo o módulo da componente tangencial da aceleração no terceiro quadrinho.

Exercício 2

Em abril de 2021 faleceu o astronauta norte-americano Michael Collins, integrante da missão Apolo 11, que levou o primeiro homem à Lua. Enquanto os dois outros astronautas da missão, Neil Armstrong e Buzz Aldrin, desceram até a superfície lunar, Collins permaneceu em órbita lunar pilotando o Módulo de Comando Columbia.

(Unicamp) A órbita do Columbia era aproximadamente circular, e o módulo da aceleração gravitacional na órbita era A força resultante centrípeta é desempenhada pela força gravitacional exercida pela Lua, ou seja, Sendo o módulo da velocidade do Columbia qual foi aproximadamente o período T da órbita?

a) T = 20 min.
b) T = 2,0 h.
c) T = 3,0 h.
d) T = 4,0 h.

Resposta: [B]
A aceleração da gravidade na órbita é a própria aceleração centrípeta.

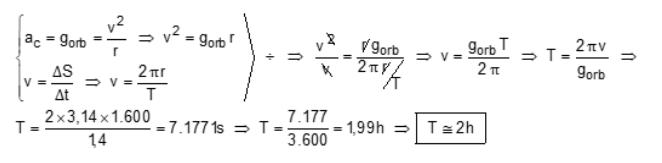
Exercício 3

(Ufrgs) Considere, na figura abaixo, a representação de um automóvel, com velocidade de módulo constante, fazendo uma curva circular em uma pista horizontal.

Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem em que aparecem.

A força resultante sobre o automóvel é ___________e, portanto, o trabalho por ela realizado é ___________.

a) nula – nulo
b) perpendicular ao vetor velocidade – nulo
c) paralela ao vetor velocidade – nulo
d) perpendicular ao vetor velocidade – positivo
e) paralela ao vetor velocidade – positivo

Resposta: [B]
No movimento circular uniforme, a velocidade tem módulo constante, mas direção e sentido estão mudam devido à existência de força resultante centrípeta perpendicular ao vetor velocidade e ao vetor deslocamento. Sendo assim, o trabalho da força resultante será nulo, já que quando a força é perpendicular ao deslocamento esta força não realiza trabalho.

Quer preparação máxima para ter alto rendimento no Enem e vestibulares e ingressar no curso dos seus sonhos? Venha estudar com o Aprova Total e garanta a sua vaga na universidade!