Fluidos: características, teoremas e exercícios

Uma palavra tão curtinha, como "fluidos", traz consigo diversas informações, sabia? Ela está presente em muitas questões de Física, e é um dos assuntos mais cobrados desse componente no Exame Nacional do Ensino Médio (Enem). Para ajudar você a mandar bem e resolver os exercícios de maneira confiante, reunimos tudo o que é importante saber sobre os fluidos. Vamos lá? 😉

O que são fluidos?

Os fluidos são substâncias que possuem a capacidade de fluir e se deformar quando submetidas a uma força externa. Eles são compostos por partículas que se movimentam livremente e não possuem uma estrutura rígida definida, como sólidos. Os fluidos podem ser encontrados em diferentes estados físicos, como líquidos e gases.

Os líquidos têm uma densidade maior e uma coesão intermolecular mais forte, resultando em formas definidas, mas que se adaptam ao formato do recipiente. Por outro lado, os gases têm menor densidade e são altamente compressíveis, preenchendo completamente o volume do recipiente.

O estudo dos fluidos é essencial em diversas áreas da ciência e da engenharia, como a hidrostática, a hidrodinâmica e a aerodinâmica, permitindo compreender o comportamento e as propriedades dessas substâncias em diferentes situações, desde o fluxo de água em rios até a propulsão de foguetes.

No contexto do vestibular, é fundamental compreender as características dos fluidos para resolver problemas relacionados a esses conceitos e aplicá-los de forma adequada em questões de Física, Química e mais.

👉 Leia também:

Soluções químicas: o que estudar para o Enem?

Principais características de um fluido

No estudo da Física, usamos os fluidos ideais, que são modelos teóricos com características específicas e simplificadas. Em um fluido ideal, considera-se que não há viscosidade, ou seja, não há resistência interna ao movimento das partículas.

Além disso, um fluido ideal é incompressível, ou seja, sua densidade permanece constante independentemente da pressão exercida sobre ele. Outra característica dos fluidos ideais é que eles seguem as leis de conservação da massa e da energia de forma perfeita.

No entanto, na prática, os fluidos reais não possuem todas essas limitações. Fluidos reais possuem viscosidade, que é a resistência interna ao fluxo, resultando em perdas de energia térmica. Eles podem sofrer ainda de compressibilidade em determinadas condições, alterando sua densidade. Mas essas especificações serão muito importantes apenas se você se especializar na área.

Densidade e massa específica

A densidade é uma propriedade física que relaciona a massa de um corpo à quantidade de espaço que ele ocupa. Ela é definida como a razão entre a massa desse corpo e o seu volume.

ρ = m/V

A densidade, no SI, é expressa em unidades de massa por unidade de volume, como quilograma por metro cúbico (kg/m³).

Essa é uma medida importante para comparar a "concentração" de massa em diferentes corpos. Corpos mais densos têm uma maior concentração de massa em um dado volume, enquanto corpos menos densos têm menor concentração de massa.

Por outro lado, temos a massa específica, uma medida relacionada à densidade, que se refere à massa por unidade de volume de uma substância pura. Ela é uma propriedade intrínseca de cada substância, independentemente de sua forma ou estado físico.

A principal diferença entre densidade e massa específica é que a densidade pode variar dependendo da composição ou presença de impurezas, enquanto a massa específica é uma propriedade única e constante para cada substância.

No Enem e nos vestibulares, é essencial ter conhecimento da densidade da água, em temperatura ambiente, como uma referência importante. A densidade da água é de aproximadamente 997 kg/m³ ou, frequentemente utilizada, 1 g/cm³.

Pressão hidrostática x pressão atmosférica: qual a diferença?

Vamos começar pelo básico: o que é pressão? A pressão é uma grandeza física que descreve a força exercida por uma substância sobre uma determinada área. Ela pode ser definida como a razão entre a força aplicada em uma superfície e a área dessa superfície.

P = F/A

A pressão é expressa em unidade de força por unidade de área, sendo newton por metro quadrado (N/m²), que também podemos chamar de pascal (Pa).

A pressão hidrostática é a pressão exercida por um fluido em repouso devido à gravidade. Ela depende da altura do fluido e de sua densidade. Quanto maior a altura do fluido, maior será a pressão hidrostática exercida na base.

A pressão exercida por um líquido é precisamente o produto da densidade pela aceleração gravitacional e pela altura.

P = ρ ⋅ g ⋅ h

Onde P é a pressão (Pa), ρ é a densidade (kg/m³), g a aceleração da gravidade (m/s²) e h é a altura (m).

Exemplo: o caso das girafas

Uma curiosidade é o caso das girafas: agora que você conhece a definição de pressão, já imaginou o quanto de pressão uma girafa precisa ter para bombear sangue para o cérebro, devida à sua altura?

A dependência da pressão em um líquido com a profundidade não é problema para a girafa, por causa de seu grande coração e do intricado sistema de válvulas e vasos sanguíneos absorventes e elásticos no cérebro. Sem tais estruturas, ela desmaiaria quando erguesse subitamente a cabeça e estaria sujeita a hemorragia cerebral quando a abaixasse.

Já pressão atmosférica é a pressão exercida pelo ar na superfície terrestre devido ao peso da coluna de ar acima dela. Ela diminui com o aumento da altitude, pois a quantidade de ar diminui. Ao nível do mar, a pressão atmosférica média é de aproximadamente 1 atm (atmosfera), equivalente a 101325 Pa.

A pressão atmosférica tem influência em diversos aspectos, como fenômenos meteorológicos, formação de nuvens e ventos, previsão do tempo e a utilização de barômetros para determinar mudanças na altitude.

Teorema de Stevin e os fluidos

O teorema de Stevin, também conhecido como princípio de Stevin ou lei de Stevin, é um importante resultado na hidrostática que descreve a relação entre a pressão em um fluido e a altura do fluido em um recipiente aberto.

Esse teorema estabelece que a diferença de pressão entre dois pontos em um fluido em repouso é diretamente proporcional à diferença de altura vertical entre esses pontos, considerando-se a densidade do fluido.

ΔP = ρ ⋅ g ⋅ Δh

Onde ρ é pressão manométrica ou variação de pressão, medida em pascal (Pa), ρ é a densidade (kg/m³), g é a aceleração da gravidade (m/s²) e h é a altura (m). Em outras palavras, quanto maior a altura de uma coluna de fluido, maior será a pressão exercida pela coluna sobre um ponto inferior.

Esse teorema é aplicado em diversas situações, como em sistemas de tubulações, vasos comunicantes e barragens. Por exemplo, em um sistema de tubulações, a pressão em um ponto mais baixo será maior do que a pressão em um ponto mais alto, devido à diferença de altura entre os pontos.

Esse princípio é fundamental para entender o funcionamento de dispositivos como o barômetro, utilizado para medir a pressão atmosférica, e o manômetro, utilizado para medir a pressão em sistemas fechados.

Resumo: o que você precisa saber sobre fluidos

Para o Enem, você não pode deixar de estudar a definição de densidade e pressão:

• a densidade refere-se à concentração de massa em relação ao volume de uma substância. É uma propriedade física que descreve a "compactação" de um material e é expressa em unidades como kg/m³ ou g/cm³.

ρ = m/V

• já a pressão é a força exercida por uma substância em uma determinada área. Ela é calculada dividindo a força pela área e é medida em unidades como pascal (Pa) ou atm.

P = F/A

É importante também entender o conceito por trás do Teorema de Stevin:

• ele estabelece que a diferença de pressão entre dois pontos de um fluido em repouso é diretamente proporcional à diferença de altura entre esses pontos, considerando a densidade do fluido.

ΔP = ρ ⋅ g ⋅ Δh

O teorema costuma aparecer em questões mais diretas, envolvendo tubulações residenciais e experimentos simples, onde você deverá analisar o que acontece com a pressão aumentando ou diminuindo a altura.

👉 Leia também:

Introdução à óptica: entenda os principais conceitos

Lei da Gravitação Universal: veja conceitos e fórmulas

Exercícios de Física sobre fluidos

Que tal agora você colocar em prática os conhecimentos vistos até aqui?

Exemplo 1

(Enem 2021)

TEXTO I

No cordel intitulado Senhor dos Anéis, de autoria de Gonçalo Ferreira da Silva, lê-se a sextilha:

A distância em relação
Ao nosso planeta amado
Pouco menos que a do Sol
Ele está distanciado
E menos denso que a água
Quando no normal estado

MEDEIROS, A.; AGRA, J. T. M., A astronomia na literatura de cordel. Física na Escola, n. 1, abr, 2010 (fragmento).

TEXTO II

Distâncias médias dos planetas ao Sol e suas densidades médias

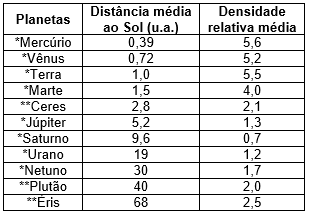
Características dos planetas. Disponível em: www.astronoo.com. Acesso em: 8 nov. 2019 (adaptado).

Considerando os versos da sextilha e as informações da tabela, a qual planeta o cordel faz referência?

a) Mercúrio.   

b) Júpiter.   

c) Urano.   

d) Saturno.   

e) Netuno.   

Resposta: [D]
A densidade relativa é a densidade do corpo em relação à água. O cordel faz referência a um planeta de densidade relativa menor que a da água (menor que 1 g/cm³). Consultando a tabela, nota-se que o único planeta com essa característica é Saturno.

Exemplo 2

(Enem 2020) Um mergulhador fica preso ao explorar uma caverna no oceano. Dentro da caverna formou-se um bolsão de ar, como mostrado na figura, onde o mergulhador se abrigou.

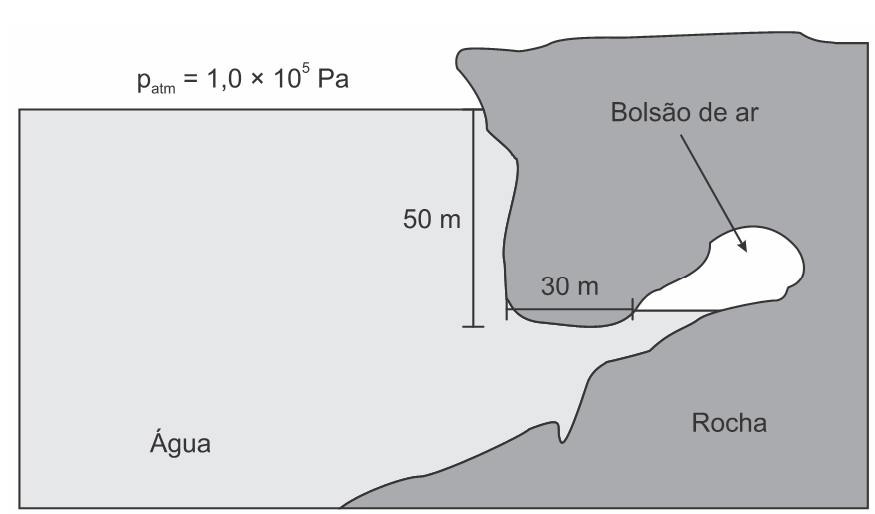
Durante o resgate, para evitar danos a seu organismo, foi necessário que o mergulhador passasse por um processo de descompressão antes de retornar à superfície para que seu corpo ficasse novamente sob pressão atmosférica. O gráfico mostra a relação entre os tempos de descompressão recomendados para indivíduos nessa situação e a variação de pressão.

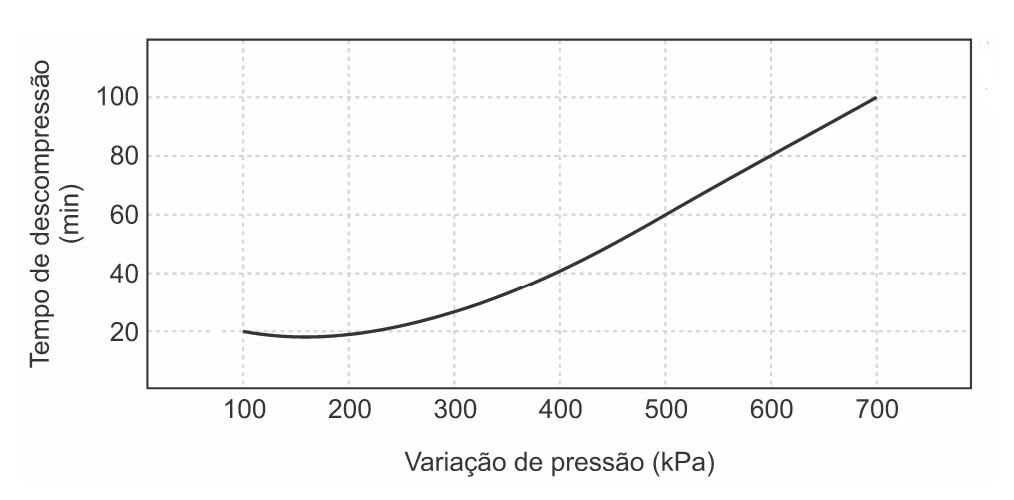
Considere que a aceleração da gravidade seja igual a 10m.s^-2 e que a densidade da água seja de ρ = 1000 kg.m^-3.

Em minutos, qual é o tempo de descompressão a que o mergulhador deverá ser submetido?
a) 100
b) 80
c) 60
d) 40
e) 20

Resposta: [C]
O aumento de pressão a que ele foi submetido é devido a pressão da coluna do fluido.

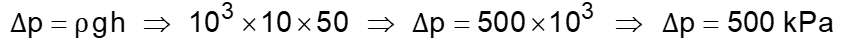
Analisando o gráfico, para o aumento de pressão, o tempo de descompressão deve ser de 60 minutos.