Hidrodinâmica: veja princípios, fórmulas e exercícios
Vamos explicar os conceitos mais importantes dessa área e preparar você para questões que podem cair no Enem e outros vestibulares

Acessibilidade
Você já se perguntou como um avião se sustenta no ar, mesmo sendo tão pesado? Por que a água sai mais rapidamente quando tapamos parte da ponta de uma mangueira? Qual é a função do aerofólio de um carro de Fórmula 1? Apesar de serem situações muito diferentes, todas elas são explicadas por conceitos de hidrodinâmica, a área da Física que estuda fluidos em movimento.

A seguir, vamos explicar os conceitos mais importantes dessa área e demonstrar como o Exame Nacional do Ensino Médio (Enem) e os vestibulares cobram o assunto.
NAVEGUE PELOS CONTEÚDOS
Qual a diferença entre hidrostática e hidrodinâmica?
Tanto a hidrostática quanto a hidrodinâmica estudam fluidos, substâncias capazes de fluir ou escoar. É o caso de líquidos e de gases. Mas, enquanto a hidrostática estuda fluidos em equilíbrio, a hidrodinâmica não, ou seja, há escoamento de fluidos.
Quando calculamos a pressão que a água exerce sobre um mergulhador, a força que precisamos aplicar para uma máquina hidráulica erguer um veículo e ao analisar se um corpo afunda ou flutua em um líquido, estamos lidando com hidrostática.
Por outro lado, situações como calcular o tempo que uma mangueira leva para encher a piscina, o estudo da circulação sanguínea e de corpos se movendo em um fluido são casos de escoamento, ou seja, entra em jogo a hidrodinâmica.
No acidente envolvendo o submarino Titan, por exemplo, podemos usar a hidrostática para fazer o cálculo da imensa pressão exercida por quilômetros de água acima dele. Porém, após a implosão, é preciso usar conceitos de hidrodinâmica, por causa do fluxo de água que existe de fora para dentro do submarino, devido à diferença de pressão.

Principais conceitos de hidrodinâmica
Para compreender bem o que é hidrodinâmica, vamos estudar os conceitos mais importantes, bem como os seus significados.
Fluido ideal
Na hidrodinâmica, nós trabalhamos com um modelo de fluido ideal. As características de um fluido ideal são as seguintes:
- incompressível
mesmo exercendo forças sobre o fluido, não é possível alterar seu volume. Líquidos em geral são, de fato, pouco compressíveis. - não viscoso
viscosidade é a característica que um fluido tem de haver atrito entre suas camadas durante um escoamento. Se você comparar água e mel escorrendo por uma parede, vai perceber que o mel será bem mais lento do que a água, pois ele é mais viscoso. Um modelo de fluido ideal não possui viscosidade. - escoamento estacionário
se analisarmos um mesmo ponto no escoamento de um fluido, a velocidade do fluido nesse ponto será sempre a mesma.

Veja que interessante o GIF acima: parece que a água está "congelada", certo? Mas, se olharmos o contato dela com o chão e a tocarmos, veremos que ela está fluindo. O escoamento é tão regular que toma um caráter estacionário, dando a impressão de que não há fluxo de água.
Vazão
A vazão (Z) corresponde à razão entre o volume de fluido (ΔV) que atravessa uma certa região e o intervalo de tempo (Δt) decorrido nesse escoamento. A fórmula para calcular vazão é
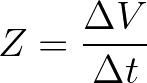
Logo, para um mesmo Δt, quanto mais fluido (maior ΔV) atravessar a região, maior será a vazão. De maneira semelhante, se compararmos duas torneiras abertas, a que encher primeiro (menor Δt) um mesmo balde (mesmo ΔV) terá a maior vazão.
Como vazão corresponde à razão entre volume e tempo, então sua unidade no Sistema Internacional é o metro cúbico por segundo (m³/s).
Sobre hidrodinâmica, o Enem cobra, basicamente, vazão! De 2009 para cá, foram sete questões (incluindo Enem Regular e PPL) sobre esse assunto. Em um exercício do Enem PPL de 2021, foi preciso considerar a fórmula da vazão escrita de uma outra forma, como veremos nos exemplos.
Fórmula da vazão usando a velocidade de escoamento
Na imagem abaixo, um volume ΔV de fluido atravessa uma região de um tubo cilíndrico cuja área de secção transversal é A. Essa porção de fluido atravessa o tubo com velocidade v.
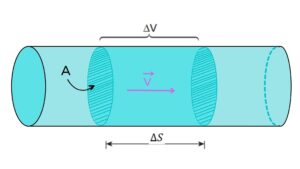
Veja que, por ser um tubo cilíndrico, podemos representar o volume ΔV por ΔV = A · ΔS. Logo, é possível reescrever nossa fórmula da vazão como
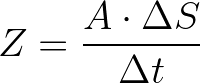
Com essa nova "cara" para a fórmula da vazão, podemos perceber que o termo ΔS/Δt corresponde à velocidade v de escoamento do fluido, o que nos leva à seguinte versão da fórmula:
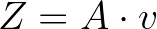
Unidades de volume
Nas questões de vazão, é muito comum aparecerem diferentes unidades de medidas envolvendo volume. E é claro que o Aprova também vai ajudar nisso! Confira algumas conversões das unidades de volume:
1 L = 1.000 mL = 1 dm3 = 10-3 m3
Juntamente com essas relações, é útil lembrar que, como 1 L = 10-3 m3, então 1 m3 = 1.000 L.
Vazão mássica
Às vezes, utiliza-se o termo "vazão mássica" para se referir ao conceito de vazão, mas considerando uma quantidade de massa, e não de volume, atravessando uma certa região. Para distinguir da definição que vimos anteriormente, a vazão que utiliza o volume é também chamada de "vazão volumétrica".
Como a vazão mássica corresponde à razão entre massa e intervalo de tempo, sua unidade no Sistema Internacional é o quilograma por segundo (kg/s).
Equação da continuidade
Observe a figura abaixo, em que um fluido atravessa, da esquerda para a direita, um tubo que afunila em uma determinada região.
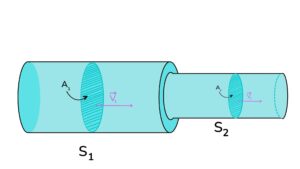
É visível que a área A1 é maior do que a área A2. No entanto, todo o fluido que atravessar A1 deverá atravessar A2, pois a matéria não "desaparece", de acordo com o princípio de conservação da massa. Portanto, as vazões em A1 e em A2 devem ser iguais:
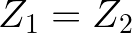
Nesse sentido, podemos substituir as vazões Z1 e Z2 pelas expressões que obtivemos da vazão usando a velocidade de escoamento:
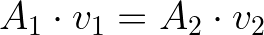
Essa é a equação da continuidade. Ela nos mostra que, se a área diminui, a velocidade deve aumentar para manter constante a vazão, e vice-versa.
É exatamente isso que explica por que a água sai mais veloz quando cobrimos parte da mangueira com o dedo: como a vazão tem que ser constante, se diminuímos a área, a velocidade de escoamento aumenta. Em outras palavras, como a vazão é constante, área e velocidade são inversamente proporcionais.

Se considerarmos que a profundidade é a mesma em toda a região, a velocidade da correnteza do rio na foto abaixo é maior nas partes mais estreitas do que nas partes mais largas. Isso também é uma consequência da equação da continuidade.

Equação/princípio de Bernoulli
Daniel Bernoulli (1700-1782), membro de uma notável família de matemáticos, teve grande importância no estudo da hidrodinâmica. De maneira simplificada, o princípio de Bernoulli explica que, para um fluido em escoamento, a pressão diminui se a velocidade aumenta.
Matematicamente, podemos analisar esse fenômeno a partir da equação de Bernoulli, que relaciona as seguintes grandezas de um fluido: pressão (p), altura (h, de acordo com um referencial) e velocidade de escoamento (v). A equação de Bernoulli é a seguinte:
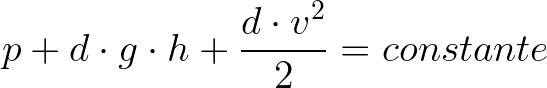
O termo d se refere à densidade do fluido e g é a aceleração gravitacional. O fato de a soma dos termos dessa equação ser constante nos permite escrever de outra forma, relacionando duas situações no escoamento de um fluido. Exemplo: uma região mais larga e uma região mais estreita, situadas em diferentes níveis de altura de um cano:
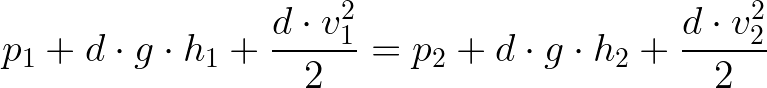
Isso significa que a soma p + d · g · h + (d · v²)/2 é sempre a mesma, não importa a região do fluido que estivermos analisando.
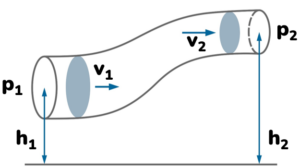
A formulação da equação de Bernoulli decorre do princípio de conservação da energia.
Casos específicos da equação de Bernoulli
As duas equações que vimos anteriormente correspondem à expressão mais geral da equação de Bernoulli. Podemos, no entanto, obter equações mais específicas para algumas situações.
Pontos a uma mesma altura em um fluido em movimento
Caso estejamos considerando dois pontos a uma mesma altura h, por exemplo, veja que ambos os lados da equação terão os termos d · g · h iguais, podendo ser simplificados, o que nos leva à equação
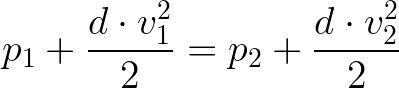
Note que essa não é uma "fórmula nova", é a boa e velha equação de Bernoulli. A diferença é que foi possível simplificar um termo de ambos os lados da equação, então ela ficou menor.
Essa fórmula permite enxergar o que vimos de início sobre a equação de Bernoulli:
- se a velocidade diminui, a pressão aumenta (e vice-versa);
- a partir do efeito acima e da equação da continuidade, podemos concluir que, se a velocidade diminui, a área é maior e a pressão é maior.
Mas pressão e área não são inversamente proporcionais? Afinal, P = F/A, não? Então, como pode a pressão ser maior quanto maior for a área?
Tenha cuidado! Essa é uma dúvida muito comum. Na fórmula P = F/A, pressão e área somente serão inversamente proporcionais caso a força F seja constante.
Esse efeito de a velocidade diminuir e a pressão aumentar quando um fluido atravessa uma região de maior área (bem como a velocidade aumentar e a pressão diminuir se atravessar uma região de menor área) é conhecido como efeito Venturi.
Pontos em um fluido em repouso
A equação de Bernoulli é tão poderosa que descreve até mesmo uma situação de hidrostática. Imagine dois pontos quaisquer de um fluido em repouso. Como ele está em repouso, suas velocidades são nulas nesses dois pontos. Logo, o termo (d · v²)/2 é nulo em ambos os lados da equação, restando somente isso:
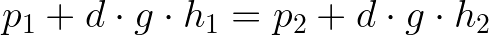
Se manipularmos um pouco essa equação, podemos obter a forma p1 - p2 = d · g · h2 - d · g · h1. Como d e g são constantes, podemos colocar esses termos em evidência, portanto teremos p1 - p2 = d · g · (h2 - h1). Chamando p1 - p2 de Δp e chamando h2 - h1 de Δh, a equação terá a forma
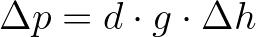
Se você tem a impressão de que ela é familiar, é porque provavelmente já a viu mesmo! Essa é a expressão do teorema de Stevin, que estudamos lá na hidrostática.
Podemos ir além: se não houver diferença de altura, Δh = 0, logo, Δp = 0. Isso significa que, para pontos em uma mesma altura de um fluido em repouso, as pressões são as mesmas - outra informação que já sabíamos da hidrostática!
Consequências do princípio de Bernoulli
A partir de tudo o que aprendemos até agora, é possível explicar diversos fatos interessantes do dia a dia.
Por que aviões voam?
Afinal, como um avião, sendo tão imenso e pesado, consegue voar, desafiando a gravidade?
As asas são fabricadas com design aerodinâmico, tendo como resultado uma passagem do ar com velocidade maior no topo da asa e menor no inferior da asa. Lembra que a pressão é maior para um fluido mais lento? Assim, diferença de pressão possibilita uma força de sustentação, de baixo para cima, que impede o avião de cair.
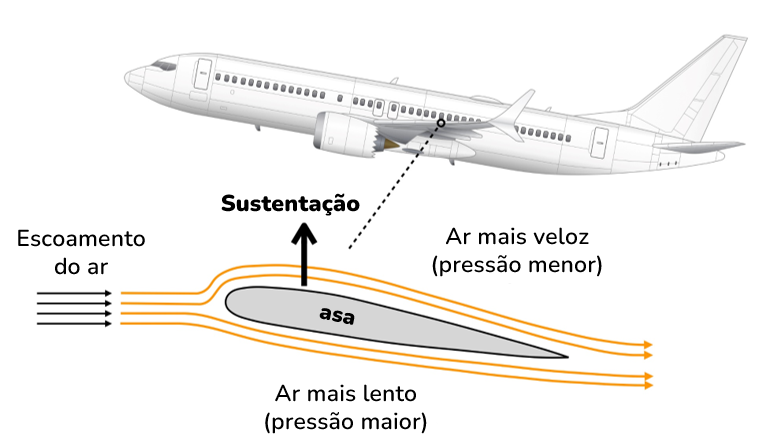
Para que serve um aerofólio?
Carros de corrida, como os de Fórmula 1, por exemplo, precisam de uma grande força de atrito com a pista para evitar que os pneus percam contato com o chão e levem o veículo a capotar. Sabemos que um atrito intenso requer uma força normal intensa. Assim, é preciso que o veículo pressione o chão com força e, para isso, ele utiliza aerofólios.
Você pode pensar em um aerofólio como uma "asa de avião invertida", ou seja, a velocidade do ar é menor na parte superior do que na parte inferior do aerofólio. Dessa forma, a pressão será maior em cima, pressionando o veículo contra a pista.

Destelhamentos e cortinas
As diferenças de pressão nos fluidos em movimento podem provocar destelhamentos em casas. Quando o vento passa sobre o telhado, reduz a pressão e, caso a pressão no interior da casa seja suficientemente maior, ocorrerá o destelhamento.
Uma situação semelhante, porém menos agressiva, ocorre quando uma cortina escapa para fora da janela em um dia de muitos ventos. Como os ventos reduzem a pressão na parte de fora, a pressão superior interna "expulsa" a cortina pela janela.

Você pode, aliás, verificar um efeito semelhante a partir de um experimento caseiro muito simples:
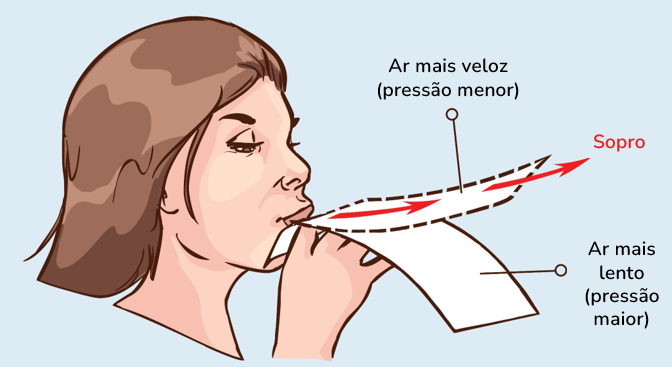
segure uma folha de papel pelo lado menor; em seguida, assopre como na imagem abaixo.
Isso fará com que a folha, antes curvada para baixo, suba por conta da diferença de pressão na parte de cima (velocidade maior, pressão menor) e na parte de baixo (velocidade menor, pressão maior).
Resumo: conceitos da hidrodinâmica
Vamos relembrar os conceitos mais importantes que vimos até aqui sobre hidrodinâmica?
- fluido ideal
modelo de fluido utilizado nos estudos de hidrodinâmica. Um fluido ideal tem as seguintes características: é incompressível, não viscoso e tem escoamento estacionário. - vazão
grandeza que corresponde à razão entre o volume (ΔV) de fluido que atravessa uma região e o intervalo de tempo (Δt) em que essa porção de fluido o atravessa. Também pode ser calculada pelo produto da área (A) de secção transversal da região e da velocidade (v) de escoamento: Z = ΔV/Δt = A · v (tome cuidado para não confundir o V de volume com o v de velocidade). - equação da continuidade
entre duas regiões, 1 e 2, de escoamento de um fluido ideal, a vazão é constante, o que nos leva à relação A1 · v1 = A2 · v2 - equação de Bernoulli
em sua forma completa, a soma p + d · g · h + (d · v²)/2 é a mesma para qualquer ponto do fluido. O termo p é a pressão, g é a aceleração gravitacional, d é a densidade do fluido e h é a altura.

Exercícios resolvidos de hidrodinâmica do Enem e vestibulares
Ufa! Aprendemos, enfim, sobre os tópicos mais importantes de hidrodinâmica. Que tal agora dar uma olhada em como o Enem e os vestibulares cobram esses assuntos?
A hidrodinâmica é um assunto mais comum em vestibulares militares, mas, às vezes, dá as caras em outras provas. Como vimos anteriormente, até hoje, o Enem só cobrou questões de hidrodinâmica envolvendo a ideia de vazão.
Exemplo 1 - Vazão
(Enem PPL 2021) Para gerar energia elétrica em uma hidrelétrica é necessário integrar a vazão do rio, a quantidade de água disponível em determinado período de tempo e os desníveis do relevo, sejam eles naturais, como as quedas-d’água, ou criados artificialmente. Existem dois tipos de unidades de geração de energia: acumulação e fio-d’água. As unidades de acumulação são localizadas em locais com altas quedas-d’água e, dado o seu grande porte, permitem o acúmulo de grande quantidade de água. As unidades a fio-d’água geram energia com o fluxo de água do rio, ou seja, pela vazão com mínimo ou nenhum acúmulo do recurso hídrico. Em uma região existem rios com potencial para geração de energia. No intuito de construir uma unidade de fio-d’água, deve-se comparar as características desses rios.
Atlas de energia elétrica do Brasil. Disponível em: www.fisica.net. Acesso em: 4 dez. 2018 (adaptado).
A principal grandeza física desses rios que deve ser observada é o(a)
a) velocidade de correnteza maior.
b) deslocamento vertical do relevo maior.
c) área de secção transversal do leito menor.
d) volume de água por unidade de tempo menor.
e) quantidade de massa de água por unidade de tempo menor.
Resposta: [A]
"De cara", podemos perceber que a alternativa A é a correta, pois o enunciado diz que é necessário integrar a vazão do rio (...) e os desníveis do relevo, e aprendemos que vazão pode ser calculada por Z = A · v. Como é necessária uma grande vazão para obter uma maior quantidade de energia, então é interessante que haja uma maior velocidade de correnteza.
Exemplo 2 - Equação da continuidade
(Unicamp 2017) A microfluídica é uma área de pesquisa que trabalha com a manipulação precisa de líquidos em canais com dimensões submilimétricas, chamados de microcanais, possibilitando o desenvolvimento de sistemas miniaturizados de análises químicas e biológicas.
Considere que uma seringa com êmbolo cilíndrico de diâmetro D = 4 mm seja usada para injetar um líquido em um microcanal cilíndrico com diâmetro de d = 500 μm. Se o êmbolo for movido com uma velocidade de V = 4 mm/s, a velocidade v do líquido no microcanal será de:
a) 256,0 mm/s.
b) 32,0 mm/s.
c) 62,5 μm/s.
d) 500,0 μm/s.
Resposta: A
Como o êmbolo e o microcanal são cilíndricos, suas áreas de secção transversais são áreas de circunferências, que podemos calcular por A = π · r². O enunciado pede que calculemos a velocidade v no microcanal, então podemos usar a equação da continuidade para determinar as áreas A (do êmbolo) e a (do microcanal) e sabemos a velocidade V no êmbolo:
A · V = a · v
π · (4/2)² · 4 = π · (0,5/2)² · v (perceba que usamos o diâmetro d = 500 μm em mm)
Podemos simplificar os π de ambos os lados da equação:
4 · 4 = (0,25/4) · v (ao invés de dividir 0,5 por 2 e elevar ao quadrado, é interessante manter na forma de fração, pois possibilita simplificações)
16 = 0,25v/4
64 = 0,25v
v = 64/0,25
v = 256 mm/s

