Segunda lei da termodinâmica: conceitos e fórmulas
Confira o que é a Segunda Lei da Termodinâmica, quais as suas aplicações em máquinas térmicas e entenda o conceito de entropia

Acessibilidade
A segunda Lei da termodinâmica é uma das bases da termodinâmica, a área da física que estuda as relações existentes entre energia térmica e energia mecânica.
De acordo com a primeira lei da termodinâmica, sabemos que calor pode ser transformado em trabalho (e vice-versa) através de diversos processos. Mas será que existem restrições para esse tipo de processo? Para responder a essa pergunta, vamos olhar para outra lei.
A segunda lei da termodinâmica pode ser expressa de diversas formas. No entanto, todas elas são equivalentes e nos apresentam as restrições existentes nos processos termodinâmicos.
Primeiro, vamos conhecer uma das principais aplicações da termodinâmica: as máquinas térmicas.
NAVEGUE PELOS CONTEÚDOS
Máquinas térmicas e a segunda lei da termodinâmica
Chamamos de máquina térmica qualquer dispositivo capaz de converter calor em trabalho útil. Em geral, as máquinas térmicas operam em ciclos, conhecidos como ciclos termodinâmicos.
Alguns exemplos comuns de máquinas térmicas são as máquinas a vapor (utilizadas em trens e navios), os motores de automóveis e até mesmo os reatores nucleares.
Vamos usar como exemplo um motor de automóvel. No interior desse motor ocorre uma reação de combustão envolvendo um combustível (gasolina, por exemplo). Essa reação é extremamente exotérmica, ou seja, libera muito calor. A principal função do motor é converter esse calor em trabalho útil, que é o que proporciona a tração nas rodas e, consequentemente, o movimento do automóvel.
Tá, mas será que todo o calor gerado pela combustão é convertido em trabalho útil? A resposta é não! Para entender o porquê disso, precisamos nos voltar para a segunda lei da termodinâmica.
O primeiro enunciado da segunda lei da termodinâmica que iremos estudar é o enunciado de Kelvin-Planck:
"É impossível construir uma máquina que, operando em ciclos termodinâmicos, tenha como único efeito converter integralmente em trabalho todo o calor recebido."
Parece complicado, né?! Mas, na verdade, é bem simples. Esse enunciado nos diz que nenhuma máquina térmica é capaz de transformar em trabalho todo o calor que recebe.
Sendo assim, podemos concluir também que, para toda máquina térmica, parte do calor recebido (aquele que não foi convertido em trabalho) é rejeitado durante o processo. No nosso exemplo dos automóveis, esse calor rejeitado deixa a máquina através do sistema de escapamento.
Conservação da Energia em Máquinas Térmicas
Podemos nos utilizar do princípio da conservação da energia para relacionar o calor recebido (Q₁), o calor rejeitado (Q₂) e o trabalho útil (τ) gerado por uma máquina térmica da seguinte maneira:

Ou seja, o trabalho útil gerado por uma máquina térmica é equivalente à quantidade de calor recebida menos a quantidade de calor rejeitada.
Observe no esquema abaixo um resumo do funcionamento de qualquer máquina térmica:
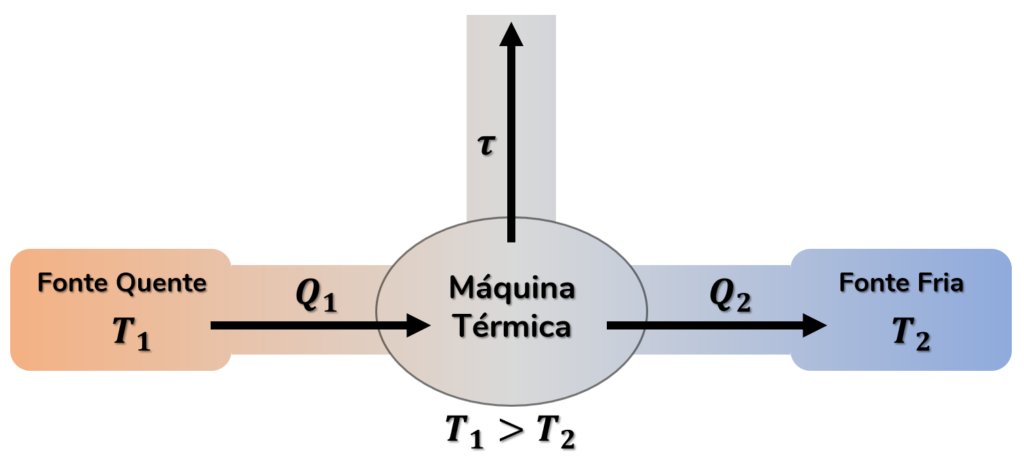
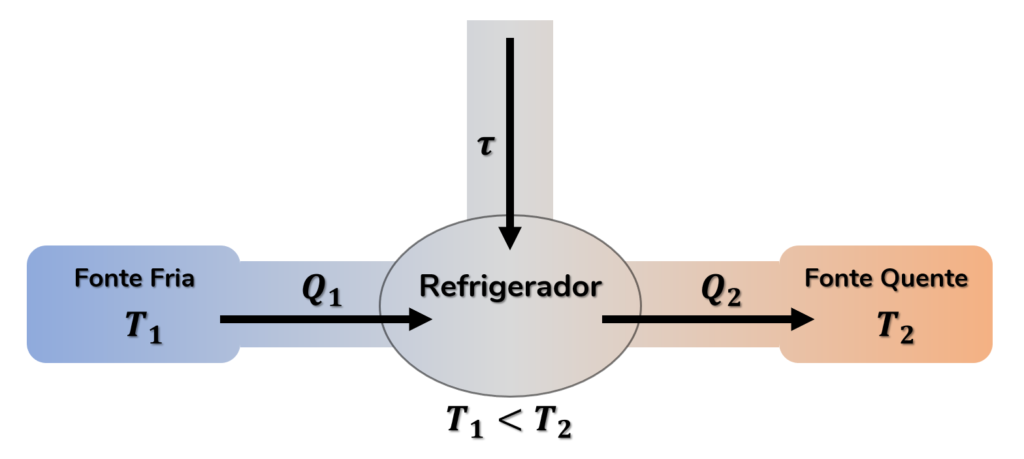
Note que chamamos de fonte quente a região que fornece o calor à máquina. Já a fonte fria é a região para onde o calor é rejeitado. É importante lembrar que, para toda máquina térmica, a temperatura (T₁) da fonte quente é maior do que a temperatura (T₂) da fonte fria.
Rendimento das máquinas térmicas
Para entender a eficiência de uma máquina térmica, utilizamos um índice chamado de rendimento.
O rendimento (η) nos diz o quanto um dispositivo é eficiente em transformar calor em trabalho útil. Na teoria, esse índice pode variar entre 0 e 1. Nesse sentido, 1 é para um dispositivo que converte em trabalho 100% do calor recebido e 0 para um dispositivo incapaz de gerar trabalho.
No entanto, aprendemos que nenhuma máquina térmica é capaz de converter calor integralmente em trabalho. Por isso, podemos concluir que não existe e nem existirá máquina térmica com rendimento igual a 1.
De forma geral, o rendimento (η) de uma máquina térmica equivale à razão entre o trabalho útil (τ) gerado e o calor (Q₁) recebido da fonte quente:

Substituindo o trabalho da fórmula acima pela expressão dada anteriormente (τ = |Q₁| - |Q₂|), encontramos uma segunda fórmula para o cálculo do rendimento:
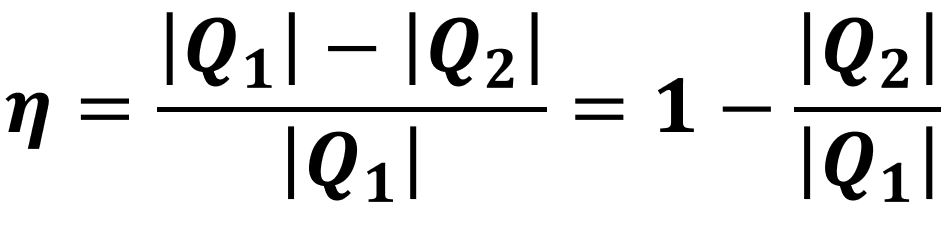
Ciclo de Carnot
Na prática, o rendimento de uma máquina térmica pode depender de diversas variáveis. Podemos citar, dentre elas, a tecnologia utilizada em sua construção e o fluido que opera em seu interior. Além disso temos, principalmente, as transformações termodinâmicas pelas quais esse fluido passa e a temperatura em que se encontram as fontes fria e quente.
Em 1824, o jovem engenheiro francês Nicolas Léonard Sadi Carnot (1796-1832) propôs uma máquina térmica teórica ideal, ou seja, uma máquina que teria o maior rendimento possível, dadas as temperaturas das fontes.
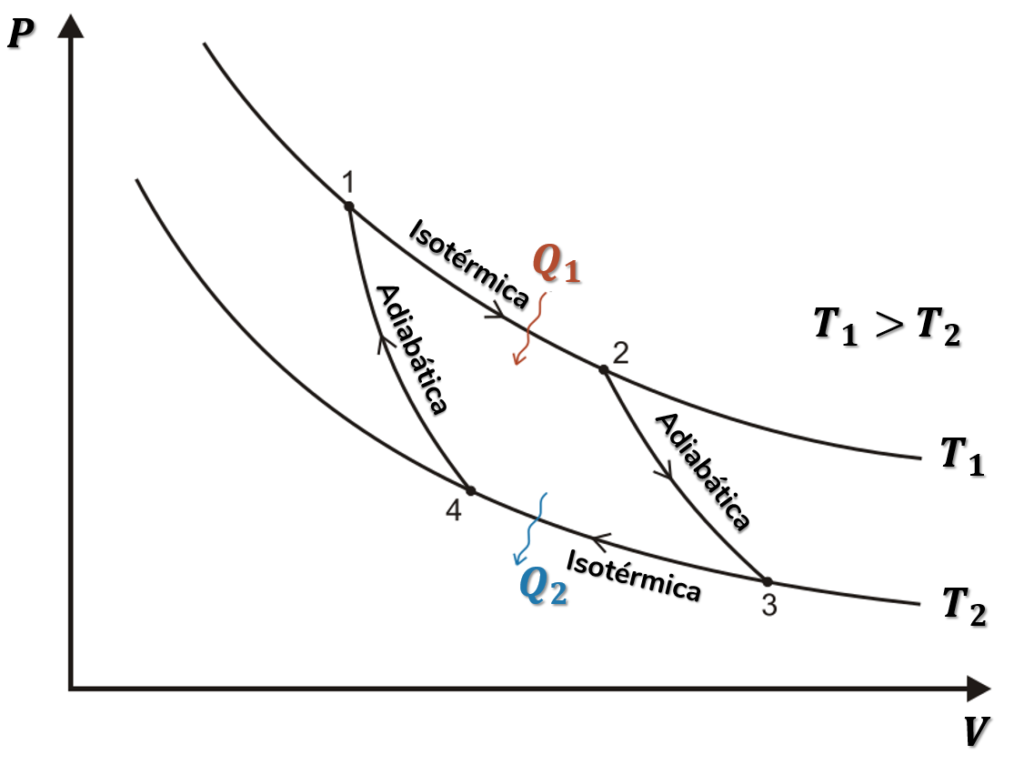
Para tal, essa máquina deveria seguir um ciclo termodinâmico específico: o chamado ciclo de Carnot. Para um gás ideal, o ciclo de Carnot é composto de duas transformações isotérmicas e duas transformações adiabáticas. Observe na imagem abaixo a representação desse ciclo em um gráfico de pressão (P) por volume (V):
Um fato interessante é que, nesse ciclo, os calores trocados com as fontes e as temperaturas absolutas (temperaturas medidas em kelvin) dessas fontes possuem uma relação de proporcionalidade:
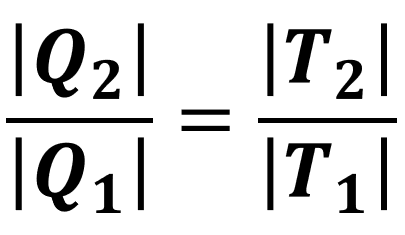
Dessa forma, podemos calcular o rendimento de uma máquina que segue o ciclo de Carnot sabendo apenas as temperaturas de suas fontes:
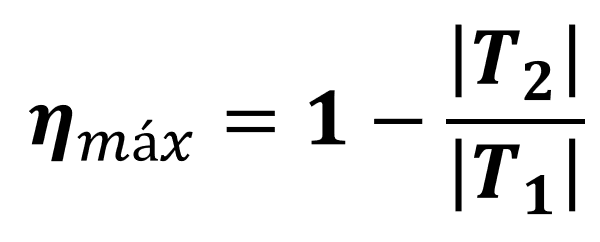
Esse rendimento é conhecido como o rendimento máximo de uma máquina térmica, já que:
"Nenhuma máquina operando entre duas temperaturas fixadas pode ter rendimento maior do que uma máquina ideal de Carnot que opera entre essas mesmas temperaturas."
Esse é o primeiro postulado de Carnot.
Note também que esse rendimento máximo nunca atinge o valor 1, ou seja, ele não viola a segunda lei da termodinâmica. Para tal, a temperatura da fonte fria teria que ser 0 K, ou seja, zero absoluto. Isso é impossível, pois nenhuma sistema físico pode de fato atingir tal temperatura.
Outro fato curioso é enunciado pelo segundo postulado de Carnot:
"Operando entre duas temperaturas fixas, o rendimento é o mesmo para uma máquina ideal de Carnot, independentemente do fluido operante."
Refrigeradores e a segunda lei da termodinâmica
Vamos estudar agora um segundo enunciado da segunda lei da termodinâmica, o enunciado de Clausius:
"É impossível que uma máquina, sem a ajuda de um agente externo, consiga conduzir calor de um sistema para outro que esteja a uma temperatura maior."
Na verdade, essa é a apenas a formalização de algo que podemos perceber em nosso cotidiano: calor nunca irá fluir espontaneamente de um corpo para outro mais quente. Por exemplo, se você largar uma xícara de café quente sobre a mesa, o calor sempre vai fluir do café (temperatura maior) para o ambiente (temperatura menor), e nunca o contrário.
Tá, mas então como as geladeiras e os ar-condicionados funcionam? Um ar-condicionado, por exemplo, remove calor do interior de um cômodo (temperatura menor) e libera calor no exterior (temperatura maior). Isso tudo não viola a segunda lei da termodinâmica? Não, pois esse processo não é espontâneo, e sim forçado!
Na física, chamamos de refrigerador uma máquina capaz de transferir calor de uma região mais fria para uma região mais quente. Para forçar essa transferência, é necessária a realização de um trabalho por parte da máquina. É por essa razão que os ar-condicionados e geladeiras precisam estar conectados na tomada: eles utilizam energia elétrica para realizar esse trabalho.
Conservação da Energia em Refrigeradores
De forma análoga ao que foi feito para as máquinas térmicas, podemos analisar a conservação de energia em um refrigerador:
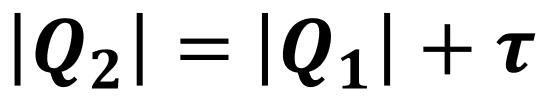
Note que, o calor (Q₂) rejeitado na fonte quente é equivalente à soma do calor (Q₁) retirado da fonte fria e do trabalho (τ) realizado pelo refrigerador, ou seja, Q₂ será sempre maior do que Q₁.
Sendo assim, se você deixar a porta da geladeira aberta, a temperatura da cozinha aumentará ao invés de diminuir. Isso acontece porque mais calor está sendo introduzido no ambiente pela parte posterior do equipamento (fonte quente) do que sendo removido pela parte da frente (fonte fria).
Observe no esquema abaixo um resumo do funcionamento de qualquer refrigerador:
Eficiência dos Refrigeradores
Semelhante ao rendimento das máquinas térmicas, para os refrigeradores, temos um índice chamado de eficiência (ε). Basicamente, quanto maior é a eficiência de um refrigerador, menos trabalho ele precisa realizar para remover uma determinada quantidade de calor da fonte fria.
Para encontrar o valor exato dessa eficiência (ε), basta calcular a razão entre o calor (Q₁) retirado da fonte fria e o trabalho (τ) realizado pelo refrigerador:
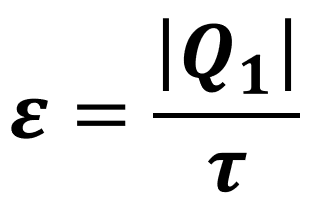
Substituindo o trabalho da fórmula acima por uma adaptação da expressão dada anteriormente (τ = |Q₂| - |Q₁|), encontramos uma segunda fórmula para o cálculo da eficiência:
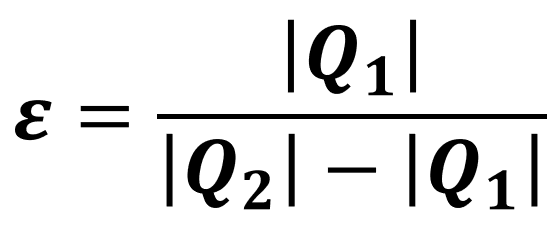
Entropia e a segunda lei da termodinâmica
Por fim, estudaremos uma terceira forma de enunciar a segunda lei da termodinâmica: através da entropia. A entropia (S) é a medida da "desordem" de um sistema. Quanto maior é a desordem, maior é a entropia.
A física nos diz que, com o passar do tempo, a desordem de um sistema fechado (que permite trocas de energia, mas não de matéria) tende sempre a aumentar e nunca a diminuir. Ou seja, a entropia de um sistema fechado também tende sempre a aumentar. Dessa forma, podemos concluir que, como um todo, a entropia do universo vem aumentando ao longo do tempo. Quer saber mais sobre o assunto? Temos um post completo sobre entropia.
Tá, mas qual é a relação da entropia com o que vimos sobre a segunda lei da termodinâmica?
Bom, sabemos que nenhum dispositivo pode transformar em trabalho útil toda a energia térmica que recebe na forma de calor. Sendo assim, podemos inferir que parte dessa energia não é "aproveitável".
E, nesse contexto, também podemos definir a entropia como uma grandeza que mensura essa parcela de energia. Energia essa que não é aproveitável para gerar trabalho.
Em geral, não nos preocupamos com o valor exato da entropia de um sistema, mas sim com a variação (ΔS) dela ao longo de um processo termodinâmico. Podemos calcular essa variação através da razão entre o calor trocado pelo sistema (Q) e a sua temperatura absoluta (T, em kelvins):
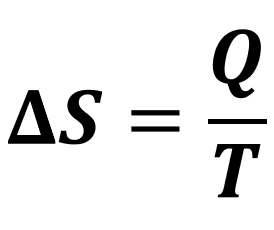
Agora que você já sabe tudo sobre a segunda lei da termodinâmica, em todas as suas formas, é hora de praticar. Bons estudos!
📖 Quer saber mais sobre esse e outros conteúdos, além de ter acesso às melhores videoaulas para se preparar para os vestibulares e Enem? A plataforma Aprova Total tem tudo isso e muito mais!




