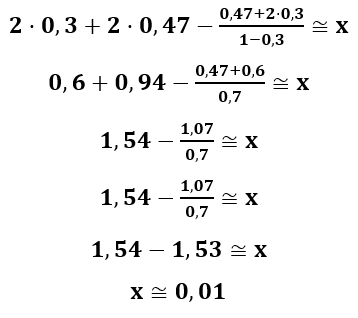Logaritmo: Conceito, Propriedades e Exemplos

O logaritmo é um dos conteúdos abordados dentro do universo matemático. Ele é estudado, cotidianamente, por diversos temas em análise estatística, curvas de crescimento/decrescimento de uma população de dados e entre outros. Além disso, esse conteúdo sempre está presente nos assuntos abordados pelo ENEM.

Dessa forma, este artigo foi desenvolvido para você entender ou revisar o conceito e as propriedades do logaritmo. Todavia, para entender logaritmo, é necessário o mínimo de conhecimento sobre potenciação e função exponencial. Portanto, iniciaremos com uma breve revisão sobre esses temas para você.

Potenciação

A potenciação é um recurso matemático essencial para o estudo do logaritmo, pois ela é a base para a construção deste.

Primeiramente, a potenciação nada mais do que um processo ou operação matemática que resume um conjunto de multiplicações de mesmo número x vezes. Exibindo graficamente, temos:

Dizemos que a é a base da potência e x o expoente e, também, que a está elevado a x.

Exemplo:

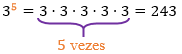
Em casos menos intuitivos, como por exemplo, 3^-5, é estranho pensar que essa potência seria o número 3, multiplicado por ele mesmo, por -5 vezes. Porém, esta situação pode ser explicada por definição de um elemento inverso, o que não nos interessa nesse artigo. Dessa forma, basta saber que , ou seja, o exemplo acima seria:

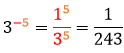
Além do expoente negativo, o expoente de uma potência pode ser um número fracionário. Nesse caso, então, teremos que conhecer radiciação. Entretanto, para não alongar o assunto, dizemos que uma potência , ou seja, pelo exemplo:

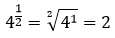
Para finalizar, por definição, se um número é elevado ao expoente igual a 0, então esse número é igual a 1, ou seja, a⁰ = 1.

Agora que você já está ligado sobre a potenciação podemos partir para a função exponencial!

Função Exponencial

É importantíssimo que você saiba sobre função exponencial para que entenda as condições de existências do logaritmo. Dessa maneira, a função exponencial é a função cuja lei de formação é do tipo: f(x) = a^x, ou seja, é uma potência em que o resultado depende do expoente.

Além disso, essa função é bem definida para valores em que a, ou seja, a base da potência, for maior que 0 e diferente de 1, isto é, f(x) = a^x, a > 0 e a ≠ 1. Isso ocorre, pois se a função exponencial possui como base da potência os valores 0, 1 ou qualquer outro valor menor que 0, ela perde a característica de exponencial, gradativo, etc.

Portanto, se a base de uma potenciação é maior que 0 e diferente de 1, então, para qualquer valor de seu expoente o resultado será sempre maior que 0, portanto f(x) > 0.

Ademais, ao analisar a lei de formação da função exponencial e esboçar o seu gráfico, encontramos uma figura semelhante a essa:

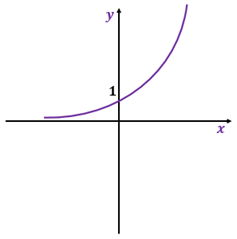
Agora que você já viu as condições de existência de uma função exponencial e a sua lei de formação básica, podemos introduzir o logaritmo.

Logaritmo

Anteriormente, falamos sobre potências e função exponencial, esses assuntos foram necessários para a introdução do logaritmo pelo motivo de que este é definido como a função inversa da função exponencial. Entretanto, para entender o porquê dessa afirmação, é necessário que você saiba como é um logaritmo.

O logaritmo, assim como a potência, é uma operação matemática. Entretanto, este, apresenta algumas peculiaridades e uma pequena diferença em relação à potenciação. Enquanto na potenciação, uma base a, elevada a um expoente x, resulta em um número b. No logaritmo, por outro lado, o resultado desse número b, com a mesma base a, deve ser igual ao expoente x. Isto é, se a^x = b, então, log_a b = x. Acompanhe a imagem abaixo:

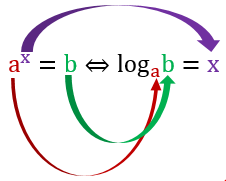
Por definição, ‘log’ é a identificação de logaritmo e, com isso, dizemos que a é a base, b é o logaritmando e, por fim, x é o logaritmo.

Exemplo:

3² = 9, então, log₃ 9 = 2

Condição de Existência

Todavia, como falado anteriormente, existem condições de existências em um logaritmo, pois ele é a função inversa da função exponencial e, consequentemente, o logaritmo possui as mesmas condições de existência que a função exponencial pelos mesmos motivos explicados.

Teoricamente falando, dados:

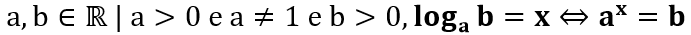
Em linguagem descritiva, dados dois números, a e b, que pertencem ao conjunto dos números reais. Além disso, a deve ser maior que 0 e diferente de 1, mas também, por consequência, b será maior que 0. Portanto, o logaritmo de b na base a é igual a x se, e somente se, a elevado a x é igual a b.

Em resumo, para um logaritmo de base a e logaritmando b, as condições de existência para esse logaritmo são: a > 0, a ≠ 1 e b > 1.

Logaritmo: Função Inversa da Função Exponencial

Por conta da definição de que um logaritmo é a função inversa da função exponencial, os gráficos dessas respectivas funções devem ser simétricos. Portanto, os gráficos de f(x) = log_a x e f(x) = a^x se assemelham a seguinte simetria:

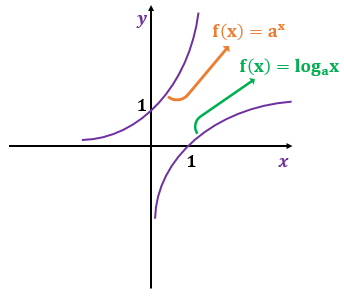
Sabendo a definição dos logaritmos e sua condição de existência, podemos descobrir alguns casos particulares no logaritmo.

Casos Particulares

Ao realizar inferências, descobrimos alguns casos particulares em logaritmos. Veja abaixo alguns.

• Se o logaritmando de qualquer logaritmo é igual a um 1, então, não importa qual base for, o resultado é igual a 0.

log_a 1 = 0, pois, a⁰ = 1

• Caso o logaritmando tenha o mesmo valor da base, então, o logaritmo deve ser igual a 1.

log_a a = 1, pois, a¹ = a

• Se, em alguma circunstância, a base de um logaritmo é um número a e o logaritmando for a^b, então, o resultado dessa operação é b.

log_a a^b = b, pois, a^b = a^b

• Quando dois logaritmos possuírem a mesma base e eles estão em uma igualdade, é afirmativo que seus logaritmandos são iguais também.

log_a b = log_a c, então, b = c

Exemplo:

log₂ x = log₂ 4, então, x = 4

• Caso a potência de um número a for um logaritmo de base a e logaritmando b qualquer, então, o resultado dessa potência será o número b.

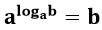
Exemplo:

2^log­₂⁴ = 4, pois, log₂ 4 = 2, então, 2² = 4

• Se um logaritmo não apresentar base, está implícito que a base dele é 10. Para essa condição, o chamamos de logaritmo decimal.

log 100 = 2, pois, log 100 = log₁₀ 100 e, também, 10²= 100

Propriedades do Logaritmo

Chegou a hora de você conhecer as propriedades dos logaritmos, elas são muito úteis para a resolução exercícios de ENEM e vestibulares. Portanto, veja elas a seguir:

Adição de Logaritmos de mesma Base

Nessa primeira propriedade, dado a soma de dois logaritmos de mesma base a, dizemos que essa soma é igual ao logaritmo do produto dos dois logaritmandos com a mesma base a. Portanto:

log­­_a b + log_a c = log_a (b ⋅ c)

Essa propriedade é conhecida, também, por logaritmo de um produto.

Subtração de Logaritmos de mesma Base

Caso tenha uma diferença de dois logaritmos de mesma base a, dizemos que essa diferença é igual ao logaritmo da razão entre os dois logaritmandos com a mesma base a. Representando por meio dos logaritmos:

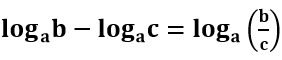
Pode-se dizer que essa propriedade tem o nome, também, de logaritmo do quociente.

Produto de um Logaritmo e um Número

Se tivermos um número n multiplicando um logaritmo qualquer de logaritmando b e base a, então, é possível afirmar que essa multiplicação é igual ao logaritmo de b^­ elevado a n e mesma base a. Em outros termos:

n ⋅ log_a b = log_a bⁿ

Essa propriedade, também, é denominada por logaritmo de uma potência.

OBS: Perceba que n pode ser um número fracionário e, portanto, quando uma base se eleva a um expoente fracionário, possuímos uma raiz de índice n.

Exemplo:

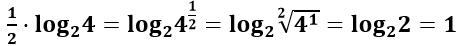
Base Elevado a um Expoente

Se a base a de um logaritmo estiver elevada a n, então, esse logaritmo é igual ao produto do inverso de n pelo mesmo logaritmo de base a. Ou seja:

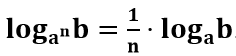
Mudança de Base de Logaritmo

Caso seja necessário a mudança de base de um logaritmo de base a e logaritmando b, basta escolher uma nova base n. Após isso, a razão de um logaritmo, de base n e logaritmando b, por um outro, de mesma base n e logaritmando a, equivalem ao logaritmo inicial. Isto é:

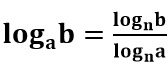
Como Resolver Logaritmo?

Sabendo o que é logaritmo, seus casos particulares e suas propriedades, resta saber como se calcula ele. Para isso, vamos resolver o exemplo abaixo:

log₃ 243

Primeiramente, desejamos saber o valor desse logaritmo. Dessa forma, podemos igualar ele a um número x que será nossa resposta:

log₃ 243 = x

A partir disso, vem a parte principal para resolução do logaritmo: aplicar a definição de logaritmo, ou seja, saber que um logaritmo de uma base a e logaritmando b é igual a x, se, e somente se, a elevado a x é igual a b. Dessa maneira, temos:

log₃ 243 = x ⇔ 3^x = 243.

Nessa parte você chegou a uma equação exponencial. Para resolve-la, devemos decompor, em fatores primos, o número 243 até encontrarmos a mesma base da potência (3), se possível.

OBS: Se você não sabe como decompor um número em fatores primos, recomendamos a leitura do nosso post sobre MMC, no qual explicamos passo a passo como realizar essa decomposição.

Seguindo com a decomposição de 243, encontramos a potência que equivale a ele, isto é, 3⁵. Sendo assim, podemos igualar a nossa equação exponencial 3^x com 3⁵:

3^x = 3⁵

Como as bases estão iguais, portanto, dizemos que os expoentes também devem ser iguais e, por isso:

x = 5

Exemplos de Logaritmos

Agora que você já sabe resolver logaritmos, vamos encontrar os valores de x para alguns simples exemplos que podem aparecer em seus vestibulares.

Exemplo 1

log₄ 8 + log₄ 32 – 2 ⋅ log₄ 2 = x

Ao analisar a expressão, podemos verificar várias propriedades dos logaritmos: adição e subtração de logaritmos de mesma base e produto de um número com um logaritmo. Dessa forma, vamos aplica-las na expressão:

log₄ 8 + log₄ 32 – 2 ⋅ log₄ 2 = x

(log₄ 8 + log₄ 32) – (2 ⋅ log₄ 2) = x

Usamos, nos primeiros parênteses, a propriedade da adição de logaritmos de mesma base. Por outro lado, nos segundos parênteses, usamos a propriedade do produto de um logaritmo por um número qualquer:

[log₄ (8 ⋅ 32)] – (log₄ 2²) = x

log₄ 256 – log₄ 4 = x

Nesse momento, podemos aplicar a propriedade de subtração de logaritmos de mesma bases, ou seja:

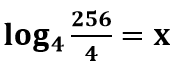
log₄ 64 = x

Agora que reduzimos a expressão para um único logaritmo, podemos aplicar a definição e encontrar o valor desse logaritmo:

log₄ 64 = x, então, 4^x = 64

Sabendo que 64 é igual a 4³, então:

4^x = 4³

Finalmente, encontramos que a expressão inteira equivale a x = 3.

Exemplo 2

Dados (log 2 ≅ 0.3 e log 3 ≅ 0.47):

log 15 = x

Analisando esse logaritmo, podemos ver que ele é de base 10, pois não temos nenhuma base exibida. Além disso, perceba que foram dados valores para alguns logaritmos decimais (log 2 ≅ 0.3 e log 3 ≅ 0.47). Dessa forma, é possível aplica-los caso necessário, portanto, observando que 15 é igual a 3 ⋅ 5, ou seja:

log 3 ⋅ 5 = x

Sendo assim, perceba, ainda, que 5 equivale a 10 sobre 2, portanto:

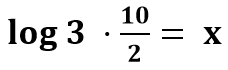
Por consequência, note que podemos aplicar as propriedades dos logaritmos e separarmos os três valores:

log 3 + log 10 – log 2 = x

Por fim, basta substituir os valores de log 2 e de log 3 e notar que log 10 = 1, pois 10¹ = 10, dessa forma:

0,47 + 1 - 0,3 ≅ x

x ≅ 1,17

Exemplo 3

Dados (log 2 ≅ 0.3 e log 3 ≅ 0.47):

log 4 + log 9 – log₅ 12 = x

Nesse último exemplo, temos uma expressão diferente das outras, pois, anteriormente, todas tinham a mesma base. Por outro lado, nesse exemplo, temos três logaritmos e duas bases distintas. Dessa maneira, para facilitar, podemos aplicar a propriedade de mudança de logaritmo.

OBS: Perceba que a base 10 é a melhor base para usar nesse exemplo, pois já temos valores dados (log 2 e log 3) e, se mudarmos os logaritmos de base 10 para base 5, não teremos vantagens. Portanto, aplicamos a mudança de log no logaritmo de base 5 para base 10:

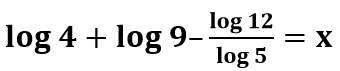
Agora, a forma mais simples de encontrar o valor de x é aplicando as propriedades do logaritmo e encontrando valores que possuímos (log 2, log 3 e os logaritmos das potências de 10). Sendo assim, note que 4 é a mesma coisa que 2² e que 9 é igual a 3², por consequência:

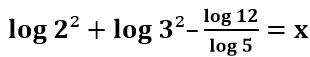
Ademais, podemos fatorar o número 12 por números primos, ou seja, 3 ⋅ 2² e, também, é afirmativo que 5 é a 10 dividido por 2.

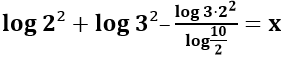
Nesse instante, todos os valores da expressão são dados, portanto, basta que aplicamos as propriedades para separarmos um logaritmando para cada logaritmo:

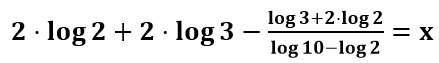
Finalmente, resta substituir os valores em cada logaritmo e determinar o valor de x: