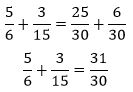Descubra o que é MMC e como resolver

Com a proximidade do Enem e vestibulares, é hora de fazer uma revisão dos principais tópicos de cada disciplina! Em Matemática, neste post, vamos falar sobre Mínimo Múltiplo Comum (MMC). Para o MMC ser compreendido da melhor maneira, primeiro é preciso entender alguns conceitos anteriores. Então, vamos começar:

Múltiplos

Entender múltiplos é o primeiro passo para começar a compreender MMC. Os múltiplos de um número são todos aqueles que resultam da multiplicação desse número por outro.

Por exemplo: os múltiplos de 5 são todos os números que resultam da multiplicação de 5 por outro número:

5 × 0 = 0 | 5 × 1 = 5 | 5 × 2 = 10

Ou seja, os múltiplos de 5 são os elementos do conjunto M(5): {0, 5, 10, 15, 20, 25, ...}

Múltiplos em Comum

Os múltiplos em comum de dois ou mais números são os números que são múltiplos de todos os números envolvidos. Dessa maneira, usaremos, como exemplo, os números 2 e 3.

            Os múltiplos desses dois números são:

M(2): {0, 2, 4, 6, 8, 10, 12, 14, 16, 18...}

M(3): {0, 3, 6, 9, 12, 15, 18, 21, 24, 27...}

Note que os múltiplos em comum são os múltiplos que aparecem tanto em um quanto no outro: 

M(2): {0, 2, 4, 6, 8, 10, 12, 14, 16, 18, ..., 24...}

M(3): {0, 3, 6, 9, 12, 15, 18, 21, 24, 27...}

Portanto, os múltiplos, em comum, de 2 e 3 são 0, 6, 12, 18...

Mínimo Múltiplo Comum (MMC)

Se você chegou até aqui você está pronto para entender o que é o m.m.c., retomando o exemplo anterior, os múltiplos em comum de 2 e 3 são os elementos do conjunto {0, 6, 12, 18, ...}. Além disso, como você deve ter imaginado, o mínimo múltiplo comum entre eles deve ser o menor desses números e, pela lógica, seria o 0. Mas, relembrando o início da leitura, o m.m.c. é o menor múltiplo excluindo o zero, pois o zero é múltiplo de todos os números, portanto ele deve ser desconsiderado.

Sendo assim, m.m.c.(2, 3) = 6.

Decomposição dos Números em Fatores Primos

Para calcular o m.m.c. de um número é importante entendermos o processo de decomposição dos números em produto de fatores primos. Sendo assim, um número inteiro (Veja o nosso post sobre números inteiros) positivo, maior que um pode ser decomposto em um produto de fatores primos que são divisores desse número. Então, usando o número 210 como exemplo, devemos dividir esse número pelos seus divisores que são números primos. Como o número é par, ele é divisível pelo número primo 2 e, portanto:

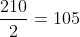
Observe que o resultado da divisão é divisível por 3, dessa forma:

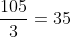
Da mesma maneira, o resultado é divisível por outro primo, o número 5:

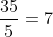
Finalmente chegamos ao último número primo que é divisível por esse resultado, ou seja, o número 7:

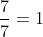
Perceba que a multiplicação de todos os números primos que estão no denominador resultam no número original, ou seja:

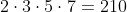
Dessa forma, a decomposição do número 210 em fatores primos pode ser representada por .

Cálculo de MMC

Anteriormente, você viu uma maneira de calcular o MMC de dois números através do método da comparação. Porém, se os números forem maiores o cálculo fica mais desgastante e, por isso, há outros meios de calcular o m.m.c. entre números. Os mais usados são o método da fatoração e o da decomposição simultânea.

Fatoração

Para calcular o m.m.c. de 4, 9 e 15, deve-se, primeiramente, decompor os números:

4 = 2 × 2

9 = 3 × 3

15 = 3 × 5

Para calcular o m.m.c., deve-se multiplicar os fatores primos comuns e não comuns dos números. Observe que os números comuns estão na mesma cor, portanto, o resultado é 2 × 2 × 3 × 3 × 5 = 180. Logo, m.m.c. (4, 9, 15) = 180.

Quer saber como a Matemática é cobrada no ENEM? Então confira o nosso post sobre o assunto!

Decomposição Simultânea

Para determinar o menor múltiplo comum de dois ou mais números por esse método, deve-se fatorar todos os números, ou seja, transformá-los em produtos de números primos em um dispositivo semelhante ao abaixo:

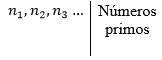
Utilizaremos como exemplo, os mesmos números do exemplo anterior. Após colocar os números no dispositivo, deve-se notar quais números primos são divisores de quaisquer um destes números. Se você perceber, os números 2, 3 e 5 são os únicos divisores primos dos três números (não necessariamente simultaneamente) e, dessa forma, deve-se colocar o menor número primo no dispositivo e dividir os múltiplos desse primo.

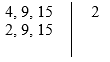
Note que agora temos números novos na segunda linha e, portanto, deve-se continuar o processo.

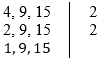
Como visto anteriormente, o número primo ‘2’ não é divisor de nenhum dos novos números, então, o próximo primo deve ser colocado no dispositivo e continuar o processo até sobrem apenas o número 1 para cada um dos números.

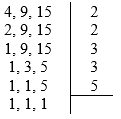
O m.m.c. entre os números 4, 9 e 15 é o produto entre os primos que apareceram ao lado direito do dispositivo, logo:

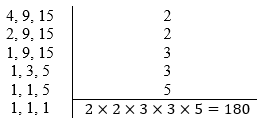
Então, m.m.c. (4, 9, 15) = 180.

Propriedades do MMC

Existem algumas propriedades de m.m.c. que facilitam o seu cálculo. Portanto, veja-as a seguir:

• Suponha dois ou mais números, se um deles for múltiplo dos demais, então este número é o m.m.c. entre os números de interesse.
  Exemplo: 4, 5 e 20. O número 20 é múltiplo de 4 e 5, portanto, ele é o m.m.c. dos três números.

• O m.m.c. de dois ou mais números que são primos entre si é o produto deles.
  Exemplo: 3, 5, e 8. Como todos são primos entre si, o m.m.c. deles é .

  Observação: dois números são primos entre si quando o maior número que divide os dois ao mesmo tempo é o 1.

Aplicações do MMC na Matemática

Na área da matemática, o m.m.c. é muito usado para adições e subtrações de frações com denominadores distintos, tome como exemplo, a soma de frações a seguir:

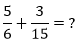
Para resolve-la, é necessário sabermos o m.m.c. dos denominadores, que é m.m.c. (6, 15) = 30.

Sabendo que qualquer número dividido por ele mesmo resulta em 1, ou seja,   e, além disso, qualquer número multiplicado por 1 resulta nele mesmo, isto é, . Por consequência, ao multiplicarmos a soma das frações por , a fração não será alterada. Acompanhe abaixo a resolução:

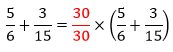
Dessa maneira, ao aplicar a propriedade distributiva:

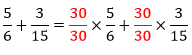
Perceba, agora, que os denominadores das frações (6 e 15) podem ser simplificados por 30 pois estão em multiplicação de frações, sendo assim:

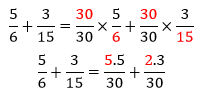
Note que os denominadores agora são iguais e representam o m.m.c. dos denominadores antigos, portanto, é possível calcularmos a soma das frações: