Empuxo: o que é, como funciona, fórmulas e exercícios

Você sabe por que um navio transatlântico flutua na água, mesmo sendo tão pesado, enquanto alguns objetos leves, como um parafuso, afundam? Para entender isso, você precisa conhecer o conceito de empuxo, uma força que está sendo exercida sobre você agora mesmo e você nem se dá conta!

O que é empuxo (Princípio de Arquimedes)?

Empuxo é uma força exercida por fluidos, ou seja, por líquidos e gases, sobre corpos que neles estejam imersos. Essa força tem a direção vertical e sentido de baixo para cima. O módulo do empuxo corresponde ao módulo do peso do fluido deslocado pelo corpo.

Essas características do empuxo são descritas pelo princípio de Arquimedes, enunciado no século III a.C. por Arquimedes de Siracusa.

Imagine uma esfera de 1 m³ de volume, como na ilustração abaixo. Se essa esfera for totalmente submersa na água dentro de um recipiente, ela ocupará o volume de uma região onde antes havia água, ou seja, a esfera deslocou uma porção de 1 m³ de água. Afinal, o mesmo 1 m³ da esfera está numa região antes ocupada pela porção de água deslocada.

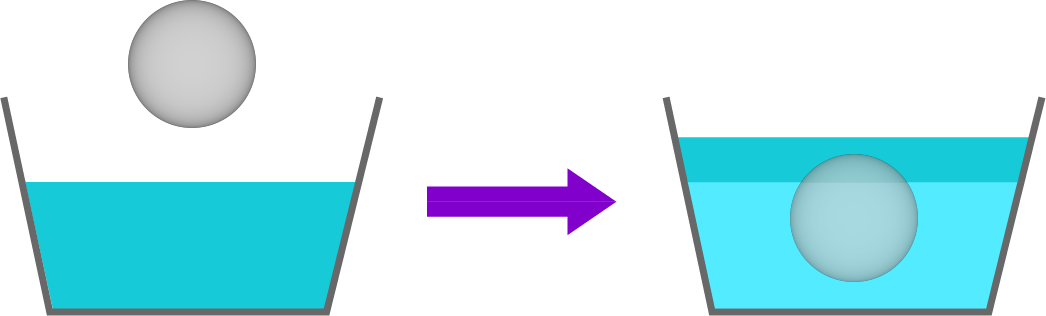
Na imagem, essa porção deslocada de água está representada pela cor mais escura no desenho da direita. O volume dessa porção é igual ao volume da esfera. Pelo princípio de Arquimedes, o módulo do empuxo exercido sobre a esfera é igual ao módulo do peso da porção deslocada de água.

É importante notar que o volume de água deslocada é igual ao volume da esfera porque ela está totalmente submersa. Caso somente uma parte da esfera estivesse submersa, ela deslocaria uma porção de água cujo volume seria igual apenas ao dessa parte submersa.

Como o empuxo acontece?

Afinal, por que os fluidos exercem empuxo? E por que ele aponta de baixo para cima? Primeiramente, vamos nos lembrar do seguinte: quanto maior for a coluna de fluido acima de um corpo, maior será a pressão hidrostática sobre ele.

Na figura abaixo, temos diversas forças aplicadas pela água sobre uma esfera nela submersa. Veja que as forças são mais intensas na parte inferior da esfera, pois a pressão hidrostática é maior embaixo do que em cima.

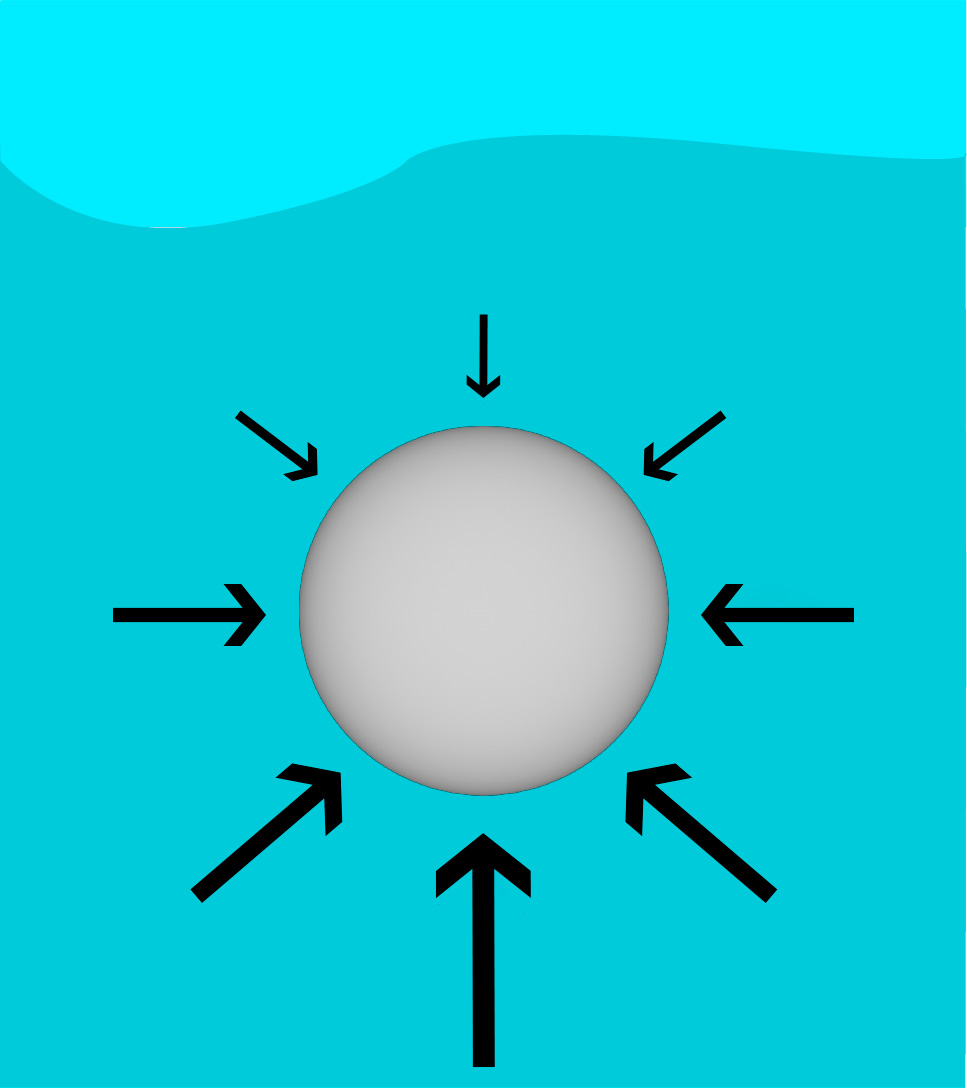
Nas laterais, as forças se equilibram porque, para cada força lateral no lado esquerdo, há uma lateral no lado direito, a uma mesma altura, que tem mesmo módulo, mesma direção e sentido contrário.

Dessa forma, se fizermos somas vetoriais de todas as forças que a água exerce sobre a esfera, as componentes horizontais se anulam, restando uma componente vertical para baixo e outra para cima:

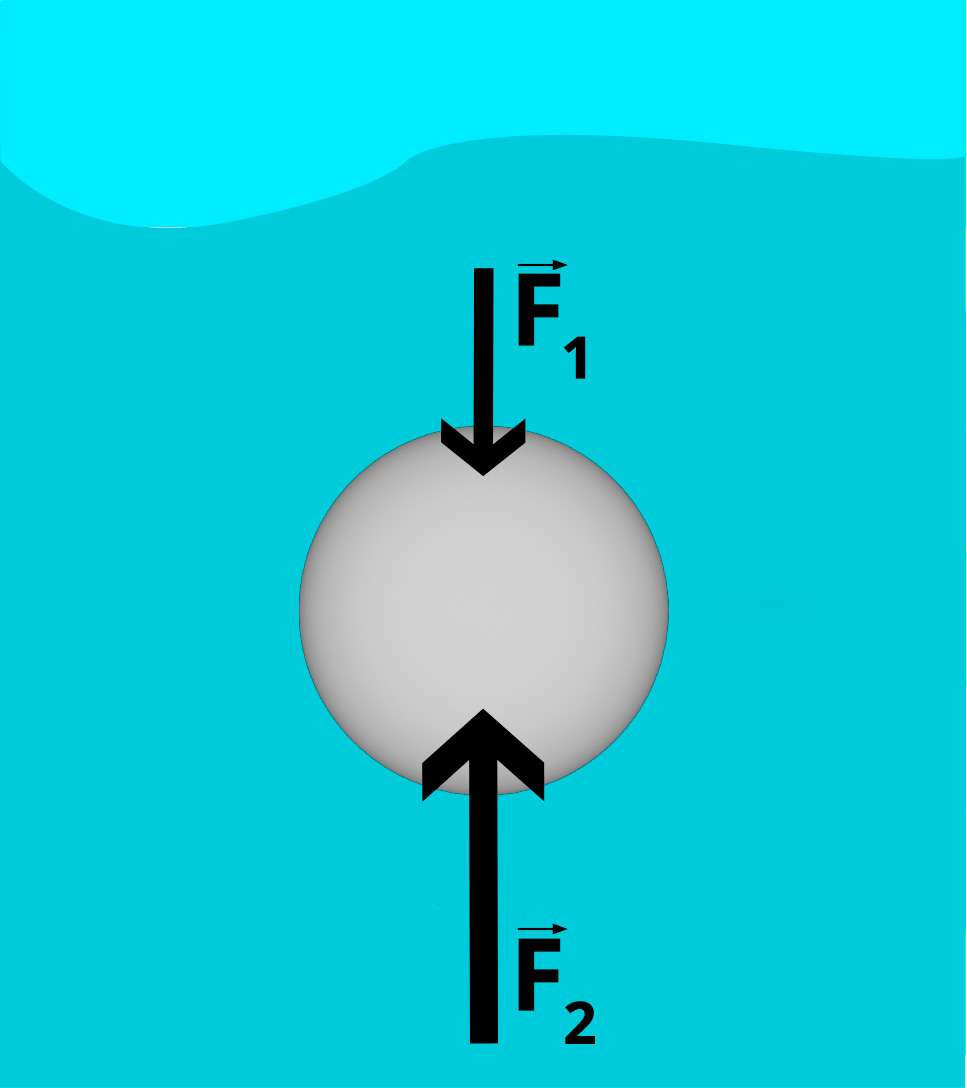
Como a força de módulo F₂ é mais intensa do que a força de módulo F₁, a força resultante aponta de baixo para cima e seu módulo é dado por F₂ - F₁. Essa força resultante exercida pela água é o empuxo.

Conceitos importantes para entender o empuxo

Antes de aprender as fórmulas que usamos para calcular empuxo, é importante relembrar os conceitos de densidade e de peso.

Densidade

Densidade é a razão entre a massa (m) de um corpo e o seu volume (V). Portanto, a fórmula para calcular a densidade (d) é

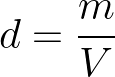
Sendo assim, para um mesmo volume, quanto maior for a massa do corpo, maior será a sua densidade, como podemos ver na imagem abaixo:

O volume dos dois blocos é o mesmo, mas, para esse mesmo volume, o bloco da direita tem mais massa concentrada, logo, sua densidade é maior.

Existe ainda uma grandeza chamada massa específica (ρ), que também é a razão entre massa e volume, mas, diferente da densidade, a massa específica considera somente a massa de uma substância e o volume ocupado por ela.

Por exemplo: uma moeda feita inteiramente de aço maciço tem a mesma massa específica que um balde feito do mesmo tipo de aço, já que a massa específica considera apenas o volume ocupado pela substância. No entanto, o balde é menos denso, pois sua massa ocupa um volume muito maior, considerando o corpo como um todo.

Peso

Sabemos, dos estudos de Dinâmica, que o módulo da força peso de um corpo é dado por P = m · g, sendo m a sua massa e g a aceleração gravitacional.

Podemos usar essa fórmula para calcular o peso de qualquer corpo, incluindo uma porção de fluido. Entretanto, as questões de empuxo costumam trazer a fórmula do peso de outra forma: reescrevendo a massa usando a densidade e o volume do fluido.

Como d = m/V, podemos isolar m e escrever m = d · V. Substituindo m por d · V, podemos obter uma nova cara para a fórmula do peso de um fluido:

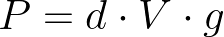
Fórmulas do empuxo

Pelo princípio de Arquimedes, sabemos que o empuxo sobre um corpo imerso em um fluido é igual ao peso do fluido deslocado por esse corpo. Como P = m · g, podemos obter uma fórmula para o empuxo:

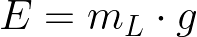
Em que m_L é a massa da porção deslocada de líquido (mas lembre que isso vale para gases também). Usando a outra fórmula que encontramos para o peso, podemos reescrever essa fórmula:

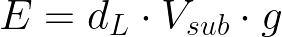
Sendo d_L, a densidade do líquido; V_sub, o volume submerso do corpo (que, como aprendemos, é igual ao volume de líquido deslocado); e g, novamente, a aceleração gravitacional. Se você precisar de uma fórmula do empuxo, essa é a ideal!

Contudo, em muitas questões, você nem vai precisar utilizá-la, pois é comum que elas exijam apenas cálculos a partir de diagramas de forças, relacionando o empuxo com outras forças, sem necessariamente aplicar a sua fórmula.

👉 Leia também

Fórmulas de Física que você precisa saber para o Enem

Hidrodinâmica: veja princípios, fórmulas e exercícios

Por que um corpo afunda ou flutua? Casos de flutuação

O que determina se um corpo afunda ou flutua não é apenas o seu peso, mas a forma como o peso se compara com o empuxo. Para isso, o volume do corpo é extremamente importante. Além disso, podemos comparar a densidade de um corpo com a densidade do líquido onde ele está submerso para saber se ele afunda ou flutua. Temos três casos de flutuação:

• O corpo flutua no líquido: nesse caso, a densidade do corpo é menor do que a densidade do líquido. Enquanto o corpo, inicialmente submerso, está subindo, o empuxo é maior do que o peso.
• O corpo afunda no líquido: isso acontece porque a densidade do corpo é maior do que a densidade do líquido. O corpo afunda porque o peso é maior do que o empuxo.
• O corpo não flutua nem afunda no líquido: ocorre quando o corpo e o líquido têm mesma densidade. O peso e o empuxo são iguais em módulo.

O que faz um corpo afundar ou flutuar?

Imagine o seguinte exemplo: uma bola de praia e uma bola maciça de canhão, ambas de mesmo volume, são seguradas dentro da água.

Se soltarmos as bolas, o que vai acontecer é intuitivo: a bola de canhão vai afundar, enquanto a bola de praia vai subir. Afinal, a bola de praia está cheia de ar, enquanto a bola de canhão é maciça, muito mais densa do que a de praia.

Apesar de suas densidades serem diferentes, o empuxo sobre ambas as bolas é igual! Lembra que o empuxo é igual, em módulo, ao peso do fluido deslocado? 😉 Como as duas bolas têm mesmo volume, ambas deslocam a mesma quantidade de água!

É aqui que se encontra a diferença: para volumes iguais, o corpo que tiver mais massa será mais denso (pois d = m/V). Por ser mais densa do que a água, a bola de canhão afunda. Em contrapartida, por ser menos densa do que a água, a bola de praia flutua.

Como o peso se relaciona com o empuxo?

Vamos considerar o mesmo exemplo anterior. Vimos que, apesar das diferenças de massa e de densidade, ambas as bolas têm mesmo volume e, portanto, sofrem ação de empuxos de módulos iguais.

Por terem massas diferentes, os pesos de cada bola serão diferentes. Logo, de acordo com a segunda lei de Newton, a força resultante sobre cada bola será diferente. Veja a imagem abaixo:

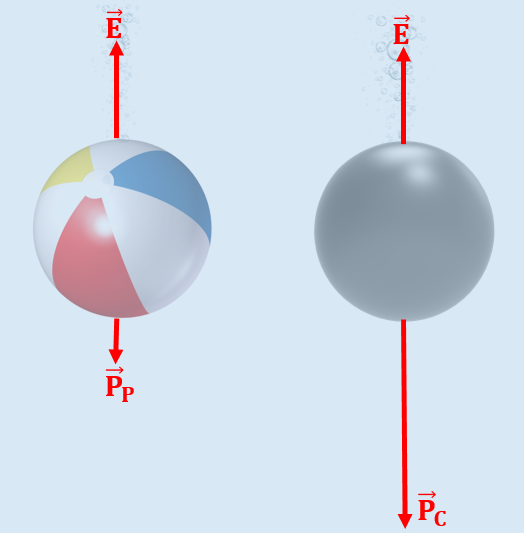
Os empuxos sobre cada bola são iguais, mas o empuxo é maior do que o peso da bola de praia, só que é menor do que o peso da bola de canhão. É por isso que, enquanto a de praia acelera para cima, a de canhão acelera para baixo.

⚠️ Tome cuidado para não confundir: quando a bola de praia chega à superfície, à medida em que sai, ela desloca quantidades cada vez menores de água. Como o empuxo depende dessa quantidade, então o empuxo reduz à medida em que a bola sai.

Chega um momento em que o empuxo é reduzido ao ponto de se igualar ao peso da bola. É nessa situação que ela entra em equilíbrio, flutuando na superfície.

Peso aparente

No caso das bolas na água, as únicas forças às quais elas foram submetidas são o peso e o empuxo. Para a bola de praia, o empuxo é maior do que o peso, então a o módulo da força resultante é dado por E - P. Já para a bola de canhão, o peso é maior do que o empuxo, então o módulo da força resultante é dado por P - E.

Se você estiver debaixo da água e tentar levantar a bola de canhão, vai perceber que ela parecerá muito mais leve do que realmente é! Afinal, o empuxo "alivia" o peso da bola de canhão. Essa diferença entre o peso e o empuxo é chamada de peso aparente. Não significa que seu peso tenha diminuído, apenas que ele é contrabalanceado pelo empuxo.

Caso coloque a bola de canhão em cima de uma balança debaixo da água, a balança não vai mostrar o valor verdadeiro da massa da bola, mas um valor reduzido, justamente porque a bola pressiona a balança com uma força de intensidade igual à de seu peso aparente (que é menor do que o peso real).

Empuxo na prática

Agora que aprendemos o que é empuxo e como ocorrem as situações de flutuação, podemos entender muito melhor diversas aplicações! Vamos conferir algumas?

Por que um navio flutua?

Apesar de serem extremamente pesados, os navios também têm volumes imensos, o que diminui sua densidade. Além disso, eles deslocam quantidades enormes de água, o que aumenta o empuxo sobre eles.

Para navegar em equilíbrio na superfície, um navio desloca uma quantidade de água cujo peso é igual ao seu (afinal, o peso da água deslocada é igual, em módulo, ao empuxo).

É por isso que um navio é capaz de flutuar, enquanto alguns parafusos afundam: mesmo que o navio e o parafuso sejam feitos do mesmo material, a densidade do parafuso faz com que ele afunde. Em outras palavras, ele não desloca uma quantidade suficiente de água para que o empuxo seja maior ou mesmo igual ao seu peso.

Icebergs

Os icebergs são imensos pedaços flutuantes de gelo. Como a densidade do gelo corresponde a aproximadamente 90% da densidade da água, um iceberg flutua na superfície, ao invés de afundar.

Além disso, devido a essa relação entre as densidades, cerca de 90% do iceberg se encontra submerso. É essa a porção de sua estrutura que desloca um volume de água cujo empuxo exercido tem o mesmo módulo de seu peso. Assim, o iceberg fica em equilíbrio na vertical.

Coletes salva-vidas

Quando vestimos um colete salva-vidas, conseguimos boiar mais facilmente na água. Isso acontece porque, considerando o nosso corpo e o colete, o volume aumenta, mas o peso aumenta numa proporção muito menor. Dessa forma, a densidade do sistema formado pelo nosso corpo e o colete é menor. Logo, o empuxo exercido é maior, fazendo a gente boiar.

Balões

Vimos vários exemplos envolvendo empuxo de líquidos, mas gases também exercem empuxo sobre corpos onde neles estejam imersos.

Um exemplo clássico são os balões de gás hélio: esse gás é menos denso do que o ar, sendo suficiente para que o peso de ar deslocado por um balão cheio de gás hélio (e, portanto, o empuxo exercido pelo ar) seja maior do que o peso do balão. Sendo assim, o empuxo é maior do que o peso, fazendo o balão subir.

Antigamente, o gás hidrogênio era utilizado em dirigíveis, o que provocava acidentes, visto que é inflamável.

Um outro exemplo, ainda mais antigo, mas também utilizado nos dias de hoje, é o dos balões de ar quente. Esses veículos conseguem voar porque, com o aquecimento do ar, se tornam menos densos do que o ar mais frio à sua volta. E os fluidos menos densos tendem a subir.

Resumo: empuxo

Veja os principais pontos sobre o assunto:

• Empuxo é uma força exercida por líquidos e gases (fluidos) sobre corpos que neles estejam imersos.
• O empuxo tem a direção vertical e o sentido de baixo para cima.
• O empuxo sobre um corpo imerso em um fluido é igual ao peso do fluido deslocado por esse corpo.
• A fórmula do empuxo pode ser descrita como E = mL · g, em que mL é a massa da porção deslocada de líquido ou gás.
• A fórmula do empuxo também é dada por E = dL · Vsub · g. Sendo: dL, a densidade do líquido; Vsub, o volume submerso do corpo; e g, a aceleração gravitacional.
• O que determina se um corpo afunda ou flutua é o seu peso e a forma como o peso se compara ao empuxo.
• Se o corpo flutua no líquido, a densidade do corpo é menor do que a densidade do líquido. Enquanto o corpo, inicialmente submerso, está subindo, o empuxo é maior do que o peso.
• Se o corpo afunda no líquido, a densidade do corpo é maior do que a densidade do líquido. O corpo afunda porque o peso é maior do que o empuxo.
• Se o corpo não flutua nem afunda no líquido, o corpo e o líquido têm a mesma densidade. O peso e o empuxo são iguais em módulo.

Como o empuxo cai no Enem e nos vestibulares

Após ter aprendido vários conceitos importantes e aplicações envolvendo empuxo, que tal aplicar esses conhecimentos em exercícios do Enem e dos vestibulares?

Exemplo 1

(Enem PPL 2016) Um navio petroleiro é capaz de transportar milhares de toneladas de carga. Neste caso, uma grande quantidade de massa consegue flutuar. Nesta situação, o empuxo é

a) maior que a força peso do petroleiro.

b) igual à força peso do petroleiro.

c) maior que a força peso da água deslocada.

d) igual à força peso do volume submerso do navio.

e) igual à massa da água deslocada.

Resposta: [B]
Para que o navio petroleiro seja capaz de flutuar em equilíbrio (sem afundar nem ser jogado para cima), é preciso que a força resultante sobre ele seja nula na direção vertical. Portanto, o empuxo sobre ele deve ser igual, em módulo, ao seu peso.
Não se esqueça: se o empuxo fosse maior do que o peso, então haveria uma força resultante para cima, fazendo com que o navio acelerasse nesse sentido.

Exemplo 2

(Enem 2010) Durante uma obra em um clube, um grupo de trabalhadores teve de remover uma escultura de ferro maciço colocada no fundo de uma piscina vazia. Cinco trabalhadores amarraram cordas à escultura e tentaram puxá-la para cima, sem sucesso.

Se a piscina for preenchida com água, ficará mais fácil para os trabalhadores removerem a escultura, pois a

a) escultura flutuará. Dessa forma, os homens não precisarão fazer força para remover a escultura do fundo.

b) escultura ficará com peso menor, Dessa forma, a intensidade da força necessária para elevar a escultura será menor.

c) água exercerá uma força na escultura proporcional a sua massa, e para cima. Esta força se somará á força que os trabalhadores fazem para anular a ação da força peso da escultura.

d) água exercerá uma força na escultura para baixo, e esta passará a receber uma força ascendente do piso da piscina. Esta força ajudará a anular a ação da força peso na escultura.

e) água exercerá uma força na escultura proporcional ao seu volume, e para cima. Esta força se somará à força que os trabalhadores fazem, podendo resultar em uma força ascendente maior que o peso da escultura.

Resposta: [E]
Com a piscina vazia, os trabalhadores precisarão exercer sobre a escultura uma força maior do que seu peso (podendo ser igual, em módulo, ao peso após começar a erguê-la). Ao encher a piscina, a escultura sofrerá ação do empuxo, que contribuirá com a força exercida pelos trabalhadores, facilitando o trabalho. Em outras palavras, o peso aparente da escultura será menor (mas o seu peso continua o mesmo, pois só depende da massa e da gravidade).
Além disso, de acordo com a fórmula que aprendemos (E = d_L · V_sub · g), o empuxo é proporcional ao volume da escultura, já que ela desloca um volume equivalente de água. O empuxo depende da densidade (e, portanto, da massa) de água, e não da escultura.

Exemplo 3

(Uerj 2016) Uma barca para transportar automóveis entre as margens de um rio, quando vazia, tem volume igual a 100 m³ e massa igual a 4,0x10⁴ kg. Considere que todos os automóveis transportados tenham a mesma massa de 1,5x10³ kg e que a densidade da água seja de 1000 kgxm^-3. O número máximo de automóveis que podem ser simultaneamente transportados pela barca corresponde a:

a) 10

b) 40

c) 80

d) 120

Resposta: [B]
A situação extrema é aquela em que todo o volume da barca (desconsiderando os volumes dos automóveis acima dela) está submersa. Essa é a situação em que a barca está na iminência de afundar. Nessa condição, o peso da barca (P_B) somado com o peso dos "n" automóveis (n · P_A) é igual, em módulo, ao empuxo (E):
P_B + n · P_A = E
Sendo M a massa da barca, m a massa de cada automóvel, g a aceleração gravitacional, d_ÁGUA a densidade da água e V o volume de água deslocada:
M · g + n · m · g = d_água · V · g
Simplificando os "g":
M + n · m = d_água · V
n = (d_água · V - M)/m = (1.000 · 100 - 4,0 · 10⁴)/1,5 · 10³ = (10⁵ - 4 · 10⁴)/1,5 · 10³
n = 6 · 10⁴/ 1,5 · 10³ = 40 automóveis