Produtos notáveis: como aplicá-los em problemas matemáticos?

No universo da Matemática, existem certas artimanhas que transformam a maneira como encaramos números e equações. Hoje, vamos destrinchar um desses tesouros: os produtos notáveis. Esses protagonistas da álgebra são poderosas ferramentas, prontas para simplificar expressões e resolver problemas com uma elegância satisfatória.

Imagine que, em vez de simplesmente resolver equações, você está decifrando códigos antigos ou tecendo uma tapeçaria complexa e intrínseca, onde cada fio é um número ou uma variável. Os produtos notáveis são as ferramentas que você usa para entrelaçar esses fios com maestria, criando padrões que revelam respostas de maneira surpreendentemente simples.

A seguir, vamos entender como eles funcionam e de que maneira podem ser aplicados em problemas matemáticos.

Produtos notáveis: o que são? Para que servem?

Produtos notáveis são expressões algébricas prontas, que surgem da multiplicação de binômios (expressões com dois termos) e outros polinômios. São como fórmulas mágicas que transformam multiplicações longas em um passe de mágica.

Os produtos notáveis possuem esse nome porque são expressões algébricas com propriedades específicas que facilitam cálculos e simplificações. Eles são "notáveis" por sua utilidade e por se destacarem pela frequência com que aparecem em problemas matemáticos.

Alguns dos produtos notáveis mais famosos são:

• Quadrado da soma de dois termos: \(\left(a+b\right)^2=a^2+2ab+b^2\)

• Quadrado da diferença de dois termos: \(\left(a-b\right)^2=a^2-2ab+b^2\)

• Produto da soma pela diferença de dois termos: \(\left(a+b\right)\left(a-b\right)=a^2-b^2\) 

Agora, você deve estar se perguntando: "Mas quando usar essas fórmulas?". Bem, os produtos notáveis têm várias utilidades, como:

1. Agilizar cálculos: eles fazem com que operações complexas fiquem mais tranquilas de serem resolvidas. Em vez de multiplicar termo por termo, você aplica a fórmula e o resultado aparece!
2. Resolver equações: em certas equações, aplicar um produto notável pode ser o truque que você precisa para encontrar a solução sem muitos problemas.
3. Simplificar expressões: eles ajudam a transformar expressões complicadas em formas mais simples, tornando a álgebra menos assustadora e mais amigável.
4. Entender conceitos avançados: no Ensino Superior, especialmente em cursos como Engenharia e Física, os produtos notáveis são os alicerces para compreender teorias mais complexas.

Conceitos iniciais de produtos notáveis

Produtos notáveis são expressões algébricas resultantes da multiplicação de polinômios que seguem certos padrões reconhecíveis, facilitando a resolução sem a necessidade de realizar toda a multiplicação termo a termo.

Dominar esses conceitos é como aprender os acordes de uma guitarra; de repente, você não está apenas tocando notas, mas sim, criando música com as fórmulas matemáticas.

Vamos descomplicar alguns conceitos referentes a este universo:

• ao falarmos sobre "quadrado", nos referimos à alguma base com expoente 2;
• quando o texto mencionar "cubo", nos referimos à alguma base com expoente 3;
• se for comentado sobre "soma", nos referimos à adição de dois ou mais fatores;
• caso a "diferença" apareça, trata-se da subtração de um fator pelo outro;
• ao discorrer sobre "produto", nos referimos à multiplicação de dois ou mais fatores.

👉 Leia também: Matemática básica: o que é, conteúdos e como estudar

Produtos notáveis e fatoração

Produtos notáveis são como as estrelas de um show matemático, oferecendo atalhos para multiplicar e manipular expressões algébricas com estilo e eficiência. Mas, assim como todo grande espetáculo, precisa de uma equipe nos bastidores.

A fatoração desempenha um papel crucial nos bastidores da álgebra, trabalhando em conjunto com os produtos notáveis para simplificar expressões e resolver equações.

Fator comum

Quando falamos de fator comum em Matemática, estamos frequentemente nos referindo ao maior divisor comum (MDC) ou ao fator comum mais básico em expressões algébricas.

Na aritmética, o MDC de dois ou mais números inteiros é o maior número inteiro que divide todos eles sem deixar resto. Por exemplo, o MDC de \(12\) e \(18\) é \(6\).

Esse conceito é fundamental na simplificação de frações, onde buscamos reduzir os termos ao mínimo, tornando a expressão mais elegante e manejável.

Na álgebra, encontrar o fator comum entre termos pode ser crucial para simplificar expressões e resolver equações.

Por exemplo, na expressão \(4x + 8\), o número 4 é um fator comum. Podemos "fatorar" esta expressão, o que significa tirar o fator comum e colocá-lo fora de um parêntese, resultando em \(4(x + 2)\), assim \(4x+8=4\left(x+2\right)\).

Isso simplifica a manipulação da expressão em equações ou funções mais complexas. Veja alguns exemplos da utilização de fator comum para modificar expressões:

• \(3x^3+18x^2+12x=3x\left(x^2+6x+4\right)\)

• \(2a^2x+ax^2=ax\left(2a+x\right)\)

• \(x^{2018}+x^{2021}=x^{2018}\left(1+x^3\right)\)

• \(5x^5-10a^2x^3-15a^3x^3=5x^3\left(x^2-2a^2-3a^3\right)\)

• \(\dfrac{1}{2}x^3+\dfrac{2}{4}x^2=\dfrac{1}{2}\left(x^3+\dfrac{1}{2}x^2\right)\)

Propriedades dos produtos notáveis

Quando se leva em conta o Triângulo de Pascal e os Binômios de Newton, existem diversas propriedades dos produtos notáveis. Entretanto, mostraremos as cinco principais:

Triângulo de Pascal e Binômios de Newton

O Triângulo de Pascal é uma disposição triangular dos coeficientes binomiais. Cada número é a soma dos dois números diretamente acima dele. Cada linha representa os coeficientes binomiais de uma expansão binomial.

Assim, a linha \(n\) contém os coeficientes dos termos na expansão de \((a+b)^n\). Veja sua representação visual:

Já os Binômios de Newton são expressões que surgem na expansão de potências de binômios, isto é, expressões da forma \((a+b)^n\). A Fórmula do Binômio de Newton é usada para encontrar essa expansão e se baseia nos coeficientes binomiais.

A fórmula geral é:

\((a+b)^n=\displaystyle\sum^n_{k=0}\dbinom{n}{k}a^{n-k}b^k\)

Quadrado da soma

Como o próprio nome já diz, é o quadrado da soma de alguma coisa, mais especificamente, é a soma de dois termos elevada ao quadrado.

\(\left(a+b\right)^2=a^2+2ab+b^2\)

Podemos observar tal propriedade utilizando recursos geométricos, em uma lógica de quebra-cabeça, no cálculo da área de um quadrado cujo o lado mede \(a+b\)

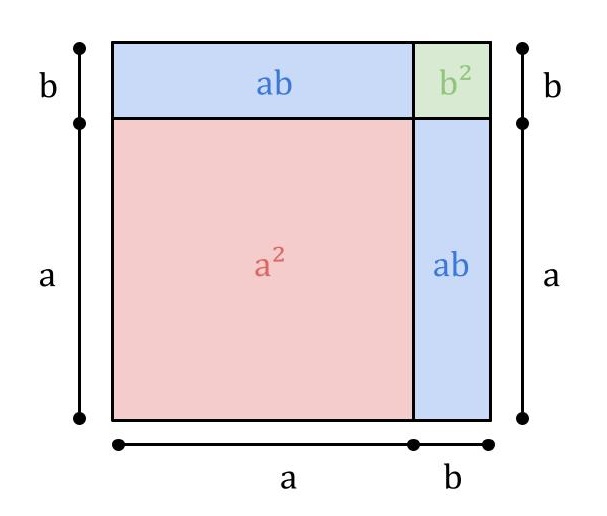
Observe que calcular a área do quadrado de lado \(\left(a+b\right)\) é equivalente a somar as áreas de cada figura do “quebra-cabeça” que mencionamos anteriormente. Assim, podemos escrever:

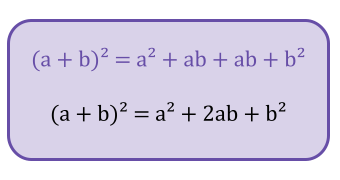
 Veja alguns de exemplos da utilização do quadrado da soma:

• \(\left(x+2\right)^2=x^2+4x+4\)
• \(\left(7x+4y\right)^2=49x^2+56xy+16y^2\)
• \(x^2+10x+25=x^2+2\cdot5x+5^2=\left(x+5\right)^2\)
• \(\left(\dfrac{1}{3}+4x\right)^2=\dfrac{1}{9}+\dfrac{8}{3}x+16x^2\)

Quadrado da diferença

Por outro lado, temos o quadrado da diferença, que, como o nome também nos diz, é o quadrado da diferença de dois termos. Ou seja, a diferença de dois termos elevada ao quadrado.

\(\left(a-b\right)^2=a^2-2ab+b^2\)

Podemos observar tal propriedade utilizando recursos geométricos no cálculo da área de um quadrado cujo lado mede \(a\) e subtraímos \(b\) de \(a\).

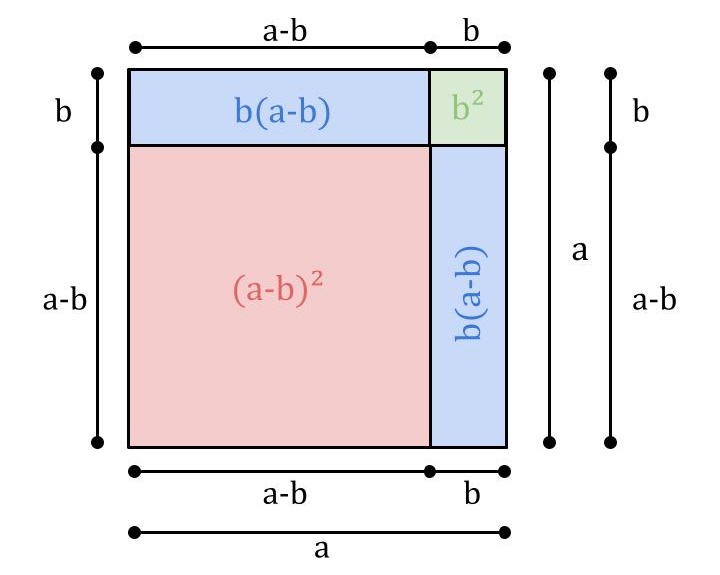
Observe que a soma de todas essas "peças" resulta em \(a^2\). Utilizando as manipulações algébricas e isolando o termo \((a-b)^2\), podemos chegar no resultado desejado:

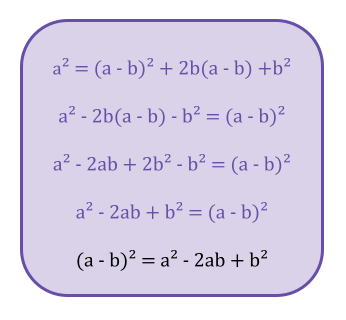
Veja alguns de exemplos da utilização do quadrado da diferença:

• \(\left(x-6\right)^2=x^2-12x+36\)
• \(\left(2x+3y\right)^2=4x^2+12xy+9y^2\)
• \(x^2-6x+9=x^2-2\cdot3x+3^2=\left(x-3\right)^2\)
• \(\left(\dfrac{1}{4}-3x\right)^2=\dfrac{1}{16}-\dfrac{3}{2}x+9x^2\)

Diferença de quadrados

A diferença de quadrados, de maneira análoga ao seu nome, é a subtração de dois termos que estão elevados ao quadrado. Sendo assim, ela é expressa pela forma: \(a^2 - b^2\).

⚠️ Importante: perceba que \(a^2 - b^2\neq \left(a-b\right)^2\).

A propósito, a diferença de quadrados é o resultado do produto entre a soma e a diferença de dois termos. Em consequência disso, temos que:

\(a^2-b^2=\left(a+b\right)\left(a-b\right)\)

Perceba que tal fato é verdade porque:

\(\left(a-b\right)\left(a+b\right)=a^2+ab-ba-b^2=a^2-b^2\)

Veja alguns de exemplos da utilização da diferença de quadrados:

• \(\left(x-3\right)\left(x+3\right)=x^2-3^2=x^2-9\)
• \(16x^2-49y^2=\left(4x-7y\right)\left(4x+7y\right)\)
• \(x^2-64=x^2-8^2=\left(x+8\right)\left(x-8\right)\)
• \(\dfrac{1}{4}x^2-\dfrac{1}{9}=\left(\dfrac{1}{2}x\right)^2-\left(\dfrac{1}{3}\right)^2=\left(\dfrac{1}{2}x-\dfrac{1}{3}\right)\left(\dfrac{1}{2}x+\dfrac{1}{3}\right)\)

Cubo da soma

O cubo da soma é análogo ao quadrado da soma. A diferença é que a soma dos dois termos é elevada ao cubo e não ao quadrado. Portanto, essa propriedade é da forma \(\left(a + b\right)^3\) ou \(\left(a + b\right)\cdot\left(a + b\right)\cdot\left(a + b\right)\).

Eventualmente, pela propriedade distributiva, temos que:

\(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)

Veja alguns exemplos da utilização do cubo da soma:

• \(\left(x+4\right)^3=x^3+12x^2+48x+64\)
• \(x^3+18x^2+108x+216=x^3+3\cdot x^2\cdot6+3\cdot x \cdot 6^2+6^2=\left(x+6\right)^3\)
• \(\left(6x+3y\right)^3=216x^3+324x^2y+162xy^2+27y^3\)
• \(\left(\dfrac{1}{2}+5x\right)^3=\dfrac{1}{2}+\dfrac{15}{4}x+\dfrac{75}{2}x^2+125x^3\)

Cubo da diferença

De forma adversa, o cubo da diferença é baseado no quadrado da diferença. Ocorre que a subtração entre os termos é elevada ao cubo, e não ao quadrado. Portanto, essa propriedade é da forma \(\left(a - b\right)^3\) ou \(\left(a - b\right)\cdot\left(a - b\right)\cdot\left(a - b\right)\).

Logo, utilizando a propriedade distributiva para desenvolver o cálculo, temos que:

\(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)

Veja alguns exemplos do cubo da diferença:

• \(\left(x-4\right)^3=x^3-12x^2+48x-64\)
• \(\left(5x-2y\right)^3=125x^3-150x^2y+60xy^2-8y^3\)
• \(x^3-9x^2+27x-27=x^3-3\cdot x^23+3\cdot x3^2-3^3=\left(x-3\right)^3\)
• \(\left(\dfrac{2}{3}+2x\right)^3=\dfrac{8}{27}+\dfrac{8}{3}x+8x^2+8x^3\)

👉 Leia também: Fórmulas matemáticas para Enem e vestibulares

Exercícios resolvidos: produtos notáveis

Agora que você aprendeu o que são os produtos notáveis e quais as suas propriedades, que tal conferir como podem aparecer nos processos seletivos?

O tema não é um dos mais cobrados nas provas dos vestibulares, mas, de vez em quando, pode aparecer. Assim, vale a pena conferir alguns modelos de exercícios de avaliações anteriores para entender de que forma o assunto pode surgir. Então, vamos conferir?

Exemplo 1

(IFSC 2018) Considere x o resultado da operação \(525^2-523^2\). Assinale a alternativa CORRETA, que representa a soma dos algarismos de x.

a) 18

b) 13

c) 02

d) 17

e) 04

Resposta [D]
\(x=525^2-523^2\)
\(x=\left(525-523\right)\cdot \left(525+523\right)\)
\(x=2\cdot 1048\)
\(x=2096\)
Portanto, a soma dos algarismos será: \(2 + 0 + 9 + 6 = 17\).  

Exemplo 2

(Uece 2022) O número irracional \(\left(\sqrt{2}-\sqrt{3}\right)^6\) é igual a

a) \(198−485\sqrt{6}\)

b) \(485−198\sqrt{6}\)

c) \(-198+485\sqrt{6}\)

d) \(-485+198\sqrt{6}\)

Resposta [B]
Tem-se que:
\(\left(\sqrt{2}-\sqrt{3}\right)^6=\left[\left(\sqrt{2}-\sqrt{2}\right)^2\right]^3\)
\(=\left[\left(\sqrt{2}\right)^2-2\cdot \sqrt{2}\cdot \sqrt{3}+\left(\sqrt{3}\right)^2\right]^3\)
\(=\left(5-2\sqrt{6}\right)^3\)
\(=5^3-3\cdot 5^2\cdot 2\sqrt{6}+3\cdot 5\cdot \left(2\sqrt{6}\right)^2-\left(2\sqrt{3}\right)^3\)
\(=485-198\sqrt{6}\)

🥇 Quer se preparar para o Enem e vestibulares com quem mais entende do assunto? A plataforma Aprova Total é a maior especialista no ensino digital e tem as melhores videoaulas e professores!