Campo elétrico e potencial elétrico: conceitos e aplicações

Campo elétrico e potencial elétrico são assuntos fundamentais para estudar tanto eletrostática quanto eletrodinâmica. Compreender bem o seu significado conceitual ajudará muito no entendimento dessas áreas da física. Veja o que são e o que têm a ver um com o outro.

Campo elétrico

Primeiramente, você já deve estar familiarizado(a) com cargas elétricas, certo? Sabemos que cargas de mesmo sinal se repelem e que cargas de sinais opostos se atraem. Podemos descrever matematicamente essas interações através da Lei de Coulomb, que nos diz como atua a força elétrica entre cargas.

A força elétrica é um tipo de força que atua à distância. Se lembra da força gravitacional? Ela é exercida entre dois corpos massivos, mesmo que esses não estejam em contato direto. Essa interação pode ser explicada pela presença de um campo gravitacional. Todo corpo massivo possui um campo gravitacional ao seu redor.

A ideia de campo elétrico é muito parecida com a de campo gravitacional. Toda carga elétrica (seja qual for o seu sinal) influencia o espaço à sua volta. É como se cada carga, simplesmente por existir, possuísse uma "aura" ao seu redor. Essa "aura" é o que chamamos de campo elétrico.

Por isso, ao aproximarmos uma carga de outra, estamos inserindo uma carga no campo elétrico da outra, fazendo com que elas interajam.

Que tipo de grandeza é um campo elétrico?

O campo elétrico é uma grandeza vetorial, ou seja, possui módulo, direção e sentido. Cada ponto de um campo elétrico tem sua representação vetorial, que indica o vetor campo elétrico nesse mesmo ponto.

Por ser um vetor, precisamos ilustrar todos os três parâmetros do campo elétrico. Para isso, costumamos utilizar linhas de campo, que são linhas imaginárias responsáveis por indicar, ponto a ponto, o módulo e a orientação desse vetor.

O vetor campo elétrico é sempre tangente à linha de campo em cada ponto e aponta no mesmo sentido delas. Por convenção, as linhas apontam "para dentro" de cargas negativas e "para fora" de cargas positivas:

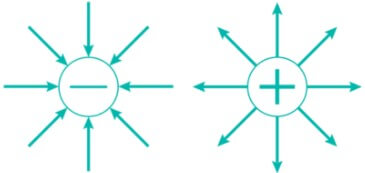
Através das linhas de campo, podemos verificar onde o campo elétrico é mais intenso: onde há uma maior densidade de linhas, ou seja, onde as linhas de campo estão mais próximas umas das outras.

Campo elétrico uniforme

De acordo com o que vimos, podemos também definir um campo elétrico uniforme: esse tipo de campo possui mesmo módulo e mesma orientação em cada região do espaço.

Veja que, na imagem abaixo, as linhas de campo saem de uma placa (positivamente carregada) e entram em outra placa (negativamente carregada). Essas linhas estão igualmente espaçadas e têm o mesmo tamanho, o que caracteriza um campo elétrico uniforme.

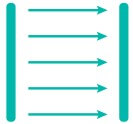
Como calcular o módulo de um campo elétrico?

Podemos calcular o módulo de um campo elétrico (E) de duas formas, que são equivalentes:

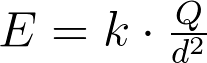
em que:

k é a constante eletrostática (aquela mesma da Lei de Coulomb);

Q é o módulo da carga geradora do campo elétrico;

d é a distância entre a carga geradora e o ponto onde estamos calculando o campo.

A outra forma de calcular o módulo do campo em um ponto de sua região consiste em adicionar uma outra carga (q) sobre esse ponto:

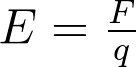
em que F é o módulo da força elétrica entre Q e q.

Mas quando utilizar cada uma das equações? Isso depende das informações que temos para resolver a questão.

Caso saibamos o módulo da carga geradora e a distância ao ponto onde queremos calcular o módulo do campo, utilizamos a primeira equação.

Se temos uma carga de prova e podemos calcular a força elétrica entre essa carga e a carga geradora, é conveniente utilizar a segunda equação.

De acordo com o Sistema Internacional (SI), a unidade de campo elétrico é newton por coulomb (N/C), que é equivalente a volt por metro (V/m).

Blindagem eletrostática

Você sabia que um dos lugares mais seguros para se proteger de raios é dentro de um carro?

Se considerarmos um objeto cuja superfície externa é feita de um material condutor (metal, por exemplo), os elétrons sobre essa superfície se repelem de maneira que a distribuição de cargas torne nulo o campo elétrico em seu interior. Esse fenômeno é conhecido como blindagem eletrostática.

Um objeto ou lugar que possua blindagem eletrostática é conhecido como gaiola de Faraday, uma referência ao experimento do cientista britânico Michael Faraday.

Potencial elétrico

Toda carga elétrica localizada no interior de um campo elétrico possui uma energia potencial elétrica (E_p) associada à sua posição dentro desse campo.

Se considerarmos algum ponto dentro de um campo elétrico, podemos calcular a quantidade de energia que um coulomb de carga pode armazenar nesse ponto.

Dessa forma, temos outra grandeza física: o potencial elétrico (V), que pode ser calculado da seguinte forma:

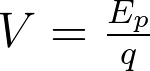
Também podemos calcular o potencial elétrico através da carga geradora (Q) e de sua distância (d) até o ponto onde estamos calculando o potencial:

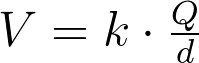
novamente, k é a constante eletrostática. Ambas as equações são equivalentes, apenas formas diferentes de dizer a mesma coisa.

O potencial elétrico é uma grandeza escalar, cuja unidade no SI é joule por coulomb (J/C), também conhecida como volt (V).

Diferença de potencial

Logo após termos definido potencial elétrico, podemos falar de diferença de potencial (ddp). Também chamada de tensão, ou ainda, informalmente, de voltagem, essa grandeza corresponde à diferença dos potenciais elétricos entre dois pontos.

Sem dúvida, a ddp é uma das grandezas mais importantes nos estudos de eletricidade. Afinal, é a existência de uma diferença de potencial que proporciona um fluxo ordenado de cargas, a famosa corrente elétrica, que é muito utilizada em eletrodinâmica.

A ddp também possui sua grandeza no SI: o volt (V).

Diferenças de potenciais são responsáveis por diversos fenômenos, como os raios: quando há uma grande diferença de potencial entre as nuvens e a superfície da Terra, podem ocorrer descargas elétricas.

Superfícies equipotenciais

Agora que sabemos o que é potencial elétrico (assim como uma diferença de potencial), podemos falar de superfícies equipotenciais.

Essas superfícies imaginárias são assim denominadas porque todos os pontos que as constituem apresentam o mesmo potencial elétrico. Dessa forma, dois pontos quaisquer que estejam em uma superfície equipotencial não têm diferença de potencial entre eles.

Se considerarmos, por exemplo, uma carga pontual, suas superfícies equipotenciais são cascas esféricas cuja origem é a própria carga. Isso é representado (de forma 2D) na figura abaixo:

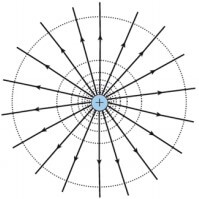
É importante ressaltar que as linhas de campo são sempre normais (ou seja, formam 90º) às superfícies equipotenciais. Além disso, o potencial elétrico decresce no sentido das linhas de campo. Isso significa, por exemplo, que se seguirmos no sentido "para fora" da imagem acima, estamos seguindo o sentido das linhas de campo e, portanto, o potencial elétrico está diminuindo.

🥇 Quer preparação máxima para ter alto rendimento no Enem e ingressar no curso dos seus sonhos? 
Então conheça a plataforma do Aprova Total!